Жолобов Ввведение в Математическое 2008

2.4.3. Метод Лэнд и Дойг

Дана задача линейного частично-целочисленного программирования:

Тот факт, что (2.32)-(2.34) – задача линейного программирования, сразу наталкивает на мысль, что границу (верхнюю) удобнее всего вычислять, решая именно эту задачу. Действительно, ведь всегда имеет место

Z1,2,3opt Z1,2,3,4opt .

Вопрос вычисления границы решен.

Как будем выполнять ветвление и какой признак оптимальности – станет ясно в процессе изложения алгоритма.

Рекордом будем называть допустимое решение задачи ЛЦП, доставляющее ЦФ значение, не меньшее, чем на любом известном на данный момент допустимом решении.

Шаг 1. Решим задачу ЛП (2.32)-(2.34). Если задача неразрешима, то и ЛЦП-задача (2.32)-(2.35) неразрешима. Полагаем N=1 и в предварительно очищенный список задач S заносим задачу ЛП

(2.32)-(2.35), дав ей обозначение З1 . В этот же список заносим оптимальное решение задачи, которое принимается в качестве верхней границы 1 .

Шаг 2. Имеем список задач S, в котором задачи упорядочены по невозрастанию оценок:

S {З1 ( 1 ), З2 ( 2 ), ... , ЗN ( N )}.

Если список пуст (S= ), ЛЦП-задача не имеет решения. Ко-

нец.

291

В противном случае из списка выбирается задача З1 – задача, имеющая максимальную оценку.

Шаг 3. Если оптимальный план выбранной задачи X1 удовлетворяет требованию целочисленности (2.35), то X1 – оптимальное решение исходной задачи, 1 – оптимальное значение ЦФ. Конец.

Шаг 4. Выбираем нецелую координату решения X1 . Пусть это бу-

По результатам решения каждой из задач З11 и З12 выполня-

ются следующие действия.

Если задача имеет решение, то она вместе со своим оптимальным решением заносится в список задач S – в позицию, соответствующую полученному значению ЦФ (оценки). Таким образом, все задачи в новом списке S' упорядочиваются по невозрастанию оценок.

Шаг 5. Проводится сквозная перенумерация задач в новом списке. Этот список приобретает вид:

S {З1 ( 1 ), З2 ( 2 ), ..., Зl ( l ),..., ЗN ' ( N ' )}1 2 ... l ... N ' .

Из списка удаляются все бесперспективные задачи. Задача Зr считается бесперспективной, если в списке есть задача Зl , имеющая целочисленное решение и r > l , т.е., l r . Таким образом, срабатывает механизм рекордов. А именно, задача Зl , имеющая

целочисленное решение (если таковая есть), в новом списке будет занимать последнюю позицию. Этой задаче будет соответствовать рекорд.

В новом, очищенном от бесперспективных задач списке будет N задач (N N'). Принимаем S= S' и переходим к шагу 2.

292

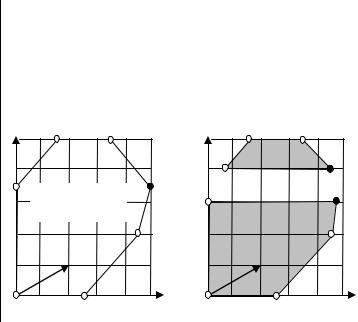
З1:

1=131/2; X1=(5, 7/2)

2.4.4. Использование штрафов в методе Лэнд и Дойг

Допустим, решена некоторая задача из списка задач, и получено нецелочисленное решение этой задачи.

Оптимальная симплекс-таблица имеет вид (рис. 2.24):

Рис.2.24. Оптимальная симплекс-таблица

Пусть xp0 – значение некоторой базисной переменной xp в оптимальном решении, не удовлетворяющее требованию целочис-

294

ленности. Для определенности примем, что p {1,2,...,m}; а xj , где j {m+1,m+2,...,n} – небазисные переменные.

В p-й строке последней симплекс-таблицы записано следующее уравнение:

j m 1

Что означает ветвление по переменной xp ?

Это означает, что необходимо сформировать две новые задачи, в систему ограничений одной из которых должно войти огра-

ничение xp [xp0 ] + 1.

В систему ограничений другой задачи должно войти ограни-

чение xp [xp0 ] (рис. 2.25).

Рис.2.25. Задачи, получаемые при ветвлении

Случай А. Переменная xp должна принять значение, не меньшее, чем [xp0 ] + 1. Следовательно, эта переменная должна быть увеличена, по крайней мере, на величину:

1 - { xp0}.

Как поведут себя свободные переменные?

n

xp= xp0 - xpj x j . j m 1

По крайней мере, одна из этих переменных (пусть это будет xj, для которой xpj < 0) должна увеличиться на некоторую величину

, которую можно найти из уравнения (2.36):

xp+(1 - { xp0})= xp0 - xpj(0 + ).

Здесь "0" – старое значение xj ; " " – новое значение. Ввиду того, что xp= xp0 , имеет место

295

1 - { xp0}= - xpj

Отсюда определяется :

= 1 {xp0 }

xpj

В разделе 1.2.15 было показано, что оценки свободных переменных – это взятые с обратным знаком коэффициенты, с которыми свободные переменные входят в целевую функцию, если базисные переменные выразить через свободные. То есть, справедливо следующее выражение:

меняют своих значений – остаются нулевыми. Следовательно, це-

ним, что xpj < 0, а все j 0 ).

Теперь можно сделать вывод о том, что минимальная величина, на которую должно уменьшиться (ухудшиться) значение целе-

вой функции в результате наложения ограничения xp [xp0 ] + 1, определяется следующим образом:

Эту величину принято называть штрафом сверху.

Следует подчеркнуть важное обстоятельство: для определения этого штрафа задачу можно не решать.

Всегда ли можно вычислить штраф сверху? Нет, не всегда. Действительно, может оказаться, что p-я строка симплекс-таблицы не имеет ни одной отрицательной координаты xpj < 0.

n

Вернемся к выражению xp= xp0 - xpj x j . Ограничение

j m 1

xp [xp0 ] + 1 эквивалентно следующему ограничению: 296

j m 1

т.е.

n

xpj x j -1+ { xp0}.

j m 1

Для того чтобы работать по симплекс-методу, это ограничение нужно привести к виду уравнения путем введения дополни-

тельной переменной yp 0. Соответствующая строка симплекстаблицы будет иметь вид:

Левая часть этого уравнения – отрицательное число. Оценки остались неотрицательными. То есть теперь в симплекс-таблице записан псевдоплан: нужно работать по двойственному симплексметоду. В столбце A0 есть единственный отрицательный элемент (-1+ { xp0} ), но в соответствующей этому элементу строке нет ни одной отрицательной координаты.

Это – тот случай, когда в двойственном симплекс-методе срабатывает признак недопустимости задачи.

Таким образом, если штраф сверху не удается найти, соответствующую задачу можно не решать – она недопустима.

Случай Б. Переменная xp должна принять значение, не большее, чем [xp0 ] . Следовательно, эта переменная должна быть уменьшена, по крайней мере, на величину {xp0}.

Как "поведут себя" свободные переменные?

n

xp= xp0 - xpj x j j m 1

Эти переменные могут только увеличиваться. По крайней мере, одна из этих переменных (пусть это будет xj ), для которой

xpj > 0 , должна увеличиться на некоторую величину . Эту величину можно найти из уравнения (2.36):

xp - { xp0}= xp0 - xpj(0 + ).

Здесь "0" – старое значение xj ; " " – новое значение. 297

Ввиду того, что xp= xp0 , имеет место:

- { xp0}= - xpj .

Отсюда определяется :

Пусть при этом остальные свободные переменные не изменяют своих значений – остаются нулевыми. Следовательно, целевая

xpj > 0).

Теперь можно сделать вывод о том, что минимальная величина, на которую должно уменьшиться (ухудшиться) значение целе-

Эту величину принято называть штрафом снизу.

Так же, как и в предыдущем случае, для определения штрафа снизу задачу можно не решать.

Всегда ли можно вычислить штраф снизу? Нет, не всегда. Действительно, может оказаться, что p-я строка симплекс-таблицы не имеет ни одной положительной координаты xpj > 0.

n

Вернемся к выражению xp= xp0 - xpj x j . Ограничение

j m 1

xp [xp0 ] эквивалентно следующему ограничению:

n

xp0 - xpj x j [xp0 ].

j m 1

298

j m 1

Для того чтобы работать по симплекс-методу, это ограничение нужно привести к виду уравнения путем введения дополнительной переменной yp 0. Соответствующая строка симплекстаблицы будет иметь вид:

Левая часть этого уравнения – отрицательное число. Оценки остались неотрицательными. То есть теперь в симплекс-таблице записан псевдоплан: нужно работать по двойственному симплексметоду. В столбце A0 есть единственный отрицательный элемент (- { xp0} ), но в соответствующей этому элементу строке нет ни од-

ной отрицательной координаты (так как все xpj 0).

В двойственном симплекс-методе срабатывает признак недопустимости задачи.

Таким образом, если штраф снизу не удается найти, соответствующую задачу можно не решать – она недопустима.

Итак, мы только что сформулировали правила, по которым можно отбрасывать ветви, соответствующие задачам, не имеющим решения. Очень важно, что использование механизма штрафов позволяет вообще отказаться от решения соответствующих задач.

Следующий вопрос – это использование механизма штрафов для отсеивания бесперспективных ветвей.

Допустим, в результате решения серии задач ЛП в списке задач имеется некоторая задача, оптимальное решение которой удовлетворяет требованию целочисленности, и на этом решении целевая функция имеет значение R.

Пусть из списка выбирается некоторая задача, имеющая максимальную оценку Z* (естественно, большую, чем R).

Пусть далее выбирается нецелая координата xp , и по этой координате вычисляются штрафы. Если какой-либо штраф не удается вычислить, соответствующая ветвь отбрасывается, так как новая задача не имеет решения.

299

Пусть вычислены штрафы ZUp (сверху) и Z Dp (снизу).

Тогда открывается возможность установить "бесперспективность" соответствующих новых задач:

1. Z* - ZUp R – решать задачу, которая порождается введением

ограничения xp [xp0 ] + 1 не имеет смысла: оценка будет заведомо плохой;

2. Z* - Z Dp R – решать задачу, которая порождается введением

ограничения xp [xp0 ] не имеет смысла: оценка будет заведомо плохой.

Отсюда естественным образом вытекает следующее правило: если max{ Z* - ZUp , Z* - Z Dp } R , следует вообще отказать-

ся от ветвления по переменной xp (соответствующая ветвь просто отбрасывается).

Ветвление имеет смысл осуществлять по той переменной, которая имеет максимальный штраф.

Штраф переменной xp (p=1,2,...,m) определяется следующим образом:

Z p = max{ ZUp , Z Dp }.

Таким образом, для ветвления выбирается переменная с максимальным штрафом – ускоряется процесс уточнения оценки.

После того, как выбрана переменная, формируются две зада-

чи.

Впервую очередь решается та задача, которая обладает минимальным штрафом (сверху или снизу).

Эта задача, если, конечно, она перспективна, решается и помещается в список.

Затем исследуется вторая задача (если она есть). Если она перспективна (первая решенная задача может сделать вторую бесперспективной), то решается и помещается в список задач.

Вобщем случае перспективность той или иной задачи проверяется два раза: до и после решения.

Взаключение этого раздела о приближенном решении задач

ЛЦП методом Лэнд и Дойг.

Предположим, что Vк – это максимальная верхняя граница, известная к шагу k работы алгоритма.

300