Жолобов Ввведение в Математическое 2008

2.2.13. Дополнительные ограничения в постановке транспортной задачи

При постановке и нахождении решения конкретных транспортных задач часто бывает необходимо учитывать дополнительные ограничения, которые еще не рассматривались.

261

Рассмотрим подробно некоторые из таких ограничений.

1. Запрещена перевозка из пункта Ai в пункт Bj . В этом случае вводится очень высокий тариф (М) перевозки из пункта Ai в пункт Bj единицы продукции:

cij=M .

2. Из пункта Ai в пункт Bj требуется обязательно перевести точно dij единиц продукции. В клетку на пересечении i-й строки и j-го столбца вносится величина dij. Корректируется запас ai и потреб-

ность bj : ai ai dij , bj bj dij . В дальнейшем эта клетка счита-

ется свободной, а для того чтобы соответствующая переменная не попала в состав базисных переменных оптимального решения, этой клетке приписывается очень большой тариф: cij=M .

3. Из пункта Ai в пункт Bj требуется перевести не менее ij единиц продукции. Считаем, что из пункта Ai в пункт Bj уже перевезено ij единиц продукции. Уменьшаем запас ai и потребность bj на ве-

обычным методом, после чего корректируется полученное решение. Смысл этой корректировки заключается в следующем. Если в

оптимальном решении переменная xij принимает значение xij , то в окончательном решении ей приписывается значение xij xij ij .

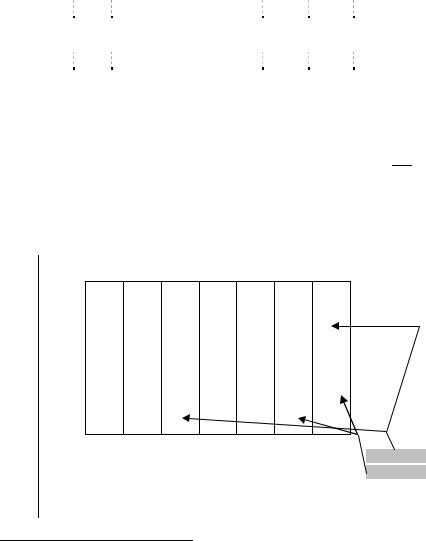
4. Из пункта Ai в пункт Bj требуется перевести не более ij единиц продукции. В исходную таблицу вводится дополнительный

столбец Bj (рис. 2.11):

262

Рис.2.11. Моделирование дополнительного ограничения

В окончательном решении принимается xij xij xij , i 1, m .

Естественно, что открывается возможность комбинировать

эти приемы и решать задачи с достаточно «серьезными» ограничениями20.

Пример 2.12

Построить транспортную модель с дополнительными ограничениями.

Дополнительные ограничения:

Из A1 в B2 должно быть перевезено не менее 50 ед. (x12 50); Из A3 в B5 должно быть перевезено не менее 60 ед. (x35 60); Из A2 в B4 должно быть перевезено не более 40 ед. (x24 40).

Учтем теперь ограничение x24 40. Для этого нужно ввести но-

20 В частности, достаточно просто учитывается ограничение dн xij dв.

263

Теперь обычным способом решаем эту задачу (находим исходное опорное решение, а далее, например, используем метод потенциалов).

Однако помним, что полученные значения x12 и x35 нужно будет увеличить соответственно на 50 и 60 единиц.

2.2.14. Транспортная модель с промежуточными пунктами

Транспортная модель с промежуточными пунктами соответствует реальной ситуации, когда между исходными и конечными пунктами перевозок имеются промежуточные пункты для временного хранения грузов (транзитные пункты). Это – более общая, чем обычная транспортная модель, где перевозки осуществляются непосредственно между пунктами отправления и назначения.

Проведем сквозную нумерацию всех пунктов (исходных, ко-

нечных, транзитных): 1, 2,…, R.

Транспортную модель представим орграфом, вершинам которого соответствуют пункты 1, 2,…, R.

В том случае, если существует возможность перевозки про-

сk,l

Рис.2.12. Дуга между промежуточными пунктами

264

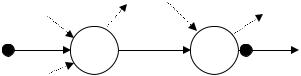
Модель предполагает возможность сосредоточения запасов продукции в любом пункте. Кроме того, каждый пункт может иметь собственную потребность в определенном количестве продукции. Этот факт будем отображать на графе следующим образом

(рис. 2.13):

Рис.2.13. Запасы и потребности в модели

Здесь ak – количество единиц продукции, сосредоточенной в пункте k ; bl – количество единиц продукции, составляющее по-

требность пункта l .

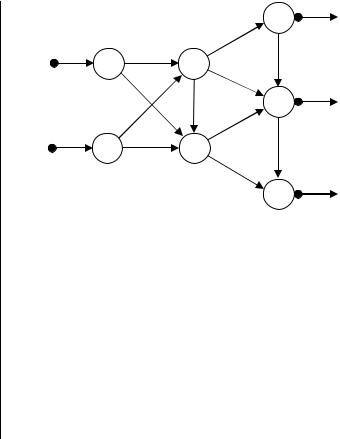
В рассматриваемой модели перевозки транзитом могут осуществляться через любые пункты (в соответствии с направлением взвешенных дуг на орграфе), даже через некоторые пункты назначения.

Поэтому все множество пунктов 1, 2,…, R можно разбить на три класса.

1.Пункты, которым соответствуют как входящие, так и исходящие взвешенные дуги, назовем транзитными пунктами (ТП).

2.Пункты, которым соответствуют только исходящие взвешенные дуги, назовем истинными пунктами отправления (ИПО).

3.Пункты, которым соответствуют только входящие взвешенные дуги, назовем истинными пунктами назначения (ИПН).

Представленную таким орграфом транспортную модель с промежуточными пунктами преобразуем в обычную (закрытую) транспортную модель с помощью введения, т.н. буфера.

Объем буфера (B) должен быть таким, чтобы вместить объем всего предложения (или спроса):

B = Общий объем предложения (спроса).

Объемы спроса (предложения) перечисленных выше трех подмножеств пунктов определяются следующим образом:

объем предложения ИПО = объем исходного предложения;

объем спроса ИПН = объем исходного спроса;

объем предложения ТП = объем исходного предложения + B;

265

объем спроса ТП = объем исходного спроса + B.

При построении закрытой транспортной модели в качестве поставщиков принимаются все ИПО и все ТП. В качестве потребителей – все ТП и все ИПН.

Для того чтобы запретить перевозки между пунктами, не связанными в исходном орграфе взвешенными дугами, соответствующим маршрутам (запрещенным), приписывается достаточно высокая стоимость (M). Маршрутам, соответствующим петлям (из одного ТП в тот же самый ТП) приписывается нулевая стоимость.

Ниже рассматривается пример решения транспортной задачи с промежуточными пунктами.

Пример 2.13

Здесь P1 и P2 – ИПО; T1, T2, T3, T4 – ТП; D1 – ИПН.

B = 1000+1200=800+900+500=2200.

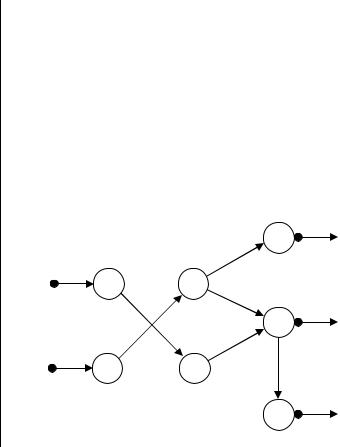
Строим транспортную таблицу и решаем задачу:

266

Контрольные вопросы и задачи к разделу 2.2

1.Сравните метод Фогеля и метод плавающих зон с точки зрения вычислительных затрат на решение задачи и степени приближенности получаемого приближенного решения к оптимальному.

2.Дана транспортная задача. Эта задача решается методом Фогеля.

Имеем значение ЦФ Zисх. Введем в эту задачу дополнительное ограничение (например, запретим какой-либо маршрут). Получим значение ЦФ Zдоп. Можно ли утверждать следующее и почему:

а)Zисх Zдоп б)Zисх Zдоп?

267

3.Возможен ли в методе потенциалов случай зацикливания, аналогичный тому, который возможен в симплекс-методе в случае вырожденности задачи?

4.Докажите утверждение, что косвенная стоимость – это коэффициент, с которым свободная переменная входит в целевую функцию, если все базисные переменные выразить через свободные.

5.Каким образом можно привести открытую транспортную задачу с промежуточными пунктами к закрытой?

6.Решите задачи методами северо-западного угла, наименьшей стоимости, Фогеля и методом плавающих зон:

7. В процессе решения задачи с помощью метода потенциалов была получена следующая транспортная таблица:

Продолжите решение задачи.

8. Решите задачу распределительным методом, применив метод наименьшей стоимости для поиска исходного опороного решения:

ниц продукции.

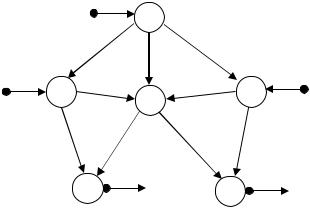
10. Решите транспортную задачу с промежуточными пунктами:

269

2.3. Метод отсечения

2.3.1.Основные понятия метода отсечения

Всвоей основе метод отсечения использует тот факт, что, если все вершины многогранного множества D имеют целочисленные координаты, то и оптимальное опорное решение соответствующей задачи ЛП будет удовлетворять требованию целочисленности.

Рассмотрим ЛЦП-задачу:

Допустимое множество этой задачи, определенное ограниче-

ниями (2.24)-(2.26), обозначим Dц.

Очевидно, Dц – множество целых точек выпуклого многогранного множества D, определенного ограничениями (2.24)-(2.25).

С целью упрощения последующих выкладок будем считать, что D – замкнутое ограниченное множество. То есть Dц – конечное множество.

Обозначим Dц* выпуклую линейную оболочку множества Dц.