Жолобов Ввведение в Математическое 2008

2.Рассчитайте координаты точки, вокруг которой вращается линия уровня в задаче дробно-линейного программирования со свободными членами.

3.Решите задачу дробно-линейного программирования

4x1 6x2 max

x1 2x2

3x1+2x2≤37

4x1+3x2≤51

x1≥5 x2≥5

x1,2 0.

4. Решите задачу дробно-линейного программирования со свободными членами

3x1 2x2 1 max x1 x2 2

4x1+3x2≤8 -2x1+5x2≤9

x1,2 0.

1.6. Квадратичное программирование

1.6.1. Метод множителей Лагранжа

Метод Лагранжа является наиболее распространенным методом решения нелинейных оптимизационных задач с ограничениями в виде уравнений:

При этом делается допущение о дифференцируемости всех

функций f (x1,..., xn ) , gi (x1,..., xn ) .

Метод основан на построении функции Лагранжа вида

Тогда показано, что существует такой вектор * ( 1* ,..., m* ) , что

191

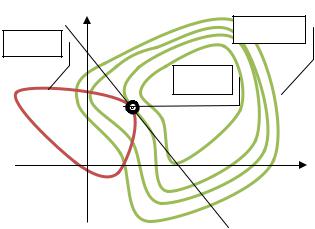
Пусть уравнение g(x1, x2 ) 0 задает в пространстве гладкую кривую (рис.1.30).

x2

f (x1, x2 )

g(x1, x2 )

(x1* , x2* )

x1

Рис.1.30. Геометрическая интерпретация метода множителей Лагранжа

Из геометрических соображений очевидно, что оптимальное решение задачи (x1* , x2* ) может быть расположено только в точке

касания кривой g(x1 , x2 ) 0 и какой-либо линии уровня целевой функции f (x1, x2 ) h , поскольку в бесконечно малой окрестности

любой точки пересечения (но не касания) этих двух кривых можно найти точки как превышающие значение h, так и меньшие этого значения. Поскольку для каждой точки в пространстве градиент произвольной функции (x1, x2 ) перпендикулярен касательной к

Шаг 1. Построить функцию Лагранжа (1.121):

m

L(x1,.., xn , 1,..., m ) f (x1,.., xn ) i gi (x1,.., xn ) .

i 1

Шаг 2. Вычислить градиент функции (первые частные производ-

Шаг 3. Приравнять нулю все элементы градиента функции Лагранжа, решить систему из m+n уравнений с m+n неизвестными из

Шаг 4. Исследовать стационарные точки – решения системы уравнений (1.128). Поскольку мы предположили, что имеем дело с задачей, для которой условие (1.122) является достаточным условием оптимальности решения, полученные решения системы (1.128) являются оптимальными решениями исходной задачи (1.120).

1.6.2. Элементы теории выпуклого программирования

Для обоснования аппарата выпуклого программирования нам понадобятся некоторые элементы линейной алгебры, которые для справки приведены в этом разделе.

Функция f(X) называется строго выпуклой, если для любых двух различных точек X1 и X2 выполняется неравенство:

194

Для того чтобы определить тип квадратичной формы, используются необходимые и достаточные условия, которые определяются следующими утверждениями.

Квадратичная форма Q(X) будет положительно определенной (положительно полуопределенной), если значения всех угловых миноров определителя |D| положительны (неотрицательны). В этом случае матрица D называется положительно определенной (полуопределенной).

Квадратичная форма Q(X) будет отрицательно определенной, если значения k-х угловых миноров определителя |D| отличны от нуля и имеют знак (-1)k, k=1, 2, … , n. В этом случае матрица D называется отрицательно определенной.

То есть матрица D отрицательно определенная и, соответственно, функция Q(X) является строго вогнутой.

196

То есть матрица D отрицательно полуопределенная и соответственно, функция Q(X) является нестрого вогнутой.

1.6.3. Выпуклый анализ, условия Куна-Такера

Дана задача нелинейного программирования

Задача (1.129) относится к классу задач выпуклого программирования, если z является вогнутой (выпуклой) функцией, а область допустимых решений, которая определяется ограничениями gi(x1, x2, … , xn) 0 (i =1, 2, … , m), представляет собой выпуклое множество.

Важнейшее свойство задач выпуклого программирования заключается в том, что любая экстремальная точка является точкой глобального экстремума.

Рассмотрим геометрическую интерпретацию задачи выпуклого программирования. Пусть в задаче (1) n=2 и m=3.

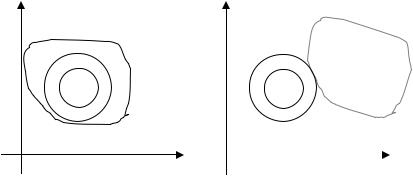
Обозначим X' = (x'1, x'2) – точку максимума целевой функции в задаче без ограничений, X'' = (x''1, x''2) – точку условного максимума целевой функции (оптимальное решение задачи (1.129)). На рис. 1.31 представлены возможные случаи решения задачи. Пунктирные линии – линии уровня, на которых ЦФ принимает одно и то же значение.

197

Рис.1.31. Случаи решения задачи выпуклого программирования

Перепишем теперь задачу в матрично-векторной форме: z = f(XT) max

G(X) 0,

где X = (x1, x2, … , xn)T , G(X) = (g1(X), g2(X), … , gm(X))T.

От ограничений-неравенств перейдем к ограничениям-

В задаче максимизации (минимизации) необходимым условием оптимальности является неотрицательность (неположитель-

ность) множителей . Остальные условия формулируются следующим образом.

Рассмотрим условия (1.131):

s1

T S =( 1, 2, … , m) s2 = ( 1s1, 2s2, … , msm) = (0, 0, … , 0)

sm

Условия (1.133) можно интерпретировать следующим обра-

зом.

Если i 0, то si = 0. То есть, ограничение gi(X) 0 должно обращаться в строгое равенство (gi(X) = 0).

Если si 0, то i = 0 . При этом ограничение gi(X) 0 должно обращаться в строгое неравенство (gi(X) < 0).

Таким образом, условия фактически эквивалентны следующим условиям:

Учитывая условия (1.134) и приведенную выше интерпретацию условий (1.133), условия (1.132) можно заменить условиями

G(X) 0.

199

Теперь для задачи максимизации можно сформулировать условия Куна-Таккера, необходимые для того, чтобы векторы

X и определяли стационарную точку:

Для задачи выпуклого программирования необходимые условия Куна-Таккера являются также и достаточными условиями. Этот факт используется при решении задач квадратичного программирования.

1.6.4. Сведение задачи квадратичного программирования к задаче линейного программирования

Задачи квадратичного программирования часто встречаются в экспериментальной физике, в том числе в той её области, которая связана с ядерными исследованиями. Это обусловлено формулой оценки ошибки в экспериментальных данных как суммы квадратов отклонений измеряемой величины от среднего. Как правило, условия проведения эксперимента и последующие вычисления строятся таким образом, чтобы минимизировать ошибку, что позволяет явным образом сформулировать оптимизационную задачу, в которой целевая функция имеет вид квадратичной формы. Классическим примером широкого применения задачи квадратичного программирования (без ограничений) в эксперименте является известный метод наименьших квадратов [3]. Далее в пособии будет рассматриваться методика решения подобных задач в условиях существования линейных ограничений на допустимую область задачи.

Задача квадратичного программирования имеет следующий

вид:

где

200