
Жолобов Ввведение в Математическое 2008
.pdf
Частный случай определения исходного псевдоплана
В отдельных случаях исходный псевдоплан непосредственно определяется из исходной задачи, если она имеет специальную структуру.
Пусть требуется решить задачу ЛП:
n
c j x j max
j 1
n
aij xj ai , i 1, m
j 1
x j 0, j 1, n.
В этой задаче свободные члены ai могут иметь любой знак, однако самое существенное – это неположительность всех коэффи-
циентов целевой функции ( cj 0, j=1,2,...,n ).
Придадим этой задаче каноническую форму, используя дополнительные переменные:
n
c j x j max
j 1
n
aij x j xn i ai , i 1, m
j 1
x j 0, j 1, n m .
Очевидно, что вектор
x (x1, x2 ,..., xn m ) ( 0,0,...,0,a1,a2,...,am )
удовлетворяют всем ограничениям-уравнениям этой задачи. Векторы при дополнительных переменных An+1,An+2 ,...,An+m
линейно независимы и составляют полный единичный базис системы ограничений-уравнений ( B=E ).
Учитывая, что B=B-1=E , найдем оценки всех небазисных векторов:
|
j=cбазB-1Aj - cj , ( j=1,2,...,n ). |
|
Но cбаз=( 0,0,...,0 ), т.е., j = - cj , ( j=1,2,...,n ), |
а по условию |
|
задачи все cj 0, |
j=1,2,...,n . Следовательно, все j |
0, т.е. x – |
псевдоплан, которому соответствует допустимое решение двойст-
венной задачи: y=cбазB-1=( 0,0,...,0 ). 111

Требование cj 0 – это достаточно серьезное ограничение, но тем не менее класс подобных моделей весьма широк.
Пример 1.21
Дана задача ЛП: |
|
|
|
|
|
|
|
|
|
||
3x1 |
+ |
6x2 |
min, |
|
-3x1 |
- |
6x2 |
max |
|||
x1 |
|
|
|
1 |
|
|
-x1 |
|
|
|
-1 |
x1 |
+ |
2x2 |
|
5 |
|
|
x1 |
+ |
2x2 |
5 |
|
4x1 |
- |
3x2 |
|
10 |
|
|
4x1 |
- |
3x2 |
|
10 |
|
|
x1,2 |
|
0 |
|
|
|
|
x1,2 |
|
0 |
|
Приведем систему ограничений к каноническому виду: |
|
|||||||||
|
|
|
-3x1 |
- |
6x2 |
|
|
max |
|
|
|
|
|
|
-x1 |
|
|
+x3 |
|
= |
-1 |
|
|
|
|
|
x1 |
+ |
2x2 |
+x4 |
|
= |
5 |
|
|
|
|
|
4x1 |
- |
3x2 |
|
+x5 |
= |
10 |
|
|
xj 0, j=1 5.
Решение задачи двойственным симплекс-методом:
Баз |
Cбаз |
A0 |
-3 |
|
|
-6 |
|
|
0 |
|
0 |
|
0 |
|
|||
A1 |
|
|
A2 |
|
|
A3 |
|
A4 |
A5 |
||||||||
A3 |
0 |
-1 |
|
|
-1 |
|
0 |
|
1 |
|
0 |
|
0 |
|
|||
A4 |
|
|
1 |
|
|
1 |
|
|
0 |
|
|
-1 |
|
0 |
|
0 |
|
0 |
5 |
|
|
1 |
|
|
2 |
|
|
0 |
|
1 |
|
0 |
|
||
A5 |
0 |
10 |
|
4 |
|
-3 |
|
0 |
|
0 |
|
1 |
|
||||
Tабл.1 |
|
0 |
|
3 |
|
6 |
|
0 |
|
0 |
|
0 |
|
||||
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
-3 |
1 |
|
|
1 |
|
0 |
|
-1 |
|
0 |
|
0 |
|
||||
A4 |
0 |
4 |
|
|
0 |
|
2 |
|
1 |
|
1 |
|
0 |
|
|||
A5 |
0 |
6 |
|
|
0 |
|
-3 |
|
4 |
|
0 |
|
1 |
|
|||
Tабл.2 |
|
|
-3 |
|
0 |
|
6 |
|
3 |
|
0 |
|
0 |
|
|||
Итак, оптимальное решение канонической задачи:
Z = -3; Xопт=( 1,0,0,4,6 ).
Оптимальное решение исходной задачи:
Zисх = 3; Xопт=( 1,0 ).
Задача, двойственная к канонической, имеет следующее реше-
ние:
Zдв = - 3; Y=( 3,0,0 ).
Определение исходного псевдоплана введением дополнительного ограничения
Пусть дана каноническая задача ЛП, имеющая n+m переменных. Каким угодно способом придадим задаче следующую форму:
112

n m
c j x j max
j 1
n
aij x j xn i ai , i 1, m
j 1
x j 0, j 1, n m.
Здесь свободные члены ai (i=1,2,...,m) могут иметь любой
знак.
Очевидно, что вектор
x (x1, x2 ,..., xn m ) ( 0,0,...,0,a1,a2,...,am )
удовлетворяет всем ограничениям-уравнениям этой задачи, причем переменным xn 1, xn 2 ,..., xn m , имеющим значения a1,a2,...,am , соот-
ветвует полная система единичных (линейно-независимых) векто-
ров: An+1,An+2,...,An+m.
По сути, задаче в такой форме соответствует вполне определенная симплекс-таблица:
Баз |
Сбаз |
А0 |
с1 |
|
сk |
|
сn |
сn+1 |
|
|
сn+m |
|
|
|
|
|
А1 |
|
Аk |
|
Аn |
Аn+1 |
|
|
Аn+m |
|
|
Аn+1 |
сn+1 |
x10 |
x11 |
|
x1k |
|
x1n |
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аn+m |
сn+m |
xm0 |
xm1 |
|
xmk |
|
xmn |
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
1 |
|
k |
|
n |
0 |
|
|
|
0 |
|
Следует обратить внимание на тот факт, что оценки векторов могут иметь любые знаки и, главное, среди коэффициентов разложения вектора А0 могут быть отрицательные. То есть, записанное в таблице решение – это не псевдоплан и не опорное решение.
Введем в состав ограничений дополнительное ограничение, имеющее вид:
n
xj xn m 1 M , j 1
где xn m 1 – дополнительная переменная, а М – достаточно
большое положительное число. Это число подбирается таким образом, чтобы полупространство x1+x2+...+xn M полностью вклю-
113
чало в себя все допустимое множество задачи. Это множество ( D ), учитывая что все xn+i 0 , можно представить в виде:
n
aij xj ai , i 1, m
j 1
x j 0, j 1, n.
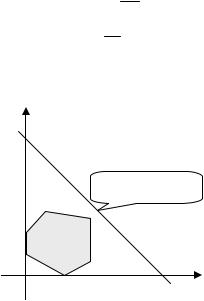
Графически, подбор значения М можно проиллюстрировать следующим образом (рис.1.14):
x2
x1+x2=M
D
x1
Рис.1.14. Иллюстрация подбора достаточно большого числа M
Введение нового ограничения приводит к следующему изменению в симплекс-таблице:
1в базис вводится единичный вектор An+m+1=( 0,0,...,0,1 )T c единицей в m+1-й позиции;
2все базисные векторы An+1,An+2,...,An+m дополняются нулевой m+1-й координатой;
3все свободные векторы A1,A2,...,An дополняются единичной
m+1-й координатой ( xm+1,j=1 ).
Ввиду того, что cn+m+1=0 , оценки векторов не изменяются. Новой задаче соответствует следующая симплекс-таблица:
114

Баз |
Сбаз |
А0 |
с1 |
|
|
сk |
|
|
сn |
сn+1 |
|
|
|
сn+m |
|
0 |
|
|
|
|
А1 |
|
|
Аk |
|
|
Аn |
Аn+1 |
|
|
|
Аn+m |
|
Аn+m+1 |
|
Аn+1 |
сn+1 |
x10 |
x11 |
|
|
x1k |
|
|
x1n |
1 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аn+m |
сn+m |
xm0 |
xm1 |
|
|
xmk |
|
|
xmn |
0 |
|
|
|
1 |
|
0 |
|
Аn+m+1 |
0 |
М |
1 |
|
|
1 |
|
|
1 |
0 |
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
0 |
1 |
|
|
k |
|
|
n |
0 |
|
|
|
0 |
|
0 |
|
Выведем из базиса вектор An+m+1 и заменим его некоторым небазисным вектором Ak ( k [1,2,...,n] ). Подсчитаем новые оценки свободных векторов Aj ( j [1,2,...,n] ):
j j xm 1, j k j k .
xm 1,k
Очевидно, что для того чтобы все новые оценки j стали не-
отрицательными, в базис нужно вводить вектор с наименьшей из отрицательных оценок.
При выполнении этого условия новому базису будет соответствовать псевдоплан: ( x10 , x20 ,..., xm 1,0 ).
Пересчитав по основным формулам все элементы, имеем исходную симплекс-таблицу для работы по двойственному симплексметоду.
Столбец An+m+1 в последующих вычислениях игнорировать. Число М находится непосредственно из условий задачи или
решением вспомогательной задачи:
n
xj max
j 1
n
aij xj ai , i 1, m
j 1
x j 0, j 1, n.
Если исходная задача имеет хотя бы одно ограничение – нестрогое неравенство вида
ai1x1+ai2x2+...+ainxn ai , где aij >0; ai >0,
то число M можно определить более простым способом.
115
Приведем эти неравенства к виду:
|
x1 |
|
x2 |
... |
|
xn |
1. |
|||
|
a |
a |
|
a |
||||||
|
i |
|
i |
|
|
|
|
i |
|
|
|
ai1 |
|
ai2 |
|
|
ain |
|
|
||
Очевидно, что если взять |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a |
i |
|
, |
|||
|
|
M max |
|
|
|
|||||
|
|
|
|
|
||||||
|
|
|
|
j 1,n aij |
|
|||||
|
|
|
|
|
|
|
|
|
||
то ограничение
x1+x2+...+xn М
не сократит область допустимых решений.
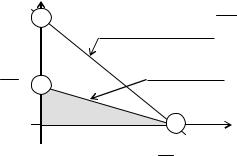
Этот подход в двумерном случае можно проиллюстрировать следующим образом.
Допустим в системе ограничений имеется ограничение вида:
ai1x1+ai2x2 ai , где aij >0; ai >0 (рис.1.15). x2
|
ai |
|
x1 x 2 |
max |
|
|
||
|
ai1 |
|
,aai
i2
ai ai1x1+ai2x2 = ai
ai2
x1
ai
ai1
Рис.1.15. Выбор числа M для двумерного случая
Таким образом, нужно взять минимальный положительный элемент ( пусть это будет ais ) и принять M=ai /ais .
116

Пример 1.22
Найти исходный псевдоплан следующей задачи ЛП:
8x1 |
+5x2 |
-2x3 |
-4x4 |
+5x5 |
+x6 |
+3x7 |
|
max |
x1 |
-2x2 |
+2x3 |
+4x4 |
-4x5 |
+x6 |
|
= |
-2 |
x1 |
+2x2 |
+3x3 |
+4x4 |
+5x5 |
|
+x7 |
= |
1 |
xj 0, j=1 7.
В этой задаче, учитывая что базисная переменная x7 0 , второе ограничение-уравнение можно представить в виде:
x1 |
+2x2 |
+3x3 |
+4x4 |
+5x5 |
|
1. |
Все параметры этого ограничения положительные. Находим ми- |
||||||
нимальный |
коэффициент |
min{ a2j }=a21=1, |
откуда определяем |
|||
M= max{ a2 /a2j }= 1. |
|
|
|
|
|
|
Дополнительное ограничение имеет вид |
|
|
||||
x1 |
+x2 |
+x3 |
+x4 |
+x5 |
|
1. |
Это ограничение вводим в состав ограничений исходной задачи и придаем ему форму равенства (путем введения дополнительной пере-
менной x8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8x1 |
+5x2 |
-2x3 |
|
-4x4 |
+5x5 |
+x6 |
|
+3x7 |
|
max |
|||||||
x1 |
-2x2 |
+x3 |
|
+x4 |
-4x5 |
+x6 |
|
|
|
|
= -2 |
||||||
x1 |
+2x2 |
+3x3 |
|
+4x4 |
+5x5 |
|
|
|
+x7 |
|
= |
1 |
|||||
x1 |
+x2 |
+x3 |
|
+x4 |
+x5 |
|
|
|
|
|
+x8 |
= |
1 |
||||
|
|
|
|
|
|
xj 0, j=1 8. |
|
|
|
|
|
|
|
|
|
||
|
Ниже представлена симплекс-таблица, соответствующая этой за- |
||||||||||||||||
даче. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Баз |
|
Cбаз |
|
A0 |
|
8 |
5 |
-2 |
|
-4 |
|
5 |
1 |
3 |
|
0 |
|
|
|
|
A1 |
A2 |
A3 |
|
A4 |
|
A5 |
A6 |
A7 |
|
A8 |
|||
|
A6 |
|
1 |
|
-2 |
|
1 |
-2 |
2 |
|
4 |
|
-4 |
1 |
0 |
|
0 |
|
A7 |
|
3 |
|
1 |
|
1 |
2 |
3 |
|
4 |
|
5 |
0 |
1 |
|
0 |
|
A8 |
|
0 |
|
1 |
|
1 |
1 |
1 |
|
1 |
|
1 |
0 |
0 |
|
1 |
Tабл.1 |
|
|
|
1 |
|
-4 |
-1 |
13 |
|
20 |
|
6 |
0 |
0 |
|
0 |
|
Минимальную по абсолютной величине оценку имеет вектор А1 . |
|||||||||||
Вводим этот вектор в базис, а выводим дополнительный вектор А8 . |
|||||||||||
Имеем следующую симплекс-таблицу: |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Баз |
Cбаз |
A0 |
8 |
5 |
-2 |
-4 |
5 |
1 |
3 |
0 |
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
|
|||
A6 |
1 |
-3 |
0 |
-3 |
1 |
3 |
-5 |
1 |
0 |
-1 |
|
A7 |
3 |
0 |
0 |
1 |
2 |
3 |
4 |
0 |
1 |
-1 |
|
A1 |
8 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|
Табл.2 |
|
5 |
0 |
3 |
17 |
24 |
10 |
0 |
0 |
4 |
|
Все оценки неотрицательны, а в столбце А0 имеется отрицательный элемент. Следовательно, получен псевдоплан задачи
x= ( 1,0,0,0,0,-3,0,0 ).
117
Контрольные вопросы и задачи к разделу 1.3
1.Покажите взаимодвойственность следующей пары задач:
c, x min,
A0T , y max,AX A ,
|
0 |
AT Y C. |
x 0. |
|
|
|
|
2. Рассмотрим следующую задачу линейного программирования. Пусть для функционирования атомной электростанции применяется n видов топлива. Существует m характеристик этих видов топ-
лива. Пусть aij – i-я характеристика j-го вида топлива, ai – мини-
мально допустимое требование по i-й характеристике для электростанции в целом. Пусть cj – стоимость одной тонны топлива вида
j. Необходимо определить план закупки топлива для электростанции, минимальный по затратам при условии обеспечения выполнения минимальных требований по всем характеристикам. Постройте модель линейного программирования, соответствующую описанной задаче, постройте двойственную модель и приведите её экономическую интерпретацию.
3.Сформулируйте основные положения двойственного симплексметода для задачи на минимум целевой функции.
4.Чему соответствует псевдоплан при графической интерпретации задачи линейного программирования?
5.Почему задача получения исходного псевдоплана не всегда имеет решение?
6. Постройте задачу, двойственную к заданной x1 2x2 4x3 x4 min
x1 x2 2x3 x4 10
x1 3x2 2x3 5x4 6 4x1 x2 3x3 8x4 15
x1,3,4 0
x2 не ограничена в знаке.
7. Решите задачу симплекс-методом и получите оптимальное решение задачи, двойственной к заданной
118

6x1 6x2 max
2x1 4x2 102
4x1 3x2 114 x1 18
x2 20
x1,2 0.
8. После очередной (не первой) итерации решения задачи ЛП (на максимум) двойственным симплекс-методом получена следующая симплекс-таблица. Найдите все элементы базисной матрицы оптимального решения этой задачи и обратной к ней матрицы.
|
|
Баз |
Сбаз |
А0 |
-1 |
|
-18 |
1 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
А1 |
|
А2 |
|
А3 |
|
А4 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
А1 |
-1 |
2 |
1 |
|
-2 |
-1 |
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А4 |
2 |
-5 |
0 |
|
-4 |
2 |
|
1 |
|
|||
9. Задача |
|
ЛП |
|
|
|
|
|
|
|
|
симплекс- |
|||
|
на |
максимум |
решается двойственным |
|||||||||||
методом. Найти области параметров x |
и y, в которых: |
|
|
|||||||||||
получено оптимальное решение задачи;
задача не имеет решения;
решение следует продолжить.
Баз |
Сбаз |
А0 |
-1 |
-18 |
1 |
2 |
|||||
|
|
|
|
|
|
|
|
||||
|
А1 |
|
А2 |
|
А3 |
|
А4 |
||||
|
|
|
|
|
|
|
|
||||
А1 |
-1 |
2 |
1 |
-2 |
-1 |
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
А4 |
2 |
x |
0 |
|
y |
2 |
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
119
10. Получите исходный псевдоплан и решите задачу двойственным симплекс-методом
9x1 6x2 max
3x1 4x2 125
4x1 3x2 120 x1 18
x2 23
x1,2 0
1.4. Вопросы вычислительной эффективности в симплекс-методе
1.4.1. Обоснование модифицированного симплекс-метода
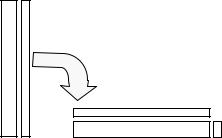
Теория двойственности предоставила мощный аппарат для решения емких с точки зрения вычислений задач (рис.1.16):

 extr
extr
extr'
Рис.1.16. Решение двойственной задачи вместо прямой для ускорения вычислений
Тем не менее, существуют иные резервы повышения эффективности.
120
