
Жолобов Ввведение в Математическое 2008
.pdfA (a , a |
2 |
,..., a |
m |
)T |
– матрица-столбец, составленная из сво- |
|
0 |
1 |
|
|
|
||
бодных членов системы ограничений;
A |
j |
(a |
|
, a |
2 j |
,..., a |
mj |
)T – матрица-столбец из коэффициентов |
||||||
|
1 j |
|
|
|
|
|
|
|
|
|||||
при переменной |
|
xj; |
)T |
– матрица-столбец из переменных задачи. |
||||||||||
X ( x , x |
2 |
,..., x |
n |
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
Тогда в матрично-векторной форме задача будет иметь вид: |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
c, x max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AX A0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
" |
|
|
"– скалярное |
произведение векторов; x 0 озна- |
|||||||||
чает, что все xj 0( j 1,2,...,n).
В векторной форме эта задача будет записана следующим образом:
|
c, x max |
|
A2 x2 ... An xn A0 |
A1 x1 |
|
|
x 0. |
|
1.2.2. Свойства задач линейного программирования
Вектор x x1, x2 ,..., xn , удовлетворяющий всем ограничени-
ям задачи, называется допустимым решением или планом задачи.
Допустимое решение, на котором целевая функция достигает своего оптимального значения, называется оптимальным решени-
ем или оптимальным планом задачи.
Множество всех допустимых решений задачи линейного программирования называется допустимым множеством.
Рассмотрим структуру допустимого множества задачи линейного программирования на примере общей задачи:
21
n |
|
|
|
|
|
c j x j max |
|||||
j 1 |
|
|
|
|
|
n |
|
|
|
|
|
aij x j ai |
(i |
|
|
) |
|
1, k |
|||||
j 1 |
|
|
|
|
|
n |
|
|
|
|
|
aij x j ai |
(i |
|
) |
||
k 1, m |
|||||
j 1
x j 0, (j 1, n1 , n1 n)
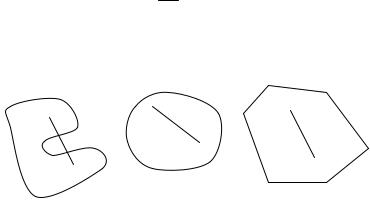
Множество называется выпуклым, если оно вместе с любыми
своими двумя точками x1 и x2 содержит все точки отрезка, соединяющего эти точки (рис.1.1).
x2 |
|
x2 |
|
x2 |
|
x |
1 |
|
x1 |
|
x1 |
|
|
|
|||
|
|
|
|
|
|
Невыпуклое множество |
|
Выпуклые множества |
|||
Рис.1.1. Выпуклые и невыпуклые множества
Известно, что множество точек, удовлетворяющих ограничению – нестрогому неравенству, представляет собой полупространство n-мерного евклидова пространства. Множество же точек, удовлетворяющих ограничению-уравнению – это гиперплоскость n-мерного евклидова пространства.
Следовательно, допустимое множество произвольной задачи линейного программирования – это пересечение полупространств и гиперплоскостей.
Ввиду того, что как гиперплоскости, так и полупространства являются выпуклыми множествами, их пересечение, если оно не пусто, также является выпуклым множеством. Отсюда вытекает следующее свойство задачи линейного программирования.
Допустимое множество произвольной задачи линейного программирования – это выпуклое множество. В дальнейшем будем обозначать это множество символом D.
22
В задачах линейного программирования градиент целевой функции не зависит от того, в какой точке он вычисляется:
grad (c1 x1 c2 x2 ...cn xn ) (c1 ,c2 ,...,cn ) .
Следовательно, локальные экстремумы отсутствуют, и, если коэффициенты целевой функции одновременно не равняются нулю, целевая функция может достичь своего экстремального значения только на границе допустимого множества D. Отсюда следует второе свойство задачи ЛП.
Задача линейного программирования на максимум(минимум) целевой функции имеет решение только в том случае, если ее целевая функция на множестве D ограничена сверху (снизу).
Границей множества D называется подмножество точек, каждая из которых в любой своей -окрестности содержит как точки этого множества, так и точки, не принадлежащие ему.
В задаче линейного программирования граница в явном виде не задана, поэтому основной проблемой является определение этой границы – ведь согласно свойству 2 экстремум целевой функции, если он существует, достигается на границе допустимого множества D.
Особая роль в методах решения задач линейного программирования отводится вершинам множества D, которые называются также угловыми точками.
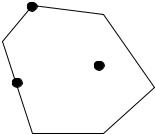
Точка x D называется вершиной множества D, если она не может быть представлена в виде выпуклой линейной комбинации с отличными от нуля коэффициентами никаких двух других точек этого множества (рис.1.2).
|
x1 |
|
|
x1 – вершина |
|
|
x2 |
– не вершина |
x2 |
x3 |
|
x3 |
– не вершина |
|
Рис.1.2. Вершины множества
23
Роль вершин раскрывается в следующем свойстве задачи линейного программирования.
Если задача имеет решение и ее допустимое множество D имеет хотя бы одну вершину, то и оптимального значения целевая функция достигает в вершине множества D.
1.2.3. Геометрическая интерпретация задач линейного программирования
Рассмотрим задачу линейного программирования в стандартной форме:
c1x1 c2 x2 max,
ai1x1 ai2 x2 ai , i 1,2,...,m, x1, x2 0.
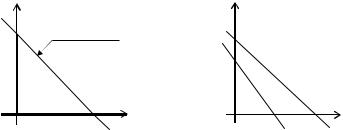
Что представляет собой ограничение ai1 x1 ai 2 x2 ai ? Это ограничение определяет на плоскости одну из полуплоскостей, на
которые прямая ai1 x1 ai 2 x2 |
ai |
разбивает плоскость (рис.1.3). |
x2 |
|
x2 |
ai1x1 ai2 x2 ai
x1 |
x1 |
|
|
Рис.1.3. Допустимое множество |
Рис.1.4. Пустое допустимое множество |
|
|
Очевидно, что допустимое множество задачи – это пересечение m полуплоскостей положительного квадранта, каждая из которых является множеством точек, удовлетворяющих соответствующему ограничению – нестрогому неравенству.
24
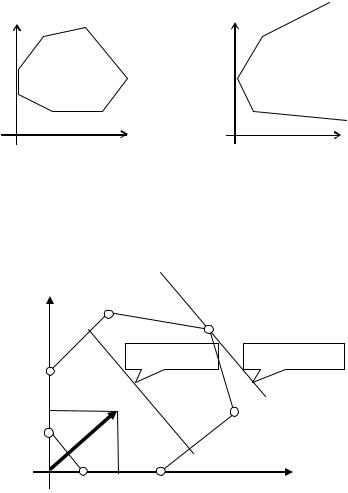
Ясно, что такое пересечение может соответствовать "пустому" множеству (рис.1.4), ограниченному множеству (рис.1.5) и, наконец, неограниченному множеству (рис.1.6).
x2 |
x2 |
x1 |
x1 |
Рис.1.5. Ограниченное |
Рис.1.6. Неограниченное |
допустимое множество |
допустимое множество |
Предположим, что множество D – ограниченное множество и представляет собой выпуклый многогранник с вершинами S1,
S2,...,S7 (рис.1.7).
x1 |
S6 |
|
|
S5 |
|
|
|
|
S7 |
c1x1+c2x2=h |
c1x1+c2x2=h* |
|
|
|
c2 |
C |
S4 |
S1 |
|
|
|
|
S2 |
c1 |
S3 |
x2 |
Рис.1.7. Интерпретация задачи линейного программирования
25
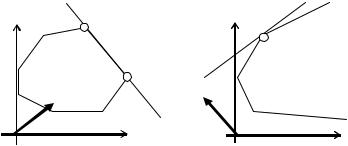
Целевая функция c1x1+c2x2 принимает одно и то же значение h на всех точках прямой c1x1+c2x2 = h , которая называется
линией уровня.
Приняв h в качестве параметра, начнем увеличивать этот параметр. Очевидно, что увеличение h приведет к перемещению линии уровня в направлении нормали – вектора с=(c1,c2).
При некотором значении h = h* линия уровня станет опорной к многоугольнику D. Очевидно, что h* – максимальное значение целевой функции, которому соответствует оптимальное решение задачи линейного программирования (x1 , x2 ) – вершина S5.
В данном случае имеет место единственное решение.
Из геометрических соображений ясно, что задача линейного программирования может иметь бесконечное множество оптимальных решений (рис.1.8). Кроме того, задача может иметь оптимальное решение и при неограниченном допустимом множестве
(рис.1.9).
x2 |
x2 |
C C
x1 |
x1 |
Рис.1.8. Пример задачи с бесконечным |
Рис.1.9. Пример оптимального |
числом оптимальных решений |
решения задачи на бесконечном |
|
множестве |
Во всех же случаях, когда задача линейного программирования имеет решение, по крайней мере одно из оптимальных решений соответствует вершине ее допустимого множества.
Это обстоятельство позволяет не рассматривать все точки границы допустимого множества: достаточно знать лишь координаты его вершин. Для каждой вершины можно вычислить соответ-
26
ствующее значение целевой функции, после чего выбрать одну вершину, координаты которой доставляют целевой функции максимальное значение.
Однако даже для задач небольшой размерности такой путь не является приемлемым, так как количество вершин может оказаться весьма большим.
Допустим, известны координаты одной какой-либо вершины. В этом случае, очевидно, не имеет смысла рассматривать вершины,
вкоторых целевая функция принимает худшее значение. То есть, необходимо найти путь перехода к вершине с лучшим значением целевой функции. Такой переход можно осуществить по ребру допустимого множества – к смежной вершине.
Естественно, такой подход существенно сокращает количество просматриваемых вершин допустимого множества. Однако, его следует дополнить: при переходе к очередной вершине необходимо уметь устанавливать признак того, что лучших вершин нет (текущая вершина соответствует максимальному значению целевой функции), а также признак неограниченности сверху целевой функции (признак того, что ребро, по которому следует переходить
всторону увеличения целевой функции, является неограниченным ребром).
Вэтом, собственно, и заключается суть симплекс-метода, самого распространенного в настоящее время метода решения задач линейного программирования.
27
Пример 1.6 |
|
|
|
|
|
|
|
|
|
|
|
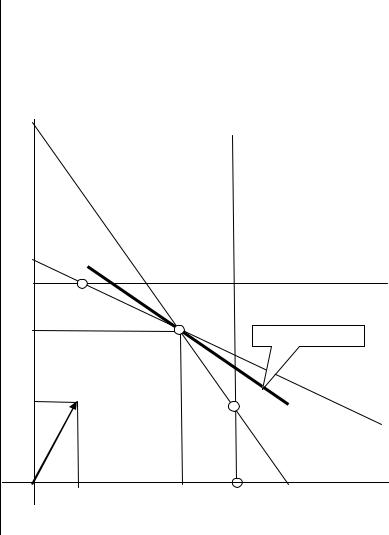
Решить графически задачу линейного программирования: |
|
|
|
||||||||
|
|
|
2x1 + 3x2 → max |
|
|
|
|
|
(а) |
||
|
|
|
x2 ≤ 80 |
|
|
|
|
|
|
|
|
|
|
|
x1 + 2x2 ≤ 180 |
|
|
|
|
|
|
(б) |
|
|
|
|
3x1 + 2x2 ≤ 300 |
|
|
|
|
|
(в) |
||
|
|
|
x1 |
≤ 80 |
|
|
|
|
|
|
(г) |
|
|
|
x1, x2 ≥ 0 |
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
|
|
140 |
|
|
|
|
|
|
|
|
|
|
|
130 |
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
|
110 |
|
|
|
|
|
|
(г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
(в) |
|
|
|
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|
|
(а) |
|
80 |
|
|
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
2x1 + 3x2 = 300 |
|
||
50 |
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
(б) |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
xopt=(60, 60), zopt=2*60+3*60=300 |
|
|
|
|
|
|
|
||||
28

1.2.4. Основные понятия симплекс-метода
Пусть дана каноническая задача линейного программирования в векторной форме:
<c,x>→max |
(1.5) |
A1x1 + A2x2+...+ Anxn=A0 |
(1.6) |
x ≥ 0 |
(1.7) |
Пусть ранг матрицы A=(A1,A2,...,An) равен m – числу ограни-
чений-уравнений. Будем считать, что m < n. Заметим, что в случае m = n система уравнений (1.6), если она совместна, является крамеровской и имеет единственное решение.
Задачу (1.5-1.7) будем трактовать следующим образом. Из всех возможных представлений вектора A0 в виде линейной комбинации векторов A1, A2, …, An с неотрицательными коэффициентами выбрать такое, коэффициенты которого доставляют целевой функции (1.5) максимальное значение.
Учитывая роль вершин допустимого множества D, которое определяется ограничениями (1.6), (1.7), необходимо уметь определять, в каком случае допустимому решению x = (x1, x2 ,..., xn ) соот-
ветствует вершина допустимого множества D.
Известно, что векторы A1, A2, …, An составляют линейнонезависимую систему, если не существует такого набора чисел α1, α2, …, αn одновременно не равных нулю, что:
|
α1A1 + α2 A2 +...+αn An = 0. |
|
|||||||||
Допустимое решение |
|
= ( |
|
, |
|
,..., |
|
) |
называется опорным ре- |
||
x |
x1 |
x2 |
xn |
||||||||
шением (или |
опорным планом), |
если |
векторы Aj |
||||||||
(j=1,2,...n), соответствующие положительным координатам вектора x в разложении вектора A0 (2), составляют линейнонезависимую систему. Если нулевой вектор – допустимое решение, то его также будем считать опорным решением.
Пример 1.7
Допустим, система ограничений задачи линейного программирования имеет вид:
2x1+ x2+ 3x3 + |
4x5 = 2, |
|
x1 |
-2x3 + x4 +2x5 = 1 |
|
|
xj ≥ 0, ( j=1,2,...,5 ). |
|
Здесь ранг системы равен двум |
– количеству ограничений- |
|
|
29 |
|
уравнений.
Рассмотрим следующие допустимые решения:
x(1) = (0, 2, 0, 1, 0) – это решение опорное, так как векторы A2 и A4 составляют линейно-независимую систему;
x(2) = (1, 0, 0, 0, 0) опорное;
x(3) = (1/2, 0, 0, 0, 1/4) не опорное, так как векторы A1 и A5 - ли- нейно-зависимые векторы;
x(4) = (1/2, 1, 0, 1/2, 0) – это решение не опорное, так как имеет три положительные координаты, а ранг равен двум (векторы A1 , A2 , A4
линейно-зависимы).
Опорное решение называется невырожденным, если оно содержит точно m положительных координат. Если количество положительных координат меньше, чем m, то решение называется вырожденным.
|
|
|
|
В примере 1.7 решение |
|
(1) – невырожденное опорное реше- |
||||||
|
|
|
x |
|||||||||
ние; |
|
|
(2) – вырожденное. |
|
|
|||||||
|
x |
|
|
|||||||||
|
|
|
|
Базисом опорного решения называется такой упорядоченный |
||||||||
набор |
m |
линейно-независимых векторов: Ai |
, Ai ,..., Ai ; |
|||||||||
|
|
|
|
|
|
1 |
2 |
m |
||||
|
k |
|
{ |
} |
|
|
), который включает в себя все векторы, |
со- |
||||
(i |
|
|
|
1, 2,..., n , |
k = |
1, m |
||||||
ответствующие положительным координатам этого опорного решения.
Очевидно, что базис однозначно определяется по невырожденному опорному решению. Если же решение является вырож-
денным, то возникает неопределенность. Так, для решения X2 = (1,0,0,0,0) не ясно: в совокупности с каким вектором вектор A1 со-
ставляет базис этого решения.
Если некоторая подсистема m векторов является базисом опорного решения, переменные, соответствующие векторам этой подсистемы в разложении вектора A0 (2), называются базисными;
остальные переменные – свободными.
Связь вершин допустимого множества D задачи линейного программирования с опорными решениями устанавливается следующей теоремой.
30
