Жолобов Ввведение в Математическое 2008

2.1. Некоторые виды задач дискретного программирования

2.1.1. Линейное целочисленное программирование

Главным образом, в линейном целочисленном программировании исследуется модель следующего вида:

При n=n1 имеет место задача линейного целочисленного программирования; при n>n1 задача линейного частично- целочисленного программирования.

Условие целочисленности (2.4) может быть заменено требо-

ванием дискретности:

В этом случае имеет место задача линейного программирования с дискретными переменными.

Частным случаем задачи линейного целочисленного программирования (ЛЦП) является задача линейного целочисленного программирования с булевыми переменными ЛЦП(б):

n

cj xj max (min)

Это – очень важный класс задач. Достаточно сказать, что если заранее установлены пределы возможных значений переменных, любая задача дискретного или целочисленного программирования может быть сведена к задаче ЛЦП(б).

211

2.1.2. Сведение к задачам булева программирования задач линейного программирования с дискретными переменными

Пусть имеется задача линейного программирования с дискретными переменными:

x j 0 ( j 1, n) .

Введем булевы переменные (по одной переменной на каждое дискретное значение):

2.1.3. Сведение к задачам булева программирования некоторых нелинейных задач с дискретными переменными

Отдельные нелинейные задачи с дискретной областью определения переменных могут быть сведены к виду ЛЦП(б)-задачи.

x j 0 ( j 1, n) .

Пусть далее в целевой функции или в ограничениях фигурирует нелинейная функция (xj ) (рис. 2.1). Эта функция, в част-

ности, может быть задана таблично.

( x j )

k j

(xj ) = (dlj ) ylj .

l 1

Теперь, для того чтобы (xj ) принимало одно и только одно

значение из множества (2.6), введем ограничение:

k j ylj 1. l 1

Произведем замену переменной x j :

k j

xj dlj ylj . l 1

Пример 2.1

Дана нелинейная задача:

n

(x1 ) cj xj max

j 2

x j {1, 2, 3, 4} ( j 1, n ).

Свести задачу к задаче линейного программирования с булевыми переменными.

l 1

Потребуем, чтобы только одна булева переменная принимала единич-

4

ное значение: yl 1 .

l 1

4

Представляем (xj ) в виде: (xj ) = (l) yl .

l 1

Окончательно:

214

l 1

x j {1, 2, 3, 4} ( j 2, n )

yl {0,1} l=1, 4.

Если оптимальное решение задачи представлено вектором:

x* x2* , x3* ,...xn* , y1* , y2* , y3* , y4* .

По этому решению определяется оптимальное значение переменной x1 исходной задачи:

4

x1 lyl* .

l 1

2.1.4.Задачи комбинаторного типа

Взадачах комбинаторного типа поиск экстремума ЦФ осуществляется на некотором множестве комбинаций элементов заданного множества. В качестве таких комбинаций могут выступать, например, перестановки, сочетания, последовательности элементов.

Как правило, множество таких комбинаций, в соответствии с содержательной постановкой задач, конечно.

Приведем самую общую постановку экстремальной задачи комбинаторного типа.

Пусть задано конечное множество G некоторых комбинаций

xi (i=1,2,…,N).

На множестве G определена некоторая функция f(xi). Эта функция может быть задана аналитически, алгоритмически и т.д.

Главное – это есть способ вычисления f(xi) для любой комбинации

xi G. Необходимо найти комбинацию, xk G, на которой ЦФ достигает минимума (или максимума):

f(xk ) max{ f (xi ) | xi G}.

Кэкстремальным задачам комбинаторного типа относятся задачи ЛЦП с ограниченным допустимым множеством.

215

Что характерно для этих задач? Характерно то, что, несмотря на конечность множества допустимых комбинаций G , мощность этого множества для реальных задач столь высокая, что прямой перебор для поиска оптимальной комбинации становится нереализуемым.

Например, в задаче о назначениях ||G||=n!; в задаче о комми-

вояжере ||G||=(n-1)!.

Ряд задач комбинаторного типа в принципе можно свести к ЛЦП(б)-задачам. Однако задачи комбинаторного типа, представленные моделями ЛЦП или ЛЦП(б)-задач, имеют очень большую размерность, что затрудняет из решение.

2.1.5. Примеры прикладных задач дискретного программирования

Задача о ранце

В этой задаче речь идет о собравшемся в поход путешественнике, который должен упаковать в ранец (рюкзак) различные полезные предметы n наименований, причем могут потребоваться несколько одинаковых предметов одного и того же наименования.

Имеется m ограничений такого типа, как вес, объем, линейные размеры и т.д.

Пусть aij – i-я характеристика предмета j-го наименования ( i 1, m ; j 1,n ); bi – ограничение по i-й характеристике предмета

(по весу, объему, и т.д.), i 1, m .

Обозначим через xj количество предметов предмета j-го наименования ( j 1,n ), запланированное к загрузке в ранец.

Предполагается, что известна «полезность» cj одного предмета j-го наименования ( j 1,n ).

Тогда модель соответствующей задачи приобретает следующий вид:

216

Это уже не задача ЛП, так как требование целочисленности не выражается линейными ограничениями16.

Задача о назначениях

Имеется n различных самолетов, которые требуется распределить между n авиалиниями.

Известно, что на j-той авиалинии i-й самолет будет приносить доход cij единиц.

Требуется так распределить самолеты, чтобы максимизировать суммарный доход. При этом, каждый самолет должен быть закреплен за соответствующей авиалинией, и на каждую авиалинию должен быть назначен самолет.

Введем булевы переменные xij ( i, j 1,n ) такие, что:

xij =1, если i-й самолет направляется на на j-ю авиалинию; xij =0, если i-й самолет не направляется на на j-ю авиалинию. Тогда модель этой задачи приобретает следующий вид:

n

xij 1, i 1, n j 1

(каждый самолет назначается только на одну линию),

n

xij 1, j 1,n i 1

(на каждую линию назначается только один самолет) xij 0,1 ; i, j 1,n .

16 Первоначально эта задача была поставлена, как задача об оптимальной загрузке бомбардировщика бомбовым грузом.

217

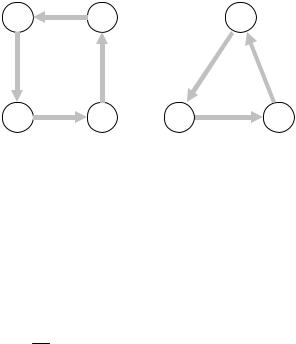
маршрут, представленный на рис.2.2, удовлетворяет всем ограничениям, но лишен смысла.

По условиям задачи маршрут должен представлять собой единственный цикл, обязательно проходящий через город «0» – исходный город.

Более точно, условия задачи должны быть дополнены такими условиями, которые запрещают любой цикл, не проходящий через город «0».

Дополним ограничения (2.8) и (2.9) ограничениями, которые на первый взгляд могут показаться несколько «искусственными»:

Здесь ui – переменные, которые могут принимать произволь-

ные значения ( i 1, n ).

Покажем, что эти дополнительные ограничения запрещают любой цикл, не проходящий через город «0».

Действительно, рассмотрим некоторое решение, удовлетворяющее ограничениям (2.8)-(2.11):

({ xij },{ ui }).

Поставим в соответствие этому решению маршрут такой, что дуга (i,j) принадлежит этому маршруту тогда и только тогда, когда

xij =1.

Вполне очевидно, что маршрут содержит цикл, так как в каждый город входит одна дуга и одна дуга выходит.

Предположим (от противного), что маршрут включает цикл, не содержащий города «0», состоящий из k дуг.

219

Очевидно, что каждой дуге этого цикла соответствует опре-

“0” не входит в маршрут).

Просуммируем неравенства, соответствующие дугам частного цикла. При этом все переменные ui сократятся, так как каждая из

них войдет в сумму дважды с противоположными знаками. Будет получено противоречивое неравенство:

nk (n 1)k ,

что доказывает неправомерность предположения о существовании такого цикла.

Таким образом, любое решение задачи (2.7)-(2.11) соответствует циклу, проходящему через город «0».

Покажем теперь, что любому циклу, проходящему через город «0», можно поставить в соответствие решение задачи (2.7)- (2.11).

Возьмем произвольный цикл:

l0 l1 l2 ln l0 ,

где l0 =0, а все lr различны ( lr 1,2,...,n , r 1,2,...,n ), т.е. r –это порядковый номер города lr в маршруте, представленном циклом.

Рассмотрим следующий план задачи: X=({ xij },{ ui }). В этом плане числа xij возьмем в соответствии с их интерпретацией в мо-

сто переезд из города i в город j) . В противном случае xij =0.

В качестве ui примем порядковый номер города lui в маршру-

те ( i 0, ui 1,2,...,n ).

Определенный таким образом план удовлетворяет всем ограничениям задачи (2.7)-(2.11).

Действительно:

1. Возьмем xij =0. Тогда соответствующее ограничение системы (2.11) будет иметь вид:

220