Жолобов Ввведение в Математическое 2008

Теперь по каждой незаполненной клетке посчитаем соответствующую косвенную стоимость Eij cij (ui vj ) :

E13=4-(2+0)=2, E22=3-(-1+2)=2, E24=5-(-1+1)=5

E31=3-(2+3)= -2, E32=2-(2+2)=-2, E34=4-(2+1)=1.

Наличие отрицательных косвенных стоимостей говорит о неоптимальности записанного в таблицу решения. Это решение можно улучшить, введя в состав базисных переменных переменную x31 или x32. ВведемДляx32этого. построим цикл пересчета.

Для определения величины находим среди отрицательных вершин такую, которой соответствует минимальное значение переменной в опорном решении. Это x33=20. Следовательно, принимаем

=20 и выполняем сдвиг по циклу пересчета. После этого сдвига переменная x33 принимает нулевое значение. Эту переменную выведем из состава базисных переменных (введем же переменную x32 ).

В табл. 3 записано новое опорное решение.

По заполненным клеткам составим систему уравнений для нахо-

251

Мы решали методом Фогеля следующую задачу (Пример 2.6):

И показали, что оно не оптимальное, так как E22= -2 < 0. Продолжим решение. Построим цикл пересчета.

Определяем = 10 и производим сдвиг по циклу пересчета. Пе-

252

По заполненным клеткам составим и решим систему уравнений:

Нет ни одной отрицательной косвенной стоимости, значит записанное в таблице решение – оптимальное.

На этом решении ЦФ принимает значение: Zопт=315 – меньшее (т.е. лучшее), чем решение, полученное ранее приближенными метода-

ми (там Zопт=335).

2.2.11. Выводы по методу потенциалов

Метод потенциалов дает нам эффективное средство подсчета косвенных стоимостей незанятых клеток таблицы – свободных переменных. Как уже отмечалось, косвенная стоимость

Eij cij (ui vj ) – это коэффициент, с которым свободная пере-

менная xij входит в ЦФ, если все базисные переменные выразить через свободные. В ЛП – это оценка соответствующего свободного вектора (правда, взятая с обратным знаком).

253

Для вычисления оценок в симплекс-методе необходимо знать коэффициенты разложения соответствующих векторов или, как в МСМ, обратную базисную матрицу текущего опорного решения.

Таким образом, первой особенностью транспортной задачи является весьма экономная процедура вычисления оценок – ни о какой обратной матрице речи не идет.

После принятия решения о том, какую переменную нужно вводить в состав базисных переменных, вопрос о том, какую переменную выводить из состава базисных переменных, решается весьма своеобразно – с использованием цикла пересчета. Здесь остаются неясности, часть из которых необходимо снять. Прежде всего, нужно строго определить понятие цикла пересчета.

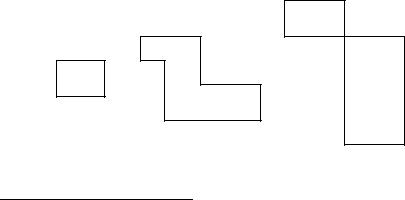
Циклом в матрице назовем ломаную, вершины которой расположены в клетках, а звенья лежат вдоль строк и столбцов матрицы (рис. 2.8). При этом ломаная должна удовлетворять следующим условиям:

1.Ломаная должна быть связной в том смысле, что из одной ее вершины можно попасть в любую другую вершину по звеньям ломаной;

2.В каждой вершине ломаной встречаются ровно два звена, причем одно из них располагается по строке, а другое – по столбцу19.

Вслучае самопересечения точка пересечения не является вершиной.

Рис.2.8. Примеры циклов в матрице

19 Если назвать две вершины, являющиеся концами одного звена, «соседними», то из условия 2) вытекает, что каждая вершина цикла обладает ровно двумя соседними: одна из них располагается по строке, другая – по столбцу.

254

Циклом пересчета данной свободной клетки назовем цикл, одна из вершин которого находится в этой свободной клетке, а все остальные – в занятых.

ТЕОРЕМА 2.1

Пусть в матрице перевозок записано некоторое опорное решение. Каков бы ни был состав свободных и базисных переменных любого опорного решения транспортной задачи, в матрице перевозок не существует цикла, все вершины которого находятся в базисных клетках.

Доказательство

Запишем систему ограничений транспортной задачи в следующей форме:

Пусть x (x11,..., xij ,..., xmn ) – опорное решение транспортной

Пусть, от противного, существует цикл, все вершины которого находятся в заполненных клетках. При этом ' – подмножество базисных переменных, входящих в цикл пересчета.

Придадим любой переменной xij ( i, j) ' некоторое прира-

щение > 0 и произведем сдвиг по циклу пересчета. Получим новое решение системы (2.20) x (x11 ,..., xij ,..., xmn ) , причем:

Ввиду того, что x x , получено новое разложение вектора A0 по тому же базису. А этого не может быть, так как разложение

любого вектора по базису единственно. Следовательно, предположение о том, что существует цикл, все вершины которого находятся в заполненных клетках, оказалось неверным. Теорема доказана.

Следствие. Для каждой свободной клетки в транспортной таблице существует единственный цикл пересчета

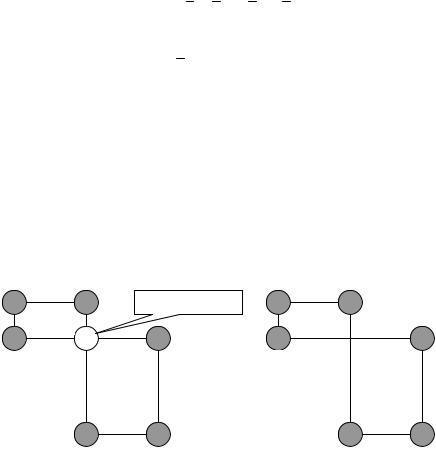
Предположим, что для некоторой свободной клетки существуют два цикла пересчета. На рис. 2.10 показано, что в этом случае при отбрасывании свободной клетки образуется цикл пересчета, все вершины которого находятся в базисных клетках, что противоречит теореме 2.1.

Свободная

Цикл 1

256

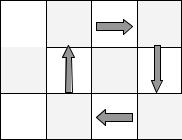
Казалось бы, приведенный пример (рис. 2.9) опровергает утверждение теоремы. Здесь цикл включает только заполненные клетки. Однако решение, записанное в таблице, хотя и допустимое, но не опорное.

Рис.2.9. Ложный пример, якобы опровергающий теорему 2.1

Цикл пересчета может не включать все базисные переменные (занятые клетки). Те из базисных переменных, которые входят в цикл в качестве положительных вершин, при переходе к новому опорному решению увеличивают свое значение на одну и ту же величину. Базисные переменные, соответствующие отрицательным вершинам, при переходе к новому опорному решению уменьшают свое значение на одну и ту же величину. Базисные переменные, не входящие в цикл пересчета, при переходе к новому опорному решению сохраняют свое прежнее значение.

2.2.12. Распределительный метод решения транспортной задачи

Пусть имеется некоторое опорное решение и xij – свободная переменная, а xkl - базисная переменная.

Построим цикл пересчета для xij .

Что касается xkl , возможны следующие ситуации:

1.xkl соответствует положительной вершине;

2.xkl соответствует отрицательной вершине;

3.xkl в цикл не входит.

257

Рассмотрим эти ситуации подробнее.

1. Если xkl соответствует положительной вершине, то при переходе к новому опорному решению xkl увеличится на ту же величину, что и xij . То есть, если выразить базисные переменные через свободные, переменная xij войдет в выражение для xkl с коэффициен-

том «+1»;

2. Если xkl соответствует отрицательной вершине, то при переходе

кновому опорному решению xkl уменьшится на ту же величину, на которую увеличится xij . То есть, если выразить базисные пере-

менные через свободные, переменная xij войдет в выражение для xkl с коэффициентом «-1»;

3. Если xkl не входит в цикл пересчета, то при переходе к новому опорному решению значение xkl не изменится. То есть, если выразить базисные переменные через свободные, переменная xij войдет

в выражение для xkl с коэффициентом «0».

Схематично эти ситуации можно представить следующим образом:

1.xkl =+1 xij +…….

2.xkl =-1 xij +…….

3.xkl =0 xij +…….

Выразим теперь ЦФ через свободные переменные.

Как подсчитать, с каким коэффициентом переменная xij вой-

дет в ЦФ?

Она войдет в соответствующее выражение непосредственно (с коэффициентом xij ) и через посредство тех и только тех базис-

ных переменных, которые входят в цикл пересчета.

Но xij входит в выражение для xkl только с одним из двух ко-

эффициентов: +1 или -1 , в зависимости от того, является вершина xkl положительной или отрицательной. А xkl входит в ЦФ

258

с коэффициентом ckl . То есть посредством xkl (входящей в цикл) переменная xij войдет в ЦФ с коэффициентом + ckl или - ckl , в

зависимости от того является вершина xkl положительной или

отрицательной.

Схематично эту ситуацию можно представить следующим образом:

Z= cij xij + ckl xkl +…

1

xkl = 1 xij +…0

1

Z= cij xij + ckl ( 1 xij +…)+…

0

1

Z= (cij 1 ckl ...) xij +…0

Как видно из этого выражения, в круглых скобках записана алгебраическая сумма всех стоимостей, которым соответствуют вершинам цикла пересчета.

Таким образом, коэффициент, с которым свободная переменная xij входит в ЦФ, равен алгебраической сумме всех стоимостей,

соответствующих вершинам цикла, включая вершину, в которой находится свободная переменная.

То есть косвенную стоимость свободной переменной xij

можно определить не по формуле Eij cij (ui vj ) , а другим пу-

тем. Нужно построить для этой переменной цикл пересчета и подсчитать алгебраическую сумму всех стоимостей, которым соответствуют вершинам цикла пересчета.

Имеется некоторое опорное решение.

259

Шаг 1. Для данного опорного решения организуем последовательный просмотр списка свободных клеток (переменных).

Шаг 2. Для очередной свободной клетки (пусть это будет xij )

строим цикл пересчета и подсчитываем алгебраическую сумму стоимостей по всем вершинам цикла ( Eij ).

Шаг 3. Если Eij < 0, выполняем шаг 4. В противном случае прове-

ряем, все ли свободные клетки просмотрены. Если да, то очередное решение оптимальное. Конец. В противном случае выполняем шаг 2.

Шаг 4. Переменную xij вводим в состав базисных переменных.

Для этого среди отрицательных вершин находим вершину с минимальным значением соответствующей базисной переменной. Пусть

это будет x . Производим сдвиг по циклу пересчета. Переменная x выводится из состава базисных переменных. Имеем новое опорное решение. Выполняем шаг 1.

Основной недостаток метода – большое количество циклов пересчета, которые приходится строить на каждой итерации. Достоинство – не нужно специально вычислять потенциалы строк и столбцов.

Если нет эффективной процедуры построения цикла пересчета, предпочтение отдается методу потенциалов.

Пример 2.11

Дана транспортная задача и известно ее опорное решение. Определить косвенные стоимости переменных x32, x34, x46.

260