Жолобов Ввведение в Математическое 2008

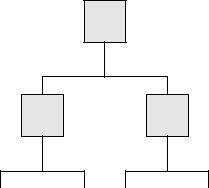
Для этого необходимо сформулировать некоторый признак пустого подмножества [8,9]. Этот признак введем следующим образом.

Преобразуем систему неравенств

n

aij xij bi , (i=1,2,...,m)

j 1

таким образом, чтобы все слагаемые в левой части этой системы стали неотрицательными. Как это сделать?

Допустим, в i-м ограничении (i=1,2,...,m) имеется отрицательный коэффициент aij < 0. Тогда вместо xj в i-е ограничение вво-

дится переменная x j =1 - xj .

Очевидно, что x j – это также булева переменная.

При этом замена переменных в других ограничениях не производится.

ai1x1+...- aijxj +...+ ainxn bi (aij 0)

ai1x1+...+ aij x j +...+ ainxn bi +aij .

В результате таких преобразований для всех отрицательных коэффициентов, все коэффициенты левой части должны стать неотрицательными. Коэффициенты правых частей также должны быть неотрицательными.

Очевидно, что если некоторое bi bi aij <0, то i-е ограни-

чение противоречиво. Ему не может удовлетворить ни один набор значений переменных. Т.е. соответствующее множество решений – пустое. Задача не имеет решений. Это и есть признак пустого множества.

Назовем операцию приведения системы ограничений к виду,

укоторого все aij > 0, операцией приведения системы ограничений

кстандартному виду [8,9].

322

В результате такого отсеивания недопустимых ветвей можно существенно сократить размерность задачи.

Но в практических ситуациях полный перебор оставшихся ветвей едва ли может привести к оптимальному решению в приемлемое время.

Здесь приведен просто прием, который используется во многих алгоритмах решения ЛЦП(б) задачи. Первым таким алгоритмом является алгоритм плотного заполнения.

2.6.2. Алгоритм плотного заполнения

Этот алгоритм, ориентированный на поиск допустимого решения ЛЦП(б) задачи, служит в качестве основы многих алгоритмов.

Система ограничений приводится к стандартной форме. Если в некотором ограничении срабатывает признак пустого

подмножества (отрицательная правая часть соответствующего неравенства), то задача не имеет решения – множество ее допустимых решений пусто.

Затем переменным задачи поочередно приписываются единичные значения. Одновременно пересчитываются правые части системы ограничений и проверяется признак пустого подмножества.

Пусть переменным x1, x2 ,..., xk 1 уже присвоены конкретные значения. Система ограничений имеет стандартную форму:

Рассмотрим общий шаг k.

Шаг k. Попытаемся приписать переменной xk единичное значение. Для этого подставим xk =1 в ограничения (2.40), учитывая вхождение этой переменной в каждое ограничение в прямом ( xk ) или в инверсном виде ( xk ).

Пересчитываем правые части ограничений:

j k 1

324

Если все bi(k ) 0 , принимаем xk =1 и выполняем шаг k0. В

противном случае – шаг k1 .

Шаг k0. Если k=n, то получено допустимое решение задачи. Конец. В противном случае выполняется шаг k+1.

Шаг k1. Попытаемся приписать переменной xk нулевое значение. Для этого подставим xk =0 ( xk ) в ограничения (2.40) и пересчитаем правые части ограничений.

левого значения.

Последовательно (в обратном порядке) просматриваем переменные x1, x2 ,..., xk 1 до тех пор, пока не обнаружим некоторую пе-

ременную xk , которой приписано единичное значение. Если такой

переменной нет, то конец – задача не имеет допустимых решений. В противном случае в исходную систему ограничений подставляем

зафиксированные ранее значения переменных x1, x2 ,..., xk 1 . Полага-

ем k=s, приводим систему ограничений к стандартному виду и выполняем шаг k1 .

Пример 2.24

Используя алгоритм плотного заполнения, найти допустимое решение следующей задачи ЛЦП(б).

4 y1 2 y2 y3 max 2 y1 y2 y3 2 y1 y2 y3 1

Произведя подстановку y1 x1 , y1 x1 , y1 x1 , приводим задачу к форме основной задачи ЛЦП(б):

325

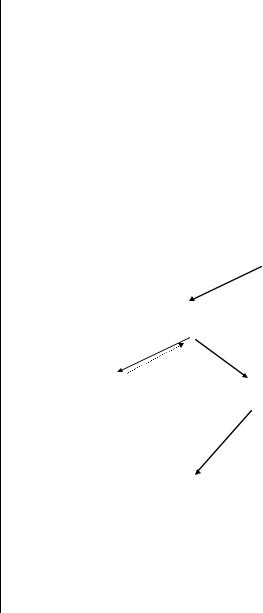
4x1 2x2 x3 1 max 2x1 x2 x3 1

x1 x2 x3 0

Приводим систему ограничений к стандартному виду:

y3 1 x3 0

326

Этот алгоритм является основой многих алгоритмов решения ЛЦП(б)-задач. Его главный недостаток – резкое увеличение времени работы, если задача не имеет допустимых решений.

2.6.3. Метод Фора и Мальгранжа

Этот метод используется для решения задачи ЛЦП(б), в которой все коэффициенты целые.

Приведем задачу к виду основной задачи (cj 0, j=1,2,...,n) и попытаемся найти любое ее допустимое решение, используя, например, алгоритм плотного заполнения.

Пусть задача имеет допустимое решение X0. F(X0) – значение ЦФ на этом решении.

К ограничениям задачи (2.43) добавим новое ограничение:

j 1

Попытаемся найти допустимое решение задачи (2.42)-(2.45). Пусть новая задача имеет допустимое решение X1. F(X1) – значение ЦФ на этом решении.

Заменим ограничение (2.45) новым ограничением:

n

cj xj F (X 1 ) 1 и снова попытаемся найти допустимое решение

j 1

задачи (2.43)-(2.45).

Этот процесс продолжается до тех пор, пока на некотором шаге k+1 не выяснится, что задача с дополнительным ограничени-

m

ем cj xj F ( X k ) 1 не имеет допустимых решений. Очевидно,

j 1

что решение предыдущей задачи Xk – оптимальное решение исходной задачи, а F(Xk) – оптимальное значение ЦФ.

327

2.6.4. Аддитивный алгоритм

Этот метод – один из наиболее популярных и мощных для решения задач ЛЦП(б) вида (2.42)-(2.44).

Рассмотрим два подмножества множества N – и v такие, что

v=N и v= .

Каждой переменной xj (j ) придадим конкретное значение x j (0 или 1). Эти переменные будем называть фиксированными.

Переменные xj (j v) оставим в прежнем виде и назовем их

свободными.

Формально определим вектор y=(y1, y2,…, yn), состоящий из следующих компонент:

Будем называть этот вектор частичным решением.

Каждому частичному решению поставим в соответствие вершину дерева ветвлений или, что то же самое, определенное подмножество решений. При этом путь от корня к этой вершине определяется значениями фиксированных переменных.

Пример 2.25

y=(1,0,x3,1,x5,x6,0) . Здесь ={1,2,4,7}, v={3,5,6}.

Для этого частичного решения дерево ветвлений выглядит следующим образом:

x1=1

x2=0

x4=1

x7=0

Подмножество из 23=8 элементов

328

Если = , то имеет место частный случай частичного решения – все переменные свободные (v N).

Любому частичному решению соответствует вполне определенная задача ЛЦП(б), которая получается из исходной задачи в результате подстановки в нее фиксированных значений переменных данного частичного решения и приведения полученной задачи к стандартной форме.

Очевидно, что если некоторое bi 0 , то соответствующее ог-

раничение противоречиво.

Следовательно, данному частичному решению соответствует недопустимая задача: все ветви, выходящие из вершины можно отбросить (как это делается в алгоритме плотного заполнения).

В противном случае (все bi 0, i 1,m ) можно предпринять

попытку расширить частичное решение. Рассмотрим некоторое ограничение задачи:

Допустим, в этом ограничении существует коэффициент

Это говорит о том, что переменная xj не может принять значение "1", если она входит в данное ограничение в прямом виде (в виде xj ). Если же переменная xj входит в ограничение в инверсном виде – в виде x'j (x'j =1 - xj), то xj не может принять значение "0".

329

Таким образом, наличие условия (2.46) позволяет приписать переменной xj только определенное значение.

Придадим этой переменной соответствующее значение. Фактически имеем новое частичное решение: один элемент j из под-

множества v перешел в подмножество .

Для полученного нового частичного решения построим задачу в стандартной форме и проведем аналогичный анализ: сначала

на допустимость ( bi 0 ), затем – на предмет существования коэффициента aij bi . Если признака недопустимости задачи нет

ствующее значение и повторим процедуру для нового частичного решения и т.д.

В результате рано или поздно возникнет одна из трех ситуа-

ций:

1.На некотором шаге установлена недопустимость задачи.

2.Нет признака пустого подмножества, но условие (2.46) не выполняется – получено новое частичное решение.

3. Все элементы из подмножества v перешли в подмножество (получено полное решение задачи).

Совокупность соответствующих операций до возникновения одной из перечисленных ситуаций назовем расширением частич-

ного решения.

Рассмотрим подробнее эти ситуации.

1.На некотором шаге установлена недопустимость задачи.

Вэтом случае исходное частичное решение недопустимо

(рис. 2.30).

2.Нет признака пустого подмножества, но условие (2.46) не выполняется. Получено новое частичное решение, которое нельзя расширить. В этом случае принудительно производится ветвление. Из одного частичного решения формируются два новых частичных решения: любой свободной переменной сначала приписывается значение "0", а затем "1".

330