
Жолобов Ввведение в Математическое 2008
.pdf
ство единицы продукции j-го вида в денежном выражении. Правая же часть – конечная стоимость этой единицы. Таким образом, с экономической точки зрения, опять ставится нерациональное требование: суммарные затраты на производство продукции не должны быть меньше стоимости этой продукции. Подобные ограничения опять-таки проистекают из природы двойственной задачи, цель которой – определить крайнюю оценку продукции, ниже которой оптимальное производство будет происходить в убыток. Для того чтобы понять это, рассмотрим условия дополняющей нежесткости из второй теоремы двойственности. Согласно этой теореме для симметричной пары задач, выражения
xj (a1 j y1 a2 j y2 ... amj ym cj ) 0, (j 1,n )
yi (ai1x1 ai2 x2 ... ain xn ai ) 0, (i 1,m )
будут справедливы только для оптимальных решений прямой и двойственных задач. Что мы видим в первом выражении? Если (a1 j y1 a2 j y2 ... amj ym cj ) 0 , т.е. в оптимальном решении
оценка затрат факторов превышает стоимость выпускаемой про-
дукции, то |
xj 0 , т.е. такая продукция в план производства вклю- |
||||
чаться не будет. Наоборот, если |
xj 0 , т.е. |
продукция j-го вида |
|||
включена |
в |
оптимальный |
план |
производства, |
то |
(a1 j y1 a2 j y2 ... amj ym cj ) 0 , т.е. оценка затрат факторов на её
производство совпадает со стоимостью единицы j-го вида продукции, что полностью согласуется с указанной выше трактовкой производства как процесса преобразования факторов в продукцию без изменения суммарной денежной стоимости.
Рассмотрим второй блок условий дополняющей нежесткости.
Если (ai1 x1 ai 2 x2 ... ain xn ai ) 0 , т.е. по окончании производства остается неиспользованным некоторое количество i-го произ-
водственного фактора, |
то |
его оценка yi 0 . И наоборот, если |
оценка i-го фактора yi |
0 , то фактор в процессе производства рас- |
|
ходуется полностью, т.е. |
(ai1 x1 ai 2 x2 ... ain xn ai ) 0 . Эти вы- |
|
ражения означают, что денежная ценность факторов в процессе производства полностью превращается в денежную ценность про-
101

дукта, а те факторы, которые не полностью используются в процессе производства, не имеют денежной ценности.
На основании всего вышесказанного можно сформулировать окончательную интерпретацию двойственной задачи. Необходимо определить неотрицательные удельные оценки всех производственных факторов, измеряемые в тех же денежных единицах, что и доход от производимой продукции, чтобы соблюдались следующие условия:
1.Суммарная оценка всех производственных факторов, участвующих в производстве единицы продукции j-го вида, не должна быть меньше выходной стоимости этой продукции.
2.Из всех допустимых вариантов таких оценок должен быть выбран тот, для которого суммарная оценка всех имеющихся к началу производства запасов производственных факторов была бы минимальной.
1.3.5. Основные понятия двойственного симплекс-метода
Симплекс-метод, описанный в разделе 1.2, заключается в последовательном переходе от одного допустимого решения задачи линейного программирования к другому – лучшему, которое доставляет целевой функции большее значение. При этом используются правила, которые гарантируют получение оптимального решения или установление неразрешимости задачи через конечное количество шагов.
Пусть теперь дана каноническая задача линейного программирования:
<c,x> max, |
(1.74) |
AX=A0 |
(1.75) |
x 0. |
(1.76) |
Пусть, далее, x (x1 , x2 ,..., xn ) – одно из решений системы
уравнений (1.75). При этом условия (1.76) могут не выполняться. Предположим, также, что ненулевым компонентам этого ре-
шения соответствует линейно-независимые векторы, которые составляют базис системы A – квадратную матрицу
B (Ai1 , Ai2 ,..., Aim ) .
Найдем коэффициенты разложения всех небазисных векторов системы A по данному базису, используя известное выражение:
102

X j B 1 Aj ,( j 1,2,...,n; j ik ,k 1,2,...,m) .
Теперь вычислим оценки всех небазисных векторов:
|
|
c |
|
|
|
1 A |
|
с |
, ( j 1,2,...,n; j i , k 1,2,...,m). |
(1.77) |
||||||
j |
B |
j |
||||||||||||||
|
баз |
|
|
|
|
|
|
|
j |
|
|
|
k |
|
||
Предположим, что все оценки (1.77) неотрицательны. |
|
|||||||||||||||
Вектор |
|
( |
|
|
|
|
|
|
удовлетворяющий системе |
ограни- |
||||||
x |
x1 , x2 ,..., xn ) , |
|||||||||||||||
чений (1.75), ненулевым координатам которого соответствует базис матрицы, построенной из коэффициентов левой части системы ограничений (1.75), называется псевдопланом задачи (1.74)-(1.76), если оценки всех векторов неотрицательны.
При доказательстве первой теоремы двойственности рассматривался случай неотрицательности оценок свободных векторов.
В частности, было доказано, что, если
|
|
c |
|
|
1 A |
|
с |
|
0 |
или |
c |
|
|
1 A |
|
с |
, |
то |
|
c |
|
|
1 – до- |
j |
|
B |
j |
j |
|
B |
j |
y |
B |
||||||||||||||
|
баз |
|
|
|
|
|
|
баз |
|
|
|
j |
|
|
|
баз |
|
|
|
пустимое решение двойственной задачи. Однако об оптимальности этого решения говорить не приходится, так как x (x1 , x2 ,..., xn )
может не удовлетворять требованию (1.76).
В этой связи псевдоплан иногда называют почти допусти-
мым опорным решением.
Очевидно, что если псевдоплан удовлетворяет требованию неотрицательности переменных (1.76), то он является оптималь-
ным решением задачи (1.74)-(1.76), а y cбазB 1 – оптимальным
решением двойственной задачи.
Каково значение целевой функции двойственной задачи на ее
допустимом решении |
|
|
c |
|
|
1 ? |
|||||||||||
|
y |
B |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
баз |
|
|
|
|
|
|
|
|
|
AT ,c |
|
|
|
|
,( |
|
1 A )T |
||||||||
|
|
|
|
|
1 c |
|
|
|
|||||||||
Z |
дв |
B |
|
|
B |
||||||||||||
|
|
|
0 |
баз |
|
|
|
|
баз |
0 |
|
|
|||||
(ci |
,ci |
,...,ci |
),(x10 , x20 ,..., xm0 ) c, |
|
, |
||||||||||||
x |
|||||||||||||||||
|
|
|
1 |
2 |
|
|
m |
|
|
|
|
|
|
|
|
|
|
т.е. значение целевой функции двойственной задачи на решении, соответствующем псевдоплану, совпадает со значением целевой функции прямой задачи на этом псевдоплане.
Таким образом, переход от одного псевдоплана к другому соответствует переходу от одного допустимого решения двойственной задачи к другому.
103
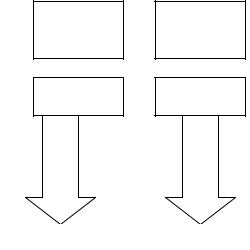
Идея двойственного симплекс-метода заключается в последовательных переходах между псевдопланами в сторону уменьшения значения целевой функции двойственной задачи.
Схема этого процесса можно приведена на рис.1.13.
<c,x> max AX=A0
x 0
ПДО-решение
<A0T,y> min ATY C
Доп. решение дв. задачи
~ 1 |
1 |
1 |
~ 1 |
x |
Zпр Zдв |
y |
|
~ 2 |
2 |
2 |
~ 2 |
x |
Zпр |
Zдв |
y |
Уменьшение значения целевой функции Рис.1.13. Общая схема двойственного симплекс-метода
Этот процесс продолжается до тех пор, пока координаты очередного псевдоплана станут неотрицательными или сработает признак неразрешимости задачи (будет установлен факт неограниченности снизу целевой функции двойственной задачи). В последнем случае, согласно утверждению первой теоремы двойственности, будет установлен факт отсутствия допустимых решений исходной задачи.
1.3.6. Обоснование двойственного симплекс-метода
Пусть базис некоторого псевдоплана составляют векторы
Ai1 , Ai2 ,..., Air 1 , , Air , Air 1 ,..., Aim . (1.78)
Заменим в этом базисе вектор Air небазисным вектором As . Согласно лемме 1.1, полученная система векторов
Ai |
, Ai |
,..., Ai |
, , As , Ai |
,..., Ai |
(1.79) |
1 |
2 |
r 1 |
r 1 |
m |
|
будет базисом системы A=(A1,A2,...,An ), если xrs 0 – r-я координата в разложении вектора As по базису (1.78).
104

ТЕОРЕМА 1.9 (о переходе к новому псевдоплану).
Если номера выводимого из базиса (1.78) вектора Air и вводимого
в базис вектора |
As таковы, что |
xrs<0, и выполняются соот- |
||||||
ношения |
|
|
|
|
|
|
|
|
|
s |
|
j |
|
|
для всех xrj 0 |
j 1, 2,..., n , |
(1.80) |
|
xrj |
|
||||||
|
xrs |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
то новому базису (1.79) будет соответствовать псевдоплан.
Доказательство. Для того чтобы решение системы уравнений (1.75), соответствующее новому базису (1.79), являлось псевдопланом, необходимо, чтобы оценки всех небазисных векторов были неотрицательны.
Ранее было выведено выражение, связывающее оценки векторов в соседних базисах:
j j |
xrj |
s . |
(1.81) |
|
|||
|
xrs |
|
|
На основе этого выражения ответим на вопрос: при каких условиях новые оценки векторов будут неотрицательными?
Ввиду того, что "старому" базису (1.78) соответствует псевдоплан, имеет место s 0 .
Рассмотрим новую оценку вектора Air :
i |
= i |
|
xrir |
s . |
|
xrs |
|||||
r |
r |
|
|
||
|
|
|
Здесь
s 0 , так как старому базису (1.78) соответствует псевдо-
план;
ir 0 , так как это оценка базисного вектора; xrir 1, так как вектор Air входит в старый базис.
Таким образом, требование неотрицательности оценки вектора Air в новом базисе (1.79) эквивалентно выполнению следующе-
го соотношения:
x1 s 0 .
rs
105
Очевидно, что это условие будет выполняться только в том случае, когда имеет место xrs<0.
Условие неотрицательности оценок всех остальных векторов в новом базисе (1.76), учитывая (1.78), можно записать следующим образом:
j |
xrj |
|
s . |
(1.82) |
xrs |
|
|||
|
|
|
|
|
Это условие автоматически выполняется для всех xrj 0 , так |
||||
как j 0 (старая оценка вектора Aj ), |
s 0 и xrs<0. |
|||
В том же случае, когда |
xrj 0 , |
условие (1.82) выполняется |
||
только тогда, когда имеет место (1.80). Теорема доказана. Определим условия, обеспечивающие новому псевдоплану
меньшее значение целевой функции.
ТЕОРЕМА 1.10 (о переходе к лучшему псевдоплану).
Если номера выводимого из базиса (1.78) вектора Air и вво-
димого в базис вектора As таковы, что xrs<0, и выполняются
соотношения (1.82), то новому псевдоплану будет соответствовать лучшее (меньшее) значение целевой функции, если будет иметь место xr0<0.
Доказательство. Используем известное выражение, связывающее значения целевой функции в двух последовательных базисах:
|
Zнов Zст |
xr 0 |
s . |
(1.83) |
|
|
xrs |
||||
|
|
|
|
|
|
Отсюда видно, |
что при |
|
s |
0 , учитывая, что обязательно |
|
должно выполняться |
xrs<0, |
требуемое соотношение |
Zнов Zст |
||
будет выполняться только в том случае, если xr0<0, что и требо-
валось доказать.
Наконец, последний случай оформим в виде следующей теоремы.
ТЕОРЕМА 1.11 (о недопустимости задачи линейного программирования в двойственном симплекс-методе).
Пусть среди коэффициентов разложения вектора A0 по ба-
зису некоторого псевдоплана имеется отрицательный коэффици-
106

ент |
x |
, но все |
x |
0 , |
k 1,2,...,m |
, |
j 1,2,...,n. Тогда задача не |
|
|
k 0 |
|
kj |
|
|
|
|
|
имеет допустимых решений.
Доказательство. Рассмотрим k-ю строку симплекс-таблицы. В этой строке, фактически, записано следующее уравнение, которому должны удовлетворять переменные задачи:
xk0=xk1x1+ xk2x2+... xknxn. (1.84)
Предположим, от противного, что задача имеет допустимое решение x x1, x2 ,..., xn . Подставим координаты этого решения в уравнение (1.84):
|
xk 0 xk1x1 xk 2 x2 |
... xkn xn . |
(1.85) |
||
Ввиду |
того, что все |
x j 0, ( j |
|
) , |
т.к. решение |
1, n |
|||||
x x1, x2 ,..., xn |
– допустимое и все xkj 0 по условию теоремы, в |
||||
правой части (1.85) записано неотрицательное число. В левой же части записано число отрицательное, так как по условию теоремы
xk 0 0 . Полученное противоречие говорит о неправомерности
предположения о том, что задача имеет допустимое решение. Теорема доказана.
1.3.7. Алгоритм двойственного симплекс-метода
Пусть дана задача линейного программирования :
c, x max |
|
|
AX A0 |
|
|
|
x 0, |
|
|
имеющая псевдоплан x x1, x2 ,..., xn , и B Ai1 , Ai2 ,..., Aim - базис
этого псевдоплана.
Алгоритм двойственного симплекс-метода рассмотрим по
шагам.
Шаг 0. Как и в симплекс-методе, найдем коэффициенты разложения всех (небазисных) векторов по базису B , т.е. все элементы симплекс-таблицы xij (i = 1,m; j = 0,n) . Запишем эти коэффициен-
107

ты в первую симплекс-таблицу, после чего вычислим оценкиj ( j 1,2,...,n) и значение целевой функции Z0 .
Шаг 1. Если все xk 0 xik 0,(k = 1,m) , конец, получено оптималь-
ное решение задачи. В противном случае выполняется следующий шаг.
Шаг 2. Поочередно |
просматриваем |
все элементы xkj , |
для |
||
которых xk 0 0. Если обнаруживается, что для некоторого xk 0 |
0 |
||||
все xkj 0, ( j |
|
|
– конец, задача не имеет допустимых решений. |
||
1, n) |
|||||
В противном случае выполняется следующий шаг.
r 0 |
0 |
(r |
|
|
Шаг 3. Выбирается один из коэффициентов x |
|
1,2,...,m ) |
, желательно, максимальный по абсолютной величине (это, как
правило, приводит к ускорению решения задачи). Далее для всех xrj 0, ( j 1,2,...,n ) вычисляются отношения j 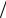 xrj . Из этих
xrj . Из этих
отношений выбирается минимальное по абсолютной величине. Пусть это будет s 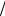 xrs , что соответствует вектору As.
xrs , что соответствует вектору As.
Шаг 4. Переходим к новому псевдоплану с новым базисом: базисный вектор Air заменяется свободным вектором As. С использова-
нием основных формул пересчитываются коэффициенты разложения всех векторов, вычисляются новые оценки свободных векторов и новое значение целевой функции. Далее выполняется шаг 1.
Работу по приведенному алгоритму рассмотрим на примере.
Пример 1.20
Дана задача линейного программирования в канонической форме:
2x |
8x |
2 |
x |
2x |
4 |
2x |
5 |
max |
||||
1 |
|
|
|
3 |
|
|
|
|
|
|||
2x |
4x |
2 |
x |
3 |
|
|
|
|
|
|
= 4 |
|
1 |
|
|
|
|
|
|
|
|
|
|||
x |
x |
2 |
|
|
x |
4 |
|
|
|
= 8 |
||
1 |
|
|
|
|
|
|
|
|
|
|||
3x |
4x |
2 |
|
|
|
|
x |
5 |
=8 |
|||
1 |
|
|
0, j |
|
|
. |
|
|
||||
|
|
|
|
|
|
|||||||
|
xj |
1,4 |
|
|
|
|||||||
108

Умножим левую и правую часть третьего уравнения на "-1":
2x |
8x |
2 |
|
x |
3 |
2x |
4 |
2x |
5 |
max |
|
1 |
|
|
|
|
|
|
|||||
2x |
4x |
2 |
x |
3 |
|
|
|
|
= 4 |
||
1 |
|
|
|
|
|
|
|
|
|
||
x |
x |
2 |
|
|
x |
4 |
|
|
= 8 |
||
1 |
|
|
|
|
|
|
|
|
|
||
3x |
4x |
2 |
|
|
|
|
|
x |
5 |
= 8 |
|
1 |
|
|
|
|
|
|
|
|
|
||
xj 0, ( j 1,4).
В системе ограничений этой задачи имеется полный набор единичных векторов A3, A4 и A5, который является базисом очевидного
решения системы уравнений-ограничений x 0, 0, 4, 8, 8 . Если это
решение – псевдоплан, то можно использовать двойственный симплексметод.
Заполним первую симплекс-таблицу. Коэффициенты разложения всех векторов по базису (единичному) известны, поэтому требуется по известным правилам симплекс-метода лишь вычислить оценки и значение целевой функции.
Баз |
Cбаз |
Ao |
2 |
8 |
1 |
2 |
-2 |
|
|
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A3 |
1 |
4 |
-2 |
4 |
1 |
0 |
0 |
|
A4 |
|
|
|
-1 |
|
|
|
|
2 |
8 |
1 |
0 |
1 |
0 |
|||
A5 |
-2 |
-8 |
-3 |
-4 |
0 |
0 |
1 |
|
Табл.1 |
|
|
|
|
2 |
|
|
|
|
36 |
4 |
0 |
0 |
0 |
|||
Как видно из таблицы, записанное в ней решение является псевдопланом, так как среди оценок векторов нет отрицательных. Решение не является оптимальном, так как в столбце A0 имеется отрицатель-
ный элемент x30 8 .
Признака недопустимости задачи также нет, так как среди коэффициентов третьей строки есть отрицательные x31 , x32 0 , следова-
тельно, решение можно продолжить. Из базиса будет выводиться вектор A5 .
Для того же, чтобы решить вопрос, какой вектор следует вводить в базис, необходимо для всех векторов, имеющие отрицательные коэффициенты в третьей строке (в нашем случае это векторы A1 и A2), вы-
числить отношения 1 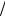 x31 4
x31 4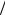 3 – для вектора A1 и 3
3 – для вектора A1 и 3 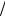 x32 2
x32 2 4 – для вектора A2 . Минимальное из этих отношений соответствует век-
4 – для вектора A2 . Минимальное из этих отношений соответствует век-
тору A2 , следовательно, этот вектор нужно вводить в базис вместо век-
109
тора A5 .
По правилам обычного симплекс-метода, приняв в качестве ве-
дущего элемента коэффициент |
x32 4 , |
формируем новую (вторую) |
|||||||||||
симплекстаблицу. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Баз |
|
Cбаз |
|
Ao |
|
2 |
8 |
|
1 |
2 |
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
A2 |
|
A3 |
A4 |
A5 |
|
|
A3 |
|
1 |
|
-4 |
|
-5 |
0 |
|
1 |
0 |
1 |
|
|
A4 |
|
2 |
|
10 |
|
7/4 |
0 |
|
0 |
1 |
-1/4 |
|
|
A2 |
|
8 |
|
2 |
|
3/4 |
1 |
|
0 |
0 |
-1/4 |
|
|
Табл.2 |
|
|
|
32 |
|
5/2 |
0 |
|
0 |
0 |
1/2 |
|
Новый псевдоплан не является оптимальным решением, так как в |
|||||||||||||
столбце A0 имеется отрицательный элемент x10 |
4 . Признака недо- |
||||||||||||
пустимости задачи также нет, |
так как среди коэффициентов первой |
||||||||||||
строки есть отрицательные |
x11 |
0 , следовательно, |
решение можно |
||||||||||
продолжить. Из базиса будет выводиться вектор A3 . |
В базис может |
||||||||||||
быть введен только вектор A1, так как это – единственный вектор, имеющий отрицательный коэффициент (-5) в третьей строке.
Новая симплекс-таблица (третья): |
|
|
|
|
|
|||||||
Баз |
|
|
|
|
|
|
1 |
|
|
|
|
|
Cбаз |
|
Ao |
2 |
|
8 |
2 |
|
-2 |
||||
|
|
|
|
|
|
|
|
A3 |
|
|
|
|
|
|
|
|
|
A1 |
|
A2 |
A4 |
|
A5 |
|
|
A1 |
2 |
|
4/5 |
1 |
|
0 |
-1/5 |
0 |
|
-1/5 |
|
|
A4 |
2 |
|
43/5 |
0 |
|
0 |
7/20 |
1 |
|
1/10 |
|
|
A2 |
8 |
|
7/5 |
0 |
|
1 |
3/20 |
0 |
|
-1/10 |
|
|
Табл.3 |
|
|
|
30 |
0 |
|
0 |
1/2 |
0 |
|
1 |
|
Получено |
оптимальное |
решение |
задачи, |
так как |
очередной |
|||||||
псевдоплан является допустимым: в столбце A0 нет отрицательных
элементов.
Zопт=30, Xопт=(4/5,7/5,0.43/5,0).
1.3.8. Определение исходного псевдоплана
При использовании двойственного симплекс-метода основные вычислительные сложности связаны с определением исходного псевдоплана. Однако двойственный симплекс-метод в части основной вычислительной процедуры считается более экономным, чем обычный симплекс-метод.
110
