
Жолобов Ввведение в Математическое 2008
.pdf
темы: векторы А3 и А4 оставляют полный единичный базис, которому соответствует опорное решение x*=(0,0,8/3,10/3).
Заполним первую симплекс-таблицу коэффициентами разложения всех векторов по базису В=(А3 , А4)=Е. Эти коэффициенты запишем в левые верхние углы соответствующих клеток таблицы.
Баз |
Cбаз |
A0 |
5 |
|
4 |
|
|
-4 |
|
-9 |
|
|||||
A1 |
A 2 |
|
A 3 |
|
A 4 |
|||||||||||
A 3 |
-4 |
8/3 |
|
|
2/3 |
|
|
1/3 |
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A4 |
-9 |
10/3 |
|
|
1/3 |
|
|
2/3 |
|
|
0 |
|
|
1 |
|
|
|
|
|
5 |
|
|
1/2 |
|
|
1 |
|
|
0 |
|
|
3/2 |
|
Tабл.1 |
|
-122/ 3 |
|
-32/ 3 |
|
-34/ 3 |
|
0 |
|
|
0 |
|
||||
Вычислим значение целевой функции. Для этого попарно перемножим элементы столбцов Cбаз и A0 и сложим полученные произведения:
Z0= -4 (8/3) -9 (10/3)=-122/3.
Фактически, получено скалярное произведение двух векторов:
Cбаз=(с3,с4)=(-4,-9) и X0=(x10 ,x20)=(8/3,10/3).
Для вычисления оценок j (j=1,2,...,n) используется тот же прием: вычисляется скалярное произведение векторов Cбаз=(с3,с4) и Xj=(x1 j , x2 j), а затем из полученного произведения вычитается cj .
Так, например, оценки векторов A1 и A2 подсчитываются следующим образом:
1 =-4 (2/3) - 9 (1/3) - 5 =-32/3
2 =-4 (1/3) - 9 (2/3) - 4 =-34/3.
Наличие отрицательных оценок свидетельствует о том, что рассматриваемое опорное решение не является оптимальным.
Вкаждом столбце с отрицательной оценкой имеются положительные элементы, поэтому нет основания для принятия решения о неограниченности целевой функции сверху: решение можно улучшить путем введения в базис вектора с отрицательной оценкой.
Из двух таких векторов A1 и A2 выбираем вектор A2 , обладающий наибольшей по абсолютной величине отрицательной оценкой.
Следует отметить, что выбор вектора A1 не приведет к ошибке: и
втом, и в другом случае будет получено лучшее опорное решение.
Встолбце A2 есть два положительных элемента: x12 и x22. Следовательно, для того чтобы принять решение, какой вектор выводить из базиса (A3 или A4), необходимо вычислить отношения:
x10 |
|
8 / 3 |
=8 ; |
x20 |
|
10 / 3 |
=5. |
|
x |
1 / 3 |
|
2 / 3 |
|||||
|
|
x |
22 |
|
|
|||
12 |
|
|
|
|
|
|
|
|
Минимальное отношение соответствует вектору A4 – его нужно вывести из базиса.
Начинаем пересчет координат разложения векторов по новому
51

базису, а также нового значения целевой функции и оценок. Пересчет проводится в следующем порядке:
Вычисляются вторые координаты всех векторов. Для этого вторая строка таблицы делится на ведущий элемент (в нашем случае это эле-
мент x22 = 2/3).
Результат деления записывается непосредственно в эту же строку (в правый нижний угол соответствующих клеток таблицы).
Эти же данные записываются во вторую строку новой симплекстаблицы. Для вычисления всех остальных координат, нового значения целевой функции и оценок используется правило “крест-накрест”. Результаты записываются в новую таблицу.
Баз |
Cбаз |
A0 |
5 |
|
|
4 |
|
|
-4 |
|
-9 |
|
||||
A1 |
|
A 2 |
|
A 3 |
A 4 |
|||||||||||
A 3 |
-4 |
1 |
|
|
1/ 2 |
0 |
|
|
1 |
|
|
-1/ 2 |
|
|||
|
|
|
2 |
|
|
1 |
|
|
0 |
|
|
2 |
|
|
-1 |
|
A2 |
4 |
5 |
|
|
1/ 2 |
|
1 |
|
|
0 |
|
|
3/ 2 |
|
||
Табл.2 |
|
16 |
|
-5 |
|
|
0 |
|
|
0 |
|
|
17 |
|
||
Начинаем анализ нового опорного решения x*=(0,5,1,0).
В базис вводится вектор A1 , имеющий отрицательную оценку, а выводится вектор A3 , так как этому вектору соответствует минимальное отношение:
x10 |
|
|
1 |
=2 < |
x20 |
|
|
5 |
=10. |
|
x |
|
1 / 2 |
|
x |
21 |
|
1 / 2 |
|
||
11 |
|
|
|
|
|
|
|
|
|
|
Третья симплекс-таблица.
|
|
|
5 |
4 |
-4 |
-9 |
Баз |
Cбаз |
A0 |
A1 |
A 2 |
A 3 |
A 4 |
A 1 |
5 |
2 |
1 |
0 |
2 |
-1 |
A2 |
4 |
4 |
0 |
1 |
-1 |
2 |
Табл.3 |
|
26 |
0 |
0 |
10 |
12 |
|
|
|
|
|
|
|
Все оценки неотрицательны, следовательно, получено оптимальное решение:
x*=(2,4,0,0); Zопт.= 26.
Разберем еще один пример решения задачи симплексметодом.
52

Пример 1.10
Решить симплекс-методом следующую задачу линейного программирования:
2x1 |
+ x2 |
- 5x3 |
-x4 |
- x5 |
|
max |
x1 |
-x2 |
+ x3 |
+ x4 |
|
= |
5 |
-x1 |
-x2 |
+ x3 |
|
+ x5 |
= |
1 |
xj 0, j=1 5.
Решение этой задачи представлено ниже двумя симплекстаблицами. На второй итерации срабатывает признак неограниченности
целевой функции: вектор A2 |
имеет отрицательную оценку, а среди ко- |
|||||||||
ординат разложения этого вектора по базису ( |
A1, A5 ) нет ни одной |
|||||||||
положительной координаты. |
|
|
|
|
|
|
|
|
||
Целевая функция задачи не ограничена сверху на допустимом |
||||||||||
множестве. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Баз |
Cбаз |
A0 |
2 |
1 |
-5 |
|
-1 |
-1 |
|
|
A1 |
A2 |
A3 |
|
A4 |
A5 |
|
|||
|
A4 |
-1 |
5 |
1 |
-1 |
1 |
|
1 |
0 |
|
|
A5 |
-1 |
1 |
-1 |
-1 |
1 |
|
0 |
1 |
|
|
Tабл.1 |
|
-6 |
-2 |
1 |
3 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
-5 |
|
-1 |
-1 |
|
|
Баз |
Cбаз |
A0 |
A1 |
A2 |
A3 |
|
A4 |
A5 |
|
|
A1 |
2 |
5 |
1 |
-1 |
1 |
|
1 |
0 |
|
|
A5 |
-1 |
6 |
0 |
-2 |
2 |
|
1 |
1 |
|
|
Табл.2 |
|
4 |
0 |
-1 |
5 |
|
2 |
0 |
|
1.2.11. Симплекс-метод в общем случае
До сих пор рассматривался случай невырожденной задачи линейного программирования. Рассмотрим общий случай.
Пусть дана задача, в которой возможны вырожденные опорные решения:
c, x max, |
|
A1 x1 A2 x2 |
... An xn A0 , |
|
x 0. |
причем, ранг матрицы |
A = (A1, A2, …, An) равен, по- |
прежнему, m – количеству ограничений-уравнений. Предположим сначала, что имеется некоторое опорное реше-
ние x (x1, x2 ,..., xn )
и базис этого решения:
53

B = ( Ai1 , Ai2 ,..., Aim ), ik {1,2,...,n}.
Пусть далее не выполняется ни условие оптимальности этого решения, ни условие неограниченности целевой функции сверху на допустимом множестве.
Возьмем любой вектор AS , имеющий отрицательную оценку:
s 0, |
(s {1,2,..., n}; |
s {i1 ,i2 ,...,im }). |
|||
|
|
|
|
|
|
Предположим, что |
0 |
min |
xk 0 |
. |
|
|
|||||
|
|
xks 0 xks |
|
|
|
Для невырожденной задачи линейного программирования существует единственный базисный вектор, которому соответст-
вует 0.
Замена в базисе именно этого вектора небазисным вектором AS гарантирует, что новому базису будет соответствовать опорное решение, и оно будет невырожденным. Если же таких векторов несколько, новое опорное решение будет вырожденным.
Действительно, пусть
|
|
|
|
xr 0 |
|
xl 0 |
|
|
|
0 |
min |
xk 0 |
|
|
|
, |
(r,l {1,2,...,m},r l) . |
||
|
xrs |
|
|||||||
|
xks 0 xks |
|
|
|
xls |
|
|||
Заменим базисный вектор |
Ai вектором AS ( s <0). |
||||||||
|
|
|
|
|
|
|
r |
|
|
Используя основные формулы, вычислим значение l-й координаты в разложении вектора A0 по новому базису:
x |
x |
|
xr 0 |
x |
x |
|
xl 0 |
x |
ls |
0 . |
|
|
|||||||||
l 0 |
l 0 |
|
|
ls |
l 0 |
|
xls |
|
||
|
|
|
xrs |
|
|
|
|
|||
Таким образом, в новом опорном решении появилась базисная переменная, имеющая нулевое значение.
Пусть теперь имеется некоторое вырожденное опорное решение x (x1, x2 ,..., xn ) , в котором, для определенности, отличными от
нуля переменными являются первые l переменные (l < m), а остальные имеют нулевое значение.
Пусть базис этого решения составляют векторы A1, A2, …, Am . Пусть далее не выполняется ни условие оптимальности этого решения, ни условие неограниченности целевой функции сверху на
допустимом множестве.
54

На рис.1.11 представлен фрагмент соответствующей сим- плекс-таблицы.
Баз |
Сбаз |
А0 |
|
|
cs |
|
|
cn |
|
|
|||||||
|
c1 |
|
|
|
Аs |
|
|
Аn |
|
|
|
|
|
||||
A1 |
x10 |
|
|
xs1 |
|
|
x1n |
|
|
|
|
||||||
A2 |
c2 |
x20 |
|
|
xs2 |
|
|
x2n |
|
|
|
||||||
|
cl |
|
|
|
|
|
|
|
Al |
xl0 |
|
|
xs3 |
|
|
xln |
|
|
|
|
|
|||||
Al+1 |
cl+1 |
0 |
|
|
xl+1,s |
|
|
xl+1,n |
|
cm |
|
|
|
|
|
|
|
Am |
0 |
|
|
xms |
|
|
xmn |
|
|
|
|
|
|||||
|
|
Z0 |
|
|
s |
|
|
n |
Рис.1.11. Симплекс-таблица вырожденной задачи
Возьмем любой вектор Аs , имеющий отрицательную оценку:
s<0, s {1,2,...,n}.
Предположим, что среди элементов xl+1,s, xl+2,s, …, xms есть положительный элемент xrs > 0, где r {l+1,l+2,...,m}. Тогда, учи-
тывая, что xl+1,0= xl+2,0= … = xm0=0 :
|
|
|
|
|
xr0 |
|
|
0 |
min |
xk 0 |
|
|
0. |
||
|
xrs |
||||||
|
xks 0 |
xks |
|
|
|
||
Найдем базисные координаты опорного решения, которое будет соответствовать новому базису (этот базис образуется заменой базисного вектора Ar свободным вектором As):
|
|
xr 0 |
|
|
0 |
|
|
|
|
|
|
|
xko xk 0 |
|
|
xks xk 0 |
|
|
xks xk 0 |
, k 1,2,...,m; k r; |
|||||
xrs |
xrs |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
xr 0 |
|
|
0 |
|
|
|
|
|
|
|
xro |
|
|
|
|
|
0. |
|
|
|
|
|
|
xrs |
|
xrs |
|||||
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, в новой симплекс-таблице столбец A0 не из-
менился – новое опорное решение совпадает со старым. Не изме-
нилось и значение целевой функции:
55
z z |
xr 0 |
s z |
0 |
s z , |
|
|
|||
|
xrs |
xrs |
||
т.е. лучшее значение целевой функции не получено. Однако новому базису, в общем случае, соответствует новая симплекс-таблица: в ней записаны новые коэффициенты разложения векторов
A1, A2, …, An.
Изменились и оценки свободных векторов. Теперь может возникнуть одна из трех ситуаций:
1. Получено оптимальное решение (нет отрицательных оце-
нок);
2.Целевая функция не ограничена сверху на допустимом множестве;
3.Решение следует продолжить.
В третьем случае, возможно, снова не удастся улучшить значение целевой функции.
Ввиду того, что количество базисов, соответствующих опорным решениям любой задачи линейного программирования, конечно, после некоторого числа переходов от одного опорного решения к другому, в принципе, возможно возникновение четвертой ситуации, а именно, очередное опорное решение будет иметь базис, который фигурировал ранее.
Такая ситуация называется зацикливанием. В настоящее время разработан целый ряд способов защиты от зацикливания. Рассмотрим наиболее известный из них.
1.2.12. Лексикографический симплекс-метод
Рассмотрим подробнее эффект зацикливания на примере. Решим следующую задачу линейного программирования.
Пример 1.11
300x5 80x6 |
|
1219x7 |
x8 |
max |
|||||||||||||
x |
|
8x |
|
2x |
|
30x |
|
1 |
|
x |
0 |
||||||
|
2 |
|
5 |
|
|
|
6 |
|
|
|
7 |
|
2 |
8 |
|
|
|
x 19 |
2 |
x |
|
|
5 |
x |
|
38x |
|
|
2 |
x 0 |
|||||
1 |
|
|
5 |
|
|
2 |
|
6 |
|
|
|
7 |
|
3 |
8 |
||
x3 40x5 3x6 90x7 |
x8 |
1 |
|
||||||||||||||
x4 |
x8 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Условимся всегда вводить в базис первый в таблице вектор с отри-
56
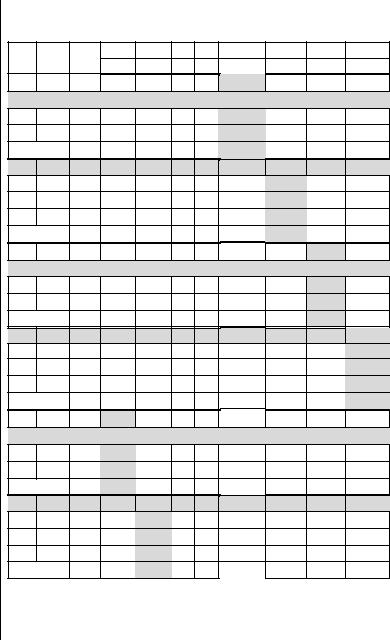
цательной оценкой, считая от начала, при наличии альтернатив всегда |
|||||||||||
выводить из базиса первый вектор, считая сверху таблицы. В этом случае |
|||||||||||
процедура решения задачи выглядит следующим образом. |
|
|
|||||||||
Баз |
Cбаз |
A0 |
0 |
0 |
0 |
0 |
300 |
80 |
-1219 |
-1 |
|
A1 |
A2 |
A3 A4 |
A5 |
A6 |
A7 |
A8 |
|||||
|
|
|
|||||||||
A2 |
0 |
0 |
0 |
1 |
0 |
0 |
-8 |
-2 |
30 |
1/2 |
|
A1 |
0 |
0 |
1 |
0 |
0 |
0 |
19/2 |
5/2 |
-38 |
-2/3 |
|
A3 |
0 |
1 |
0 |
0 |
1 |
0 |
40 |
-3 |
90 |
1 |
|
A4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
Tабл.1 |
0 |
0 |
0 |
0 |
0 |
-300 |
-80 |
1219 |
1 |
||
A2 |
0 |
0 |
16/19 |
1 |
0 |
0 |
0 |
2/19 |
-2 |
-7/114 |
|
A5 |
300 |
0 |
2/19 |
0 |
0 |
0 |
1 |
5/19 |
-4 |
-4/57 |
|
A3 |
0 |
1 |
-80/19 |
0 |
1 |
0 |
0 |
-257/19 |
250 |
217/57 |
|
A4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
Табл.2 |
0 |
600/19 |
0 |
0 |
0 |
0 |
-20/19 |
19 |
-1143/57 |
||
A6 |
80 |
0 |
8 |
19/2 |
0 |
0 |
0 |
1 |
-19 |
-7/12 |
|
A5 |
300 |
0 |
-2 |
-5/2 |
0 |
0 |
1 |
0 |
1 |
1/12 |
|
A3 |
0 |
1 |
104 |
257/2 |
1 |
0 |
0 |
0 |
-7 |
-49/12 |
|
A4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
Табл.3 |
0 |
40 |
10 |
0 |
0 |
0 |
0 |
-1 |
-62/3 |
||
A6 |
80 |
0 |
-30 |
-38 |
0 |
0 |
19 |
1 |
0 |
1 |
|
A7 |
-1219 |
0 |
-2 |
-5/2 |
0 |
0 |
1 |
0 |
1 |
1/12 |
|
A3 |
0 |
1 |
90 |
111 |
1 |
0 |
7 |
0 |
0 |
-7/2 |
|
A4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
Табл.4 |
0 |
38 |
15/2 |
0 |
0 |
1 |
0 |
0 |
-247/12 |
||
A8 |
-1 |
0 |
-30 |
-38 |
0 |
0 |
19 |
1 |
0 |
1 |
|
A7 |
-1219 |
0 |
1/2 |
2/3 |
0 |
0 |
-7/12 |
-1/12 |
1 |
0 |
|
A3 |
0 |
1 |
-15 |
-22 |
1 |
0 |
147/2 |
7/2 |
0 |
0 |
|
A4 |
0 |
1 |
30 |
38 |
0 |
1 |
-19 |
-1 |
0 |
0 |
|
Табл.5 |
0 |
-1159/2 |
|
0 |
0 |
4705/12 |
247/12 |
0 |
0 |
||
A8 |
-1 |
0 |
0 |
2 |
0 |
0 |
-16 |
-4 |
60 |
1 |
|
A1 |
0 |
1 |
1 |
4/3 |
0 |
0 |
-7/6 |
-1/6 |
2 |
0 |
|
A3 |
0 |
0 |
0 |
-2 |
1 |
0 |
-56 |
1 |
30 |
0 |
|
A4 |
0 |
0 |
0 |
-2 |
0 |
1 |
16 |
4 |
-60 |
0 |
|
Табл.6 |
0 |
0 |
-2 |
0 |
0 |
-284 |
-76 |
1159 |
0 |
||
|
|
|
|
|
57 |
|
|
|
|
|
|

A2 |
0 |
0 |
0 |
1 |
0 |
0 |
-8 |
-2 |
30 |
1/2 |
A1 |
0 |
0 |
1 |
0 |
0 |
0 |
19/2 |
5/2 |
-38 |
-2/3 |
A3 |
0 |
1 |
0 |
0 |
1 |
0 |
40 |
-3 |
90 |
1 |
A4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
Табл.7 |
0 |
0 |
0 |
0 |
0 |
-300 |
-80 |
1219 |
1 |
|
Табл. 7 полностью эквивалентна табл. 1 – произошло зациклива-
ние.
Одним из наиболее простых и эффективных способов защиты от зацикливания является лексикографический метод. Для его обоснования введем ряд определений.
Вектор q – лексикографически положителен ( q 0), если его
первый отличный от нуля элемент положителен
Вектор q лексикографически больше вектора p ( q p ), если q p 0 . Из этого определения автоматически следует, что если p
– некоторый вектор, а q – лексикографически положительный вектор, тогда p q p.
Вектор q j лексикографически минимальный среди множества векторов q1,...,qN , если q j все векторы этого множества за исключением самого q j лексикографически больше вектора q j . Это условие записывается как q j lex min q1 ,..., qN .
Рассмотрим векторы, получаемые из строк симплекс-
таблицы: Sk (xk 0 , xk1 ,...xkn ).
Симплекс-таблицу, все строки которой лексикографически положительны ( Sk 0 ), будем называть лексикографически до-
пустимой.
Лексикографически допустимая симплекс-таблица получается из произвольной путем перенумерации столбцов – например, если перенумеровать базисные векторы так, чтобы им соответствовали первые m столбцов симплекс-таблицы, то новая симплекс-таблица будет лексикографически допустимой.
Пусть имеется лексикографически допустимая симплекс таблица, в которой не срабатывает ни признак оптимальности, ни признак неограниченности сверху целевой функции, т.е. имеется вектор As с отрицательной оценкой s 0 . Рассмотрим следующие
58
векторы, |
|
получающиеся из |
строк этой симплекс таблицы: |
||||||||
S |
k |
( |
xk 0 |
, |
xk1 |
,..., |
xkn |
) |
(для всех x |
|
0 ). |
|
|
|
|
||||||||
|
|
xks |
|
xks |
xks |
ks |
|
||||
|
|
|
|
|
|
|
|||||
ЛЕММА 1.2. Если симплекс-таблица лексикографически допустима, а номера вводимого и выводимого из базиса векторов таковы, что выполняется условие
Sr |
( |
xr 0 |
, |
xr1 |
,..., |
xrn |
) lex min{Sk }, |
(1.49) |
|
xrs |
xrs |
xrs |
|||||||
|
|
|
|
xks 0 |
|
||||
|
|
|
|
|
|
|
|
то новая симплекс-таблица будет также лексикографически допустимой.
Доказательство. Из того факта, что xrs 0, следует лексикографическая положительность вектора Sr . Заменим в базисе вектор Ar
соответствующий этому вектору Sr на вектор As . Запишем основные формулы пересчета коэффициентов в векторном виде:
Sr Sr |
|
(1.50) |
||
S S |
k |
S |
x |
(1.51) |
k |
r |
ks |
|
|
Из (1.50) следует, что S 0 , т.е. строка r новой симплекстаблицы лексикографически положительна. Рассмотрим (1.51). Если xks 0 , то автоматически Sk 0 , поскольку она получается из
суммы двух лексикографически положительных строк.
Если xks 0 , то перепишем (1.51) в следующем виде:
|
S |
|
xks Sk Sr . Из (1.49) следует, что вектор в |
Sk xks |
k |
Sr |
|
x |
|||
|
ks |
|
|
скобках лексикографически положителен, а значит строка k новой симплекс-таблицы лексикографически положительна при любых xks , что и требовалось доказать.
ТЕОРЕМА 1.5. Если на каждом шаге симплекс-метода при выборе вводимого и выводимого из базиса векторов выполняется условие (1.49), то количество шагов, которое необходимо осуществить до остановки по признаку оптимальности или неограниченности целевой функции сверху, конечно.
59
Доказательство. Рассмотрим вектор, получаемый из строки с оценками D ( 1 ,..., n ) . При переходе к новому опорному реше-
нию этот вектор пересчитывается по следующей формуле: D D Sr s . Поскольку s 0 , а Sr –всегда лексикографически
положителен, то для каждого шага симплекс-метода D D . Однако неравенство типа «лексикографическое больше» является строгим, а поэтому при выполнении условия (1.49) невозможен возврат к предыдущему базису (это означало бы, что на каком-то из шагов
выполняется условие D D ). Теорема доказана.
Сформулируем алгоритм лексикографического симплексметода по шагам.
Шаг 0. Привести симплекс-таблицу к лексикографически допустимому виду.
Шаг 1. Пусть
|
|
x |
|
|
xq 0 |
|
xq 0 |
|
xq 0 |
|
|
0 |
min |
k 0 |
|
|
1 |
|
2 |
... |
t |
, |
|
|
xq1s |
xq2s |
xqt s |
||||||||
|
xks 0 |
xks |
|
|
|
|
|
||||
т.е. имеется t базисных векторов, каждый из которых может быть заменен небазисным вектором As . Если t=1, из базиса выво-
дится вектор Aq1 . В противном случае производится вычисление:
Шаг 2.
1 |
x |
k1 |
|
|
xq 1 |
|
xq 1 |
|
xqp 1 |
|
|
min |
|
|
|
1 |
|
2 |
... |
|
, |
||
|
|
xq1s |
xq2 s |
xqp s |
|||||||
|
xks 0 xks |
|
|
|
|
|
|||||
т.е. вместо вектора A0 используется вектор A1 .
Теперь имеется p базисных векторов, каждый из которых может быть заменен небазисным вектором As . Если q=1, из базиса
выводится вектор Aq1 . В противном случае производится анало-
гичные вычисление, но уже с использованием вектора A2 (шаг 3), и так далее. В итоге, учитывая то обстоятельство, что в симплекстаблице каждая строка отличается от любой другой, по крайней мере, одним коэффициентом, будет найден единственный вектор, который нужно вывести из базиса.
Рассмотрим работу этого правила на примере 1.11.
60
