14-es / Высшая математика (РТФ) / умк_Вакульчик_Элементы линейной алгебры

Определение 2.20.8. Если в точке x0 нарушено хотя бы одно из ус- ловий непрерывности, то она называется точкой разрыва.

Замечания:

1.Можно доказать, что все три определения непрерывности в точке эквивалентны.

2.Для исследования функции на непрерывность наиболее удобным является определение 2.20.7.

3.Для непрерывной в точке x0 функции символы функции и преде-

ронних предела конечны, то x0 – точка разрыва первого рода. Причем, если односторонние пределы равны, x0 – называют точкой устранимого разрыва.

131

и хотя бы один из односторонних пределов бесконечен либо не существу- ет, то x0 – точка разрыва второго рода.

Примеры.

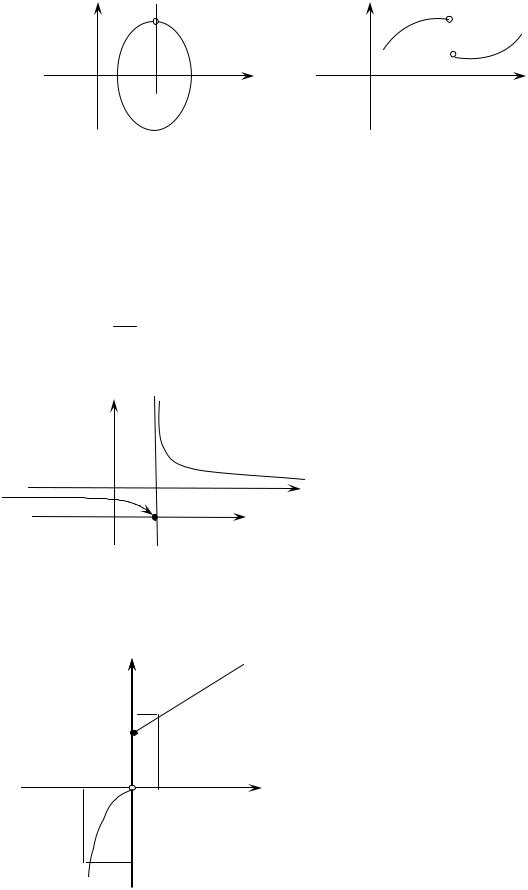
Исследовать на непрерывность функции:

1

10. y = 2 x−5 .

Значит, x = 5 является точкой разрыва второго рода.

132

Теорема 2.21.2. (о непрерывности сложной функции) Если функция

Замечание 2.21.1. Основные элементарные функции непрерывны в области своего определения.

2.22. Свойства функций непрерывных на отрезке

Определение 2.22.1. Функция называется непрерывной на интерва- ле (a, b) , если она непрерывна во всех точках этого интервала.

Определение 2.22.2. Функция называется непрерывной на отрезке [a,b] , если она непрерывна на интервале (a, b) и непрерывна справа в точке a и непрерывна слева в точке b .

достигает на этом отрезке своего наименьшего и наибольшего значений.

Теорема 2.22.3. Если две функции непрерывны на отрезке [a,b] , то

их сумма, произведение, произведение каждой из них на число, а так же частное в точках, где знаменатель не равен нулю, также непрерывны на данном отрезке.

Теорема 2.22.4. (теорема Коши о нулях функции). Пусть функция y = f ( x) непрерывна на отрезке [a,b] , а также принимает значения разных

знаков на его концах ( f (a) × f (b) < 0) , тогда существует хотя бы одна точ-

ка с на отрезке [a,b] , такая что f (c) = 0 .

134

ВЫВОДЫ

Вданном модуле кратко изложены понятия множества и числовых множеств; на их основе введены понятия функции, предела числовой по- следовательности, предела функции, бесконечно малой и бесконечно большой функций. На языке пределов определено фундаментальное поня- тие анализа - непрерывность функции. Изложены правила вычисления пределов, раскрытия неопределенных выражений.

Функция – это закон или соответствие, по которому каждому эле- менту одного множества отвечает один элемент другого множества. Функ- ция может быть задана при помощи формулы, таблицы, графика, компью- терной программы. С помощью функций записывается соответствие меж- ду величинами, определяющими ход некоторого процесса или явления. Правильно составленная функция, изучение и анализ ее графика дают воз- можность более глубоко познать соответствующий процесс, и, следова- тельно, грамотно им управлять, используя при этом соответствующий ма- тематический аппарат.

Понятие предела переменной величины является в анализе основ- ным, оно ассоциируется в нашем сознании с числом, к которому прибли- жается значение переменной величины, оставаясь или меньше этого числа, или больше, или изменяясь, принимая то большие, то меньшие значения. Предельный переход открывает новые возможности изучения процессов с помощью математики, в частности, возможность изучения отношения двух бесконечно малых или бесконечно больших величин.

Вокружающем нас мире процессы и явления, в которых участвуют многочисленные факторы, обычно непрерывны. Непрерывность процесса или явления означает, что бесконечно малые изменения одних величин вы- зывают бесконечно малые изменения других. Таковы процессы изменения количества углекислого газа в вентилируемом помещении, теплообмена в некотором тепловом агрегате, накопления подаваемой с помощью насоса жидкости в резервуаре, роста бактерий, изменения количества вещества при радиоактивном распаде и т.п.

135

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРОВЕДЕНИЮ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

Учебно-информационный блок для проведения практических занятий

Используемая литература

1.Бугров, Я.С. Дифференциальное и интегральное исчисление / Я.С. Бугров, С.М. Никольский. – М. : Наука, 1980.

2.Гусак, А.А. Справочник по высшей математике / А.А. Гусак, Г.М. Гусак. – Мн. : Навука і тэхніка, 1991.

136

3.Методические указания с трехуровневыми заданиями для органи- зации самостоятельной работы студентов всех специальностей по теме «Прямоугольная и полярная системы координат. Функции, заданные пара- метрически» / В.С. Вакульчик, В.А. Жак, О.В. Скоромник. – Новополоцк:

ПГУ, 2004.

4.Мышкис А.Д. Лекции по высшей математике / А.Д. Мышкис. –

М.: Наука, 1973.

5.Сборник задач по математике для втузов. Линейная алгебра и ос- новы математического анализа / под ред. А.В. Ефимова, Б.П. Демидовича. –

М.: Наука, 1986.

I. Основные элементарные функции и их графики. График функции в полярных координатах

1. Основная методическая схема работы по пособию. Беглое повто- рение основных элементарных функций с использованием выданного на предыдущем занятии информационного материала в виде графиков функ- ций. Преподаватель у доски определяет полярную систему координат; об- ращает внимание на связь декартовой и полярной систем координат; стро- ит графики кривых, заданных в полярной системе координат:

1)r = cos3ϕ ;

2)r = a (1 − cos ϕ) ;

3) r = 2 . sin ϕ

2.Провести обобщение полученных графиков относительно клас- сов аналогичных кривых. Обратить внимание на возможность аналитиче- ского построения кривых.

3.Студенты работают с пособием [3] или УМК. Работа осуществля- ется в соответствии с методической схемой II. Обратить внимание на обу- чающие задачи.

Обучающая задача 1. Построить точки в полярной системе коорди-

оси ОР (положительное направление указано стрелкой) и отложим от полю- са в положительном направлении оси ОР1 отрезок ОМ1, равный трем еди- ницам масштаба. Конец этого отрезка и будет искомой точкой М1 (рис. 1).

137

По такому же принципу проведем через полюс О ось ОР1 под углом

3π к полярной оси ОР (положительное направление указано стрелкой) и 4

отложим от полюса в положительном направлении оси ОР1 отрезок ОМ2, равный одной единице масштаба. Конец этого отрезка и будет искомой точкой М2 (рис. 2).

Аналогично, проведем через полюс О ось ОР1 под углом 5π к по- 4

лярной оси (положительное направление на ней указано стрелкой) и от- ложим от полюса в отрицательном направлении оси ОР1 отрезок ОМ3, рав- ный двум единицам масштаба. Конец этого отрезка и будет искомой точ- кой М3 (рис. 3).

жутки π . 12

Решение. Так как левая часть данного уравнения неотрицательна, то угол ϕ может изменяться только в тех пределах, для которых sin 2j ³ 0 ,

т.е. 0 ≤ ϕ ≤ π и π ≤ ϕ ≤ 3π . Для вычисления значения ρ составляем таблицу

Обучающая задача 3. Построить фигуру, ограниченную кривыми

Решение.

1. Рассмотрим кривую ρ = 3cos ϕ . Анализ уравнения позволяет за- метить, что умножение заданного уравнения на ρ позволяет получить уравнение ρ2 = 3ρcos ϕ , которое в прямоугольной системе координат при-

тить, что его удобнее переписать в виде ρcos ϕ = 2 . В прямоугольной сис- теме координат будем иметь x = 2.

3. Построим заданные кривые и выберем ту фигуру, которая не со- держит начало координат.

y

4. Вся аудитория выполняет задание первого уровня сложности.

140