умк_Вакульчик_Элементы линейной алгебры

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

в точках, где ν ( x) ¹ 0 ;

(cu )¢ = cu¢ .

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

5.38 Mб

Скачать

☆

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 3619 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

3. Бесконечная производная, односторонние

1, 2, 3,

производные. Производные и дифференциалы

РП,

5, 4, 6,

высших

порядков.

Применение

дифферен-

ПДЗ

циала в приближенных вычислениях

Основные

теоремы

дифференциального

1, 2, 3,

РП

исчисления (теоремы Ролля, Коши, Лагранжа)

5, 4, 6, 7

5. Применение производной. Правило Ло-

питаля –

Бернулли.

Локальный

экстремум.

1, 2, 3,

ВКР,

Теорема Ферма. Условия возрастания и убы-

5, 4, 6,

РП

вания функций. Достаточные условия локаль-

ного экстремума

6. Выпуклость и вогнутость. Точки переги-

1, 2, 3,

ба. Глобальный экстремум функции. Практи-

ВКР,

VII

5, 4, 6,

ческие задачи на оптимизацию. Приложения

РП

производной к задачам геометрии и физики

Асимптоты графика функции. Общая

1, 2, 3,

ВКР,

схема исследования функции и построение ее

VIII

5, 4, 7,

РП

графика

Формула

Тейлора

для

произвольной

1, 2, 3,

ВКР,

функции с остаточным членом в форме Ла-

РП,

5, 4, 7

гранжа

ПДЗ

Разложение элементарных

функций по

1, 2, 3,

ВКР,

формуле

Тейлора

Маклорена. Формула

5, 4, 7

РП

Тейлора и ее приложения

181

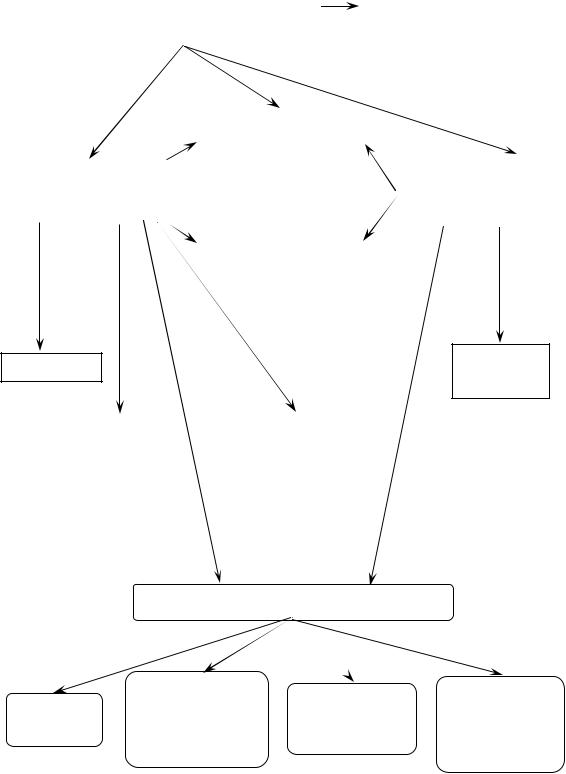
ГРАФИЧЕСКАЯ СХЕМА МОДУЛЯ 3

ДИФФЕРЕНЦИАЛЬНОЕ
ДИФФЕРЕНЦИАЛЬНОЕ		Основные теоремы
ИСЧИСЛЕНИЕ ФУНКЦИИ		Ферма, Ролля,
ОДНОЙ ПЕРЕМЕННОЙ		Лагранжа, Коши

	Производная
	функции, заданной
	неявно
		Производные
Первая


		высших
производная		высших
производная		порядков
	Производная	порядков
	Производная
	функции, заданной
	параметрически

Таблица

Формула

Тейлора

Правила		Логарифмическая
дифференцирования		производная

ПРИЛОЖЕНИЯ

	Дифференциалы	Задачи	Задачи
	первого и
Правило			физики,
		на
Лопиталя	высших		механики и
		оптимизацию
	порядков		т.п.

182

Информационная таблица « Дифференциальные исчисления»

Производной от функции у = у(х) в точке x называется предел приращения функции к приращению аргумента, когда последнее стремится к нулю, если этот предел сущест- вует, конечен и не зависит от способа стрем- ления х к нулю

y¢ = lim Dy

x→0 Dx

Правила дифференцирования

1. c′ = 0 ;	4. (cu )¢ = cu¢ ;
2. (u ± v)¢ = u¢ ± v¢ ; 5.		u ¢	=	u¢v - uv¢
					;

		v		v2

3. (uv)¢ = u¢v + uv¢ ; 6. fx¢(u ( x)) = fu¢ × ux¢ .

Таблица производных

1.(un )¢ = n × un−1 × u¢ ;

2.x′ =1 ;

(

)¢ =

× u¢ ;

степенные

1 ¢

= -

× u¢ ;

(sin u )¢ = cos u × u¢ ;

(cos u )¢ = - sin u × u¢ ;

тригономет

(tg u )¢ =

× u¢

рические y(x0)

cos2

(ctg u )¢ = -

× u

sin2 u

y=kx+b

(au )¢ = au × ln a × u¢ ;

показательные

(eu )¢ = eu

10.

× u¢ ;

11. (loga

u )¢ =

× u

¢ ;

u × ln a

12. (ln u )¢ =

логарифмическые

× u¢ ;

13.

(arcsin u )¢

× u¢ ;

1 - u2

14.

(arccos u )¢ = -

× u¢ ;

обратно

1 - u2

тригоно

15.

(arctg u )¢ =

× u¢ ;

метриче

1 + u

ские

16.

(arcctg u )¢

= -

× u¢ ;

+ u

17.(sh u )¢ = ch u × u¢ ;

18.(ch u )¢ = sh u × u¢ ;


19.	(th u )¢ =		1		× u¢ ; гиперболические
19.	(th u )¢ =	ch2 u			× u¢ ; гиперболические
		ch2 u
20.	(c th u )¢ = -		1			× u¢ .
20.	(c th u )¢ = -			sh2		× u¢ .
				sh2	u

yt¢

(

y¢

y¢¢

) t ,

x = x (t )

x¢

y = y (t )

yx¢ = -

Fx′

if F (x; y) = 0

F ¢

Геометрический смысл производной

производная от функции

y = f ( x)

в точ-

ке

x0 есть тангенс

угла наклона

каса-

тельной, проведённой к графику функции

в точке x : y′( x ) = tg α = k .
		0		0
			y = y ( x		) + y′( x		)( x − x		)
				0		0		0
			–	уравнение касательной.
				y = y ( x0 ) −		1		( x − x0 )
				y = y ( x0 ) −		y′( x0 )		( x − x0 )
						y′( x0 )
x0	x		–	уравнение нормали.
	x		–	уравнение нормали.

Механический смысл производной: про-

изводная от функции S, равная S’(t), где S(t)

– путь, пройденный материальной точкой за время t, есть мгновенная скорость мате- риальной точки в определенный момент времени. S = S(t), vмгн(t0) = S’(t0)

I.Монотонность, экстремум

1. Найти критические точки

y′ = 0	y′ –	не существует

2.	min	max
y'		+	-	-
-
y	x1	x2	x3	x

II. Наибольшее и наименьшее значе- ния

1.Найти критические точки.

2.Вычислить f (x) в критических точ- ках, попавших в отрезок.

3.Вычислить f (x) на концах отрезка Выбрать fнаиб. и fнаим..

183

КРАТКОЕ СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА

3.1. Задачи, приводящие к понятию производной

Рассмотрим следующие задачи:

Задача 1 (о плотности). Пусть m(x) – масса куска тонкого неод- нородного стержня, заключенного между левым концом и произвольной точкой x, лежащей внутри стержня. Требуется найти удельную линейную плотность в произвольной точке стержня.

Решение:

1. Вспомним формулу удельной линейной плотности для однород- ного стержня: ρ = const , тогда

ρ =

(3.1.1)

где m –

масса стержня, а l – его длина.

Пусть плотность стержня равномерно меняется от точки

x1 до

точки x2, тогда

x2 = x1 +

m( x2 ) − m( x1 )

m( x1 +

x) − m( x1 )

(3.1.2)

ср.

x2 − x1

Запишем формулу (3.1.2) на языке приращений:

		ρср =	m				(3.1.3)
		ρср =	x				(3.1.3)
			x
3. В нашей ситуации плотность меняется неравномерно от точки к
точке, поэтому стержень разобьем на элементарные части							( x должно
быть малым) так, чтобы на элементарном участке [xk −1,						xk ] удельная ли-
нейная плотность изменялась практически равномерно						ρср =	m . Тогда
							x
чтобы вычислить удельную плотность точно, необходимо x							устремить к
нулю. Таким образом, плотность в точке x равна
ρ = lim	m = lim		m( x +	x) − m( x)	.		(3.1.4)
ρ = lim	m = lim				.		(3.1.4)
x→0	x	x→0		x

184

Задача 2 (о силе тока). Пусть q(t) – заряд конденсатора в зави-

симости от времени. Определить силу тока I в произвольный момент вре- мени t через сопротивление R.

Решение. Если бы заряд был постоянным, то силу тока вычисляли

бы по формуле I = q , но поскольку заряд является переменной величи- t

ной, то, рассуждая аналогичным образом как в задаче 1 (провести само- стоятельно), придем к формуле

I (t) =		q (t + t ) − q (t )
	lim			(3.1.5)

	t →0		t
Задача 3 (о мгновенной скорости).			Найти скорость v прямоли-

нейно движущейся точки в произвольный момент t, если путь определяет-

ся формулой S = S (t ) .

Решение.		Проведя рассуждения аналогичные задаче 1, получим
		ν		= lim	S (t +	t ) − S (t )		.	(3.1.6)
		ν	мгн.	= lim				.	(3.1.6)
			мгн.	t →0		t
				t →0		t
Определение 3.1.1.			Касательной к кривой в точке М0						называ-
ется предельное положение секущей М0М при условии, что М → М0.
Задача 4 (о касательной). Найти						уравнение касательной, прове-
денной к графику функции			y = f ( x) в точке (x0,				f ( x0 )) .
Известно, что урав-
нение		прямой	y				M
y − y0 = k ( x − x0 ),							M
y − y0 = k ( x − x0 ),					M0	β		y ( x + x) − y ( x ) = y
k = tg a .						β	0		0
k = tg a .
Из	геометрического				α
анализа	чертежа	следует,			α	x

что tgβ =	y	Тогда	при		x0	x0 + x x
что tgβ =	.	Тогда	при			x0 + x x
M → M 0 ,	x
M → M 0 ,		x → 0 ,
Ðb ® Ða ,	tgb ® tg a
k = tg α = lim tgβ = lim					y = lim	y ( x + x) − y ( x)	.	(3.1.7)
k = tg α = lim tgβ = lim					y = lim		.	(3.1.7)
		x	→0	x→0 x x→0		x

185

Вывод:

1.Все пределы (3.1.4 – 3.1.7) имеют одинаковую математическую структуру и являются математическими моделями, которые характеризуют

скорость изменения определенного процесса (зависимой величины) для каждого значения независимой величины: скорость изменения массы, ско-

рость изменения заряда, скорость изменения пути от времени, скорость изменения ординаты кривой.

2.С математической точки зрения все эти пределы одинаковы и от- личаются только обозначениями.

В математике зависимую и независимую величину принято обозна- чать y и x.

Возникает вопрос: как обозначить скорость изменения зависимой в определенном процессе величины, то есть, функции, в зависимости от ар- гумента.

В математике приняты следующие обозначения:

dy – ввел Лейбниц; dx

xɺ – ввел Ньютон; y′ – ввел Лагранж.

3.2. Определение производной функции в точке

Определение 3.2.1. Производной от функции y = f (x) в точке х называется предел отношения приращения функции к приращению аргу- мента, когда последнее стремится к нулю, если этот предел существует,

конечен и не зависит от способа стремления			x	к нулю
	y′ = lim	y .
	x→0	x
Замечание 3.2.1.	В общем случае y′		–	скорость изменения функ-
ции в точке x0 .
Замечание 3.2.2.	Из школьного курса известно, что геометриче-

ский смысл производной состоит в следующем: производная от функции y = f (x) в точке x0 равна тангенсу угла наклона к оси Ох касательной,

проведённой к графику функции в точке ( x0 , f ( x0 )) (угол отклоняется от оси Ох к касательной).

k = y′ = lim	y .
x→0	x

186

Замечание 3.2.3. Механический смысл производной функции в точке состоит в следующем: производная от функции S , где S (t) - путь,

пройденный материальной точкой за время t , есть мгновенная скорость материальной точки в определенный момент времени:

			′	S
		vмгн (t) = S (t) = lim		.
			t →0	t
	Определение 3.2.2.		Функция называется		дифференцируемой в
точке	′	}) ,	если для неё в точке		x0 существует конечная
точке	x0 ( f (x) С{x0	}) ,	если для неё в точке		x0 существует конечная
производная.
	Определение 3.2.3.		Если производная для функции y = f (x) опре-

делена и существует для всех x из интервала (a, b), то говорят, что функ-

ция y = f (x) дифференцируема на интервале (a,b) : ( f (x) С(′a,b) ) .

Определение 3.2.4. Операция нахождения производной называет-

ся дифференцированием.

3.3. Свойства дифференцируемых функций

Теорема 3.3.1. Если f (x) дифференцируема в точке x0 , то ее при-

ращение Dy , соответствующее x0 и Dx , может быть представлено в виде

		Dy = A × Dx + a(Dx) × Dx ,				(3.3.1)
где	′	α ( x) → 0 при Dx ®0.
где	A = f (x0 ) − const ,	α ( x) → 0 при Dx ®0.
		′	следовательно, сущест-
	Доказательство. По условию f ( x)ÎC{x0} ,		следовательно, сущест-
вует конечная производная		f ′(x ) = const , то есть	f ¢( x		) = lim	y = A , но
		0		0		Dx
					x→0	Dx
тогда по теореме о существовании предела функции					y = A + a(Dx). Сле-
				Dx
довательно, Dy = Df ( x) = A × Dx + a(Dx) × Dx , где a(Dx) ® 0 при						x → 0 .
	Теорема 3.3.2. (необходимое условие дифференцируемости). Если
		′			то функция непре-
y = f ( x) дифференцируема в точке x0 ( f ( x)ÎC{x0} ),					то функция непре-

рывна в этой точке ( f (x) C{x0} ).

187

Доказательство.

По условию функция

′

f ( x) ÎC{x0} , следователь-

но, по теореме 3.3.1 Df ( x) = A × Dx + a(Dx) × Dx , где,

A = f

′

a(Dx) ® 0

(x0 ) ,

при

x → 0 .

Вычислим

lim Df ( x) = lim ( A × Dx + a(Dx) × Dx) = 0 . Тогда,

x →0

по определению непрерывности,

f ( x) непрерывна в точке x0 , что и тре-

бовалось доказать.

y =

Замечание. Обратное утверждение, во-

обще говоря, неверно. Возьмем y =| x | . В точ-

ке x0 = 0 функция непрерывна, но касательная

в ней не определена, следовательно, и произ-

водная также не определена.

3.4.

Дифференциал функции

Определение 3.4.1.

Пусть задана функция

y = f ( x) , дифференци-

руемая в некоторой точке

x0 .

Дифференциалом функции

y = f ( x) в

точке x0 , соответствующим приращению

x ,

называется главная часть

приращения функции, линейная относительно

x . Обозначают dy.

′

Выведем формулу для вычисления dy: y ( x) ÎC{x0

}

по теореме 3.3.1

Dy = y′( x ) × Dx + a(Dx) × Dx .

(*)

При

x → 0

оба слагаемых в выражении (*) –

бесконечно малые, но

второе имеет более высокий порядок малости. Выражение y′( x

) × Dx будет

главной

частью

приращения

y . Она

линейна

относительно x

dy = y′

x .Отсюда будем иметь, что дифференциал независимой перемен-

′

. Тогда,

′

ной dx = x

dy = y dx – формула для вычисления дифферен-

циала произвольной функции.

Из (*) следует:

При

x 1,

y ≈ dy .

Когда

x – бесконечно малая величина, то

y dy или

y y′

при

x → 0

y′ –

коэффициент пропорциональности между бесконечно ма-

лым приращением аргумента и бесконечно малым приращением функции.

188

Выясним			геометрический		y
смысл дифференциала.
y – приращение функции в y(x0+ x)								M
точке x0.					∆y				A
y = MB = MA + AB					∆y				y
y = MB = MA + AB							M0	α	dy
		B ×tga = y′( x ) × Dx = dy ,							dy
AB = M					y(x0)
AB = M	0				y(x0)
	0		0						B
где dy – приращение касательной.								x	B
где dy – приращение касательной.								x
На		рисунке проиллюстри-					x0	x0+ x x
рован	геометрический			смысл			x0	x0+ x x
рован	геометрический			смысл
дифференциала.
Дифференциал функции в точке x0 равен приращению ординаты
касательной, проведенной к графику функции в точке x0.
Когда dx –					′	–	бесконечно малое при-
Когда dx –			бесконечно малая, то dy = y dx			–	бесконечно малое при-
ращение ординаты графика функции.
Замечание 3.4.1.				Если m(x) –	масса куска линейно протяженного
неоднородного стержня в точке x, то					′	–	бесконечно малое при-
неоднородного стержня в точке x, то					dm = m dx	–	бесконечно малое при-

ращение массы, когда длина куска стержня изменяется на бесконечно ма- лую величину dx.

Замечание 3.4.2. Если q(t) – заряд конденсатора в произвольный момент времени t, то dq = q′dt – бесконечно малое приращение (измене-

ние) заряда, когда время изменяется на бесконечно малую величину dt. Замечание 3.4.3. Если S(t) – путь в произвольный момент времени

t, то dS = S′dt – бесконечно малое приращение пути, когда время изменя- ется на бесконечно малую величину dt, т.е. dS – путь, который проходит тело, двигаясь с мгновенной скоростью S′(t ) за бесконечно малый проме-

жуток dt.

Замечание 3.4.4. Применение дифференциала на практике осно- вано на следующем соображении: когда не могут определить значение за- висимого параметра для некоторого объекта, то этот объект разбивают на части так, чтобы внутри разбиения зависимый параметр изменялся равно- мерно, тогда приращение параметра заменяют его дифференциалом:

y ≈ dy = y′dx .

Затем суммируют полученные величины по всему объекту. Например, чтобы вычислить путь при переменном движении, внача-

ле разбивают весь путь на бесконечно малые участки и вычисляют dS = S′dt , затем определенным образом суммируют полученные величины по всему объекту.

189

3.5. Правила дифференцирования. Таблица производных

3.5.1. Правила дифференцирования

Теорема 3.5.1. Пусть u ( x) и v ( x) дифференцируемы в x0 , тогда

вточке x0 имеют место равенства:

1.(u ± v)¢ = u¢ ± v¢ ;

2.(u × v)¢ = u¢v + v¢u ;

Докажем свойство 2. Пусть y = uv . Найдем

	Dy = (u + Du )(v + Dv) - uv = uv + vDu + uDv + DuDv - uv
				Dy = uDv + vDu + Du × Dv
Разделим полученное равенство на Dx						и перейдем к пределу при
Dx ® 0 . Будем иметь
y¢ = lim		y =	lim u ×	v + lim v ×	u + lim	u Dv = uv¢ + vu¢ + u¢ lim Dv =
x→0	Dx		x→0	Dx x→0	Dx x→0	Dx		x→0
=	v	- дифференцируема по теореме 3.2.2					′	′
	v	- дифференцируема по теореме 3.2.2

	v	- непрерывна lim Dv = 0					= v u + u v .
				x →0

Замечание 3.5.1. Аналогичная теорема справедлива и для диффе- ренциалов:

1)d (u ± v) = du ± dv ;

2)d (cu ) = cdu ;

3)d (uv) = udv + vdu ;

190

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 3619 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб40умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб49умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб33умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб38умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб40умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб39умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб39умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб76умк_Яско_ Диф.уравнения_Ряды.pdf