Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Элементы линейной алгебры

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

5.38 Mб

Скачать

☆

<<< < Предыдущая 10 11 12 13 14 15 16 17 18 19 20 2122 / 3622 23 24 25 26 27 28 29 30 31 32 33 34 > Следующая >>>

40. Приведем пример, когда правило Лопиталя применять нельзя, т.к.

	f ′( x)
не существует	lim g ( x)	и нужно обращаться к другим правилам раскры-

тия неопределенностей. Если формально применить правило Лопиталя, то получим

	x2		+ sin x		∞		2x + cos x	2	− sin x
lim				=		= lim		= lim		.
			− sin x
x →∞ x		2			∞	x →∞ 2x − cos x		x →∞ 2	+ sin x

Но предел функции sin x при x → ∞ не существует и, значит, не су- ществует предел отношения производных рассматриваемых функций. По- этому применять правило Лопиталя нельзя. Воспользуемся общим прави-

∞

лом раскрытия неопределенности ∞

	x2	+ sin x		∞	1 + sin x
	x2	+ sin x		∞			x	2
lim			=		= lim		x		= 1.
lim		− sin x	=		= lim		sin x		= 1.
x→∞ x2		− sin x		∞	x→∞	−	sin x
					1
					1		x	2
							x	2

3.15. Исследование поведения функции

При исследовании функциональной зависимости необходимо выяс- нить её особенности, важные свойства. Кроме того, полезно иметь её гео- метрическую иллюстрацию в виде графика заданной функции. Если функ- ция задана аналитически, то её можно успешно исследовать с помощью средств математического анализа: пределов и производной.

I. Возрастание и убывание функции

Теорема 3.15.1. (критерий убывания и возрастания функции).

Дифференцируемая функция y = f (x)

на промежутке (a,b)

возрастает

(убывает)

тогда и только тогда,

когда

f ′(x) > 0 ( f ′(x) < 0)

для любого

x (a,b).

If f ( x) C(′a,b) и f (x) − (↓) f ′(x) > 0 ( f ′(x) < 0) x (a,b).

Пример: Исследовать поведение функции y = x +

на интервале (1, 2).

′

= 1 −

, x (1, 2) имеем 1 −

> 0

у – возрастает на интервале (1, 2).

211

II. Локальный экстремум

Определение 3.15.1. Точки, в которых f ′(x) = 0 или не существует, назовем критическими точками I рода.

Теорема 3.15.2. (первое достаточное условие экстремума). Пусть функция y = f (x) определена и дифференцируема в окрестности точки x0

и x0 – критическая точка первого рода. Тогда, если при переходе через точку x0 первая производная меняет знак, то в точке x0 имеется локаль-

ный экстремум, причем,

−если f ′(x) меняет знак с «–» на «+», то имеется локальный минимум,

−если f ′(x) меняет знак с «+» на «–», то имеется локальный максимум.

′	меняет знак с плюса на минус и x0	–
Доказательство. Пусть f (x)
критическая точка первого рода.
1. Рассмотрим x ( x0 − δ; x0 ) . Функция f ( x) , по условию, диффе-

ренцируема в окрестности точки x0 .					Кроме того, в левосторонней окрест-
ности	точки	x f ′( x) > 0 ,		x − x	< 0 . Тогда по	теореме Лагранжа
		0		0
x ( x0 − δ; x0 )		имеем	c1	( x0 − δ; x0 ) , что
		f (x) − f (x0 ) = f ′(c1)( x − x0 ) < 0 ,
где x0 − δ < c1 < x0 , следовательно, для x ( x0 − δ; x0 )						f (x) < f (x0 ) .
2.	Рассмотрим x ( x0 ; x0			+ δ) . Функция f ( x) , по условию, диффе-

ренцируема в окрестности точки x0 . Кроме того, в правосторонней окрест-

ности точки x		f ′( x) < 0 ,	x − x > 0 .	Тогда по теореме Лагранжа
	0		0
x ( x0 ; x0 + δ)		имеем: c2 ( x0 ; x0 + δ) , что
		f (x) − f (x0 ) = f ′(c2 )( x − x0 ) < 0 ,
где	x0 < c2 < x0 + δ , следовательно, для			x ( x0 ; x0 + δ)	f (x) < f (x0 ) .
	Таким образом, в окрестности точки x0 все значения функции мень-
ше	f (x0 ) , значит, точка x0 –		точка локального минимума, что и требова-
лось доказать.
	Теорема 3.15.3. (второе достаточное условие экстремума). Пусть
x0 –	критическая точка первого рода, и пусть функция				y = f (x) дважды

					′′
дифференцируема в точке x0 ( f (x) C{x0} ), тогда:
−	if	f	′′	–	точка локального максимума;
			(x0 ) < 0 , то x0
−	if	f	′′	–	точка локального минимума.
			(x0 ) > 0 , то x0
					212

Теорема 3.15.4. (третье достаточное условие экстремума).

Пусть x

–

критическая точка первого рода,

f (x) C(n)

{x0}

′

′′

(n−1)

(x0 ) = 0 , а

(n)

(x0 ) ¹ 0 ,

тогда,

если n –

(x0 ) = f (x0 ) = ... = f

нечётно, то в точке x0 экстремума нет, если

n –

чётно,

то x0 –

точка экс-

тремума, причем:

−

(2k ) (x

) < 0 , то x

–

локальный максимум;

−

(2k ) (x

) > 0 , то x

–

локальный минимум.

Замечание. Критерий возрастания и убывания функции, необходи- мое (теорема Ферма) и достаточные условия существования экстремума позволяют исследовать функцию на монотонность и находить точки экс- тремума.

Схема исследования функции на монотонность:

1.Найти D(y).

2.Найти критические точки I рода.

3.Нанести эти точки на числовую прямую с учетом D(y).

4.Исследовать знак y′ внутри полученных промежутков.

5.Сделать выводы.

III. Выпуклость, (вогнутость) функции. Точки перегиба

Определение 3.15.2. Говорят, что функция y = f (x) на некотором промежутке обращена выпуклостью вверх (вниз), если любая хорда, соеди-

няющая точки графика, лежит ниже (выше) графика.

Теорема 3.15.5. (Достаточное условие выпуклости функции).

Пусть y = f (x) имеет вторую производную на некотором промежутке. Тогда:

−если на промежутке f ′′(x) < 0 , то функция обращена выпуклостью

вверх;

−если на промежутке f ′′(x) > 0 , то функция на этом промежутке

обращена выпуклостью вниз.

Определение 3.15.3. Точка, в которой функция меняет направление выпуклости, называется точкой перегиба.

Теорема 3.15.6. (Необходимое условие наличия точки перегиба).

Пусть функция y = f (x) определена в окрестности точки x0 и дважды диф-

ференцируема в точке x0 . Тогда, если x0 – точка перегиба, то f ′′(x0 ) = 0 .

213

Замечание.	Обратная теорема неверна. Приведем пример: y = x4 .
y	y′( x) = 4x3 ;
y = x4	y′′ = 12x2
x	y′′(0) = 0 , точка x = 0 не является точкой перегиба.
x

Определение 3.15.4. Точки, в которых f ′′( x) = 0 или не существу-

ет, будем называть критическими точками II рода.

Теорема 3.15.7. (Достаточное условие наличия точки перегиба).

Пусть функция y = f (x) определена в окрестности точки x0 , дважды диф-

ференцируема в точке x0 , и пусть x0 –	ее критическая точка II рода. То-
гда, если при переходе через точку x	f ′′( x)	меняет знак, то x – точка
0		0

перегиба.

IV. Асимптоты

Построение графика значительно облегчается, если известны его

асимптоты.

Определение 3.15.5. Прямолинейной асимптотой для графика функции y = f (x) называется прямая, расстояние до которой от точки, ле-

y y=kx + b

y = f(x)

жащей на кривой, стремится к нулю при неогра- ниченном удалении от начала координат этой точки по кривой.

Различают следующие виды асимптот:

−вертикальные,

−горизонтальные,

−наклонные.

Теорема 3.15.8.	Если x = a –	точка разрыва второго рода для гра-
фика функции f (x) ,	то прямая x = a – вертикальная асимптота, парал-
лельная оси OY.
Теорема 3.15.9.	Если существуют конечные пределы		lim f (x) = k1
и lim f (x) = k2 , то прямые y = k1 и		x→+∞
		y = k2 – горизонтальные асимптоты,
x→−∞
параллельные оси OX.
Определение 3.15.6. Прямая		y = kx + b называется	наклонной

асимптотой графика функции y = f ( x) , если функция представима в виде f ( x) = kx + b + α ( x),

214

где

lim α ( x) = 0 .	(3.15.1)
x →∞
Теорема 3.15.10. График функции y = f (x)	имеет при x → ∞ на-

клонную асимптоту y = kx + b тогда и только тогда, когда существуют два конечных предела

lim	f ( x)	= k ,	lim	f ( x) − kx = b	(3.15.2)

x→∞	x		x→∞

Доказательство.

Необходимость. Пусть график функции y = f (x)

имеет асимптоту,

определяемую

уравнением

y = kx + b .

Тогда f ( x) = kx + b + α ( x), где

lim α ( x) = 0 .

x→∞

(

)

(

)

(

)

kx + b + α

Значит,

lim

= lim

= lim k +

= k ;

x→∞

lim f ( x)

− kx = lim [b + α(х)] = b .

→∞

x →∞

Таким образом, существуют предельные значения (3.15.2). Достаточность. Пусть существуют предельные значения (3.15.2).

Второе из них означает, что разность f ( x) − kx − b				является бесконечно

малой при x → ∞ . Обозначим эту разность через α ( x) , тогда получим
f ( x) − kx − b = α ( x) или f ( x) = kx + b + α ( x), где lim α ( x) = 0 .
				x→∞
Следовательно,	функция	y = f ( x)	представима		в виде
f ( x) = kx + b + α ( x),	где lim α ( x) = 0 и прямая		y = kx + b является асим-
	x→∞
птотой графика этой функции.
Упражнение.	Определить	асимптоты		графика	функции
y = arctg x − x .

V.Общая схема исследования функции:

1.Найти область определения функции D(y).

2.Найти множество значений функции E(y) (если это возможно).

3.Выделить особенности функции (четность, нечетность, перио-

дичность). Если функция четная или нечетная, то исследование можно проводить только для x ³ 0 . Если функция периодическая, исследование

проводится на основном периоде.

215

4.Исследовать поведение функции на концах интервалов из области определения с помощью пределов. Сделать выводы о непрерывности функ- ции, характере точек разрыва, вертикальных и горизонтальных асимптотах.

5.Найти промежутки монотонности, точки экстремума.

6.Найти промежутки выпуклости, вогнутости и точки перегиба.

7.Найти наклонные асимптоты.

8.Определить точки пересечения графика с осями координат, для этого положить:

−x = 0 - найдем точки пересечения с осью ординат;

−y = 0 - найдем точки пересечения с осью абсцисс.

9.Если есть необходимость, можно составить таблицу дополни- тельных точек.

10.Построить график.

Пример 1: y = 1 + 4x2 (трезубец Ньютона). x

1)D ( y ) = (-¥,0) (0, +¥) .

2)E ( y ) = (-¥, +¥).

3) D(y)

–

симметрична

относительно

начала

координат;

y (-x) = -

+ 4x2

¹ y

( x),

Значит, задана функция общего вида.

¹ - y ( x).

4) lim

+ 4x2

= +¥ ,

lim

+ 4x2

= +¥

горизонтальных

→−∞ x

x→+∞ x

асимптот нет;

lim

+ 4x2

= -¥

, lim

4x2

= +¥

x = 0 –

вертикальная

x→−0

x→+0

асимптота.

5) y¢ = -

+ 8x =

8x3 -1

y′ = 0

при

8x3 -1 = 0 ,

x1 =

y′ –

не существует при x2 = 0 .

y′

216

ymin

= y

= 2

= 3,

x Î(-¥,0)

при

–

y(x)

при x Î

+¥ –

y(x) -

6) y¢¢ = +

+ 8 =

8x3 + 2

y′′ = 0

при 8x3 + 2 = 0 , x1 = -

» -0,62

y′′ не существует при x2 = 0 .

y′′

−

∩

3 2

= -3 4

3 4 = 0 ;

yперег.

= y

+ 4 ×

7) k = lim

= ±¥ наклонных асимптот нет.

lim

x→±∞ x

→±∞

8) при y = 0	1	+ 4x2 = 0 ,	4x3 = -1, x = -3	1	,

	x		4

x ¹ 0 точки пересечения с Oy нет.

-1 − 1	3 2 0	1	x
2

217

Пример 2. y ( x) = ( x -1) e3x+1 . 1) D ( y ) = (−∞, +∞) .

D(y)

–

симметрична

относительно

начала

координат;

y (-x) = (-x -1) e−3x+1 = -( x +1) e−3x+1

¹ y

( x) ,

Значит, задана функция

¹ -y ( x).

общего вида.

lim

y ( x) = lim

( x -1)e3x+1

= ((-¥) × e-¥ ) = (-¥ × 0) =

x®-¥

x -1

lim

= lim

= 0 .

-3x-1

×(- )

-¥

x®-¥

Значит, у = 0 –

является горизонтальной асимптотой функции при х ® – ¥.

lim ( x -1)e3x+1 = +¥ при х ® + ¥ горизонтальных асимптот нет.

x®+¥

4) Исследуем функцию на монотонность

y¢ = ( x -1)¢ e3x+1 + ( x -1)(e3x+1 )¢ = e3x+1 + ( x -1)e3x+1 ×3 = e3x+1 (3x - 2) ;

y′ = 0

при (3x - 2) × e3x+1 = 0 ,

3x − 2 = 0 ,

x =

e3x+1 ¹ 0 .

y′

3×

× e3 .

ymin = y

-1 e

= -

5) Исследуем функцию на выпуклость (вогнутость)

y¢¢ = (3x - 2)¢ e3x+1 + (3x - 2)(e3x+1 )¢ = 3 × e3x+1 + (3x - 2)e3x+1 ×3 = (9x - 3)e3x+1 .

y′′ = 0 ,

9x − 3 = 0 , x =

y′′

3×

e2 .

yперег.

= y

-1 e

= -

∩

Наклонных асимптот при х® −∞ нет, т.к. на −∞ уже имеется го-

ризонтальная асимптота. Определим наклонную асимптоту при х ® + ∞ . Она имеет вид y = kx + b ;

218

k = lim

= lim

( x -1)e3x+1

x→+∞ x

x→+∞

= lim

e3x−1 + ( x -1) × e3x+1 ×3

= lim

(3x

- 2)e3x−1 = +¥ .

x→+∞

Следовательно, наклонных асимптот нет и при x → +∞ .

Точки пересечения графика:

x −1 = 0,

с осью ОХ:

y = 0 ;

( x -1)e3x+1 = 0 ;

¹ 0 ;

e3x+1

А(1, 0) – точка пересечения с осью ОХ;

x =1

с осью ОУ:

x = 0 ;

y = −e .

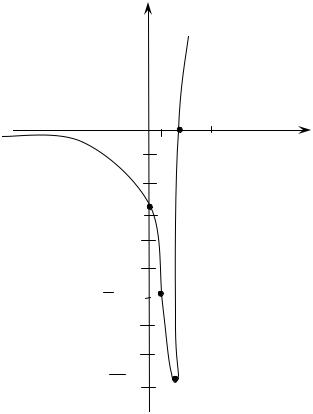
Построим график функции.

0	1	x
-1	1

−e

− 2 e2 3

−e3

3.16.Глобальный экстремум функции

Определение 3.16.1. Наибольшее (наименьшее) значение функции на некотором промежутке называется глобальным максимумом (глобаль-

ным минимумом) или глобальным экстремумом.

Замечание. По свойству непрерывности функция, непрерывная на отрезке [a, b], достигает на нем своего наибольшего (наименьшего) значе-

219

ния. Если точка x0 лежит внутри отрезка, то в точке x0 функция имеет ло-

кальный экстремум и, следовательно, x0 – критическая точка I рода. Таким образом, функция достигает своего наибольшего (наименьшего) значения или в критических точках, или в одном из концов отрезка.

Обозначения:	yнаиб.	yнаим.
	max	min
	P	P

Пример. Найти наибольшее и наименьшее значения функции y = x4 + x3 − x2 на [–1, 2].

1)Находим критические точки I рода. y′ = x3 + x2 − 2x ,

x3 + x2 − 2x = 0 ,
																x = 0 ,									x2 + x − 2 = 0 ,
															1										x2 = −2 [−1, 2] ,
-1	0	1		2					x																x2 = −2 [−1, 2] ,
-1	0	1		2																					x3 = 1.
																									x3 = 1.
2) y (−1) =						1	−		1	−1 =				3 − 4 −12					= −			13		,
2) y (−1) =							−			−1 =									= −					,
					4			3							12		12
y (0) = 0 ,						y (1) =						1	+		1	−1 = −		5		, y (2) =							16	+	8	− 4 =			8		.
y (0) = 0 ,						y (1) =							+			−1 = −				, y (2) =								+		− 4 =					.
											4				3		12									4		3			3
Таким образом,											yнаим.				= y (−1) = −						13		,			yнаиб. = y (2) =						8		.
Таким образом,											yнаим.				= y (−1) = −								,			yнаиб. = y (2) =								.
																	12														3
								3.17. Приложения производной
								к задачам геометрии и физики
Задача 1.						Составить уравнение касательной,																									проведенной к гра-
фику y = y ( x)				в точке ( x0 , y ( x0 )).
Известно,						что					уравнение								прямой,							проходящей через точку
( x0 , y ( x0 )), имеет вид
																y − y0 = k ( x − x0 ),															(*)
т.к. из геометрического смысла производной																										k = y′( x					) , то
																												0
y − y		0	= y′		( x			)( x − x )							– уравнение касательной к кривой y = y ( x)
		0			0						0
в точке	( x0 , y ( x0 )).
																	220

<<< < Предыдущая 10 11 12 13 14 15 16 17 18 19 20 2122 / 3622 23 24 25 26 27 28 29 30 31 32 33 34 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб40умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб49умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб33умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб38умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб40умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб39умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб39умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб76умк_Яско_ Диф.уравнения_Ряды.pdf