Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Элементы линейной алгебры

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

5.38 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 3611 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Введем понятие обратной функции.

Определение 2.5.9.		Пусть	дана
функция y = f ( x)	такая,	что "x Î D ( f ) со-
ответствует одно	и только одно		значение

y Î E ( f ) , т.е., если x1 ¹ x2, то и y1 ¹ y2, где

y1 = f ( x1 ) , y2 = f ( x2 ) . Тогда можно уста- новить обратное соответствие, т.е. считать, что " y Î E ( f ) соответствует одно и только

одно x Î D ( f ) , для которого f ( x) = y .

y = x3

y = 3 x

Очевидно, последнее соответствие будет удовлетворять определе- нию функции, поэтому х есть функция переменной у: x = j( y ) . Обла- стью определения новой функции является E(f ) функции f(x), а областью значений – область определения D(f ). Функцию j(у) называют обратной функцией по отношению к функции f (x).

Понятие обратной функции взаимное, сами же функции f(x) и j(у)

называются взаимно обратными.

Замечание 2.5.1. Любая строго монотонная функция имеет обратную. Для удобства при рассмотрении обратной функции часто переходят к

обычным обозначениям (аргумент х, функция у).

Если при обычных общепринятых обозначениях обратной для функ- ции f(x) является функция j(х), то для получения графика функции y = f ( x) следует повернуть плоскость Оху вокруг биссектрисы первого и

третьего	координатных углов на 180°. Очевидно, что если функция
y = f ( x)	возрастающая (убывающая), то и обратная функция также воз-

растающая (убывающая).

Графики взаимно обратных функций симметричны относительно биссектрисы I и III координатных четвертей.

2.6.Класс элементарных функций

Основные элементарные функции подробно изучались в школьном курсе математики. Поэтому напомним кратко их аналитические выраже- ния и графики.

Определение 2.6.1.	Основными элементарными функциями на-
зываются:
1) y = x p , p	– степенная функция;

101

2)	y = ax , 0 < a ¹ 1 –	показательная функция;
3)	y = loga x , 0 < a ¹ 1	– логарифмическая функция;

4)y = sin x

5)y = cos x

6) y = tg x

– тригонометрические функции;

7)y = ctg x

8)y = arcsin x

9)y = arccos x

10) y = arctg x

–

обратные тригонометрические функции.

11) y = arcctg x

ГРАФИКИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ

1. Степенная функция

y = x p ,

p = const

y=x

y = x2

y = x

y =

y = x 3

y = x

y =

y = 3

1 x

2. Показательная функция			3. Логарифмическая функция
	y = ax			y = loga x

	y			y	y = loga x,
y = ax ,		y = ax ,			(a > 1)
(0 < a < 1) 1		(a > 1)	0			x
			0			x
0		x			y = loga x,
0		x			(0 < a < 1)
					(0 < a < 1)

102

4.Основные тригонометрические функции:

		y = sin x				y = cos x
			y			1	y
		1				1
	− π	1	3 π	− 3	π			3 π
	− π		3 π	− 3	π		π	3 π
	2		π 2	2	– π	− π	π	2
− 3 π	–- π 0		π	x		− π	π	x
2		–1	2			2	2
		–1					– 1

												y = ctg x
				y = tg x								y = ctg x
				y = tg x


				y									y
				0 − π	π	3	π					− π			3	π
						3									3
					2	2									2
			– π	2	2	2					2				2
−	3	π	– π	0	π		x	−	3	π	– π 0		π	π		x
	2								3				2

								2

5.Обратные тригонометрические функции:

y = arcsin x

y = arctg x

y = arccos x

− π

y = arcctg x

–1

−

–1 0

103

Определение 2.6.2. Элементарной называется функция, которая может быть получена из основных элементарных функций с помощью ко- нечного числа алгебраических операций или образования сложных функ- ций, причем аналитическое представление функции должно содержать од- ну формулу.

Например,

y =	cos2	x - log5	x - 3 x4
				–	элементарная функция,
		x tg7
			x
y =1 + x + x2 + ... + xn + ... –					неэлементарная функция,
	0,	если x < -2
y =					неэлементарная функция.
	2 + 3x, - 2 £ x < 4 –
		x ³ 4
	x5 ,

Среди элементарных отдельный интерес представляют так называе-

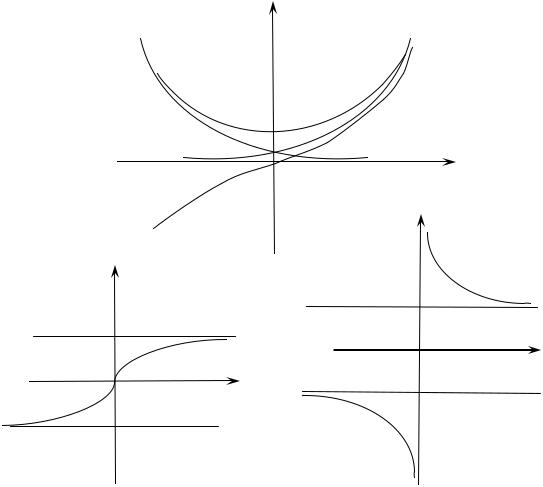
мые «гиперболические функции».
Определение 2.6.3.	Гиперболическим синусом называется функ-
ция, определяемая формулой sh x =		ex - e− x
				.
		2		.
		2
Определение 2.6.4.	Гиперболическим				косинусом называется
функция, определяемая формулой ch x =			ex + e− x		.
функция, определяемая формулой ch x =			2		.
			2
Определение 2.6.5.	Гиперболические тангенс и котангенс функ-

ции определяются соответственно формулами: th x = sh x , c th x = ch x .

		ch x	sh x
Замечание 2.6.1.	Очевидно, что гиперболические функции имеют
определенные значения	при всех	x , за исключением	функции
y = c th x , которая не определена при		x = 0 .
Замечание 2.6.2.	sh 0 = 0, ch 0 =1, ch2 x - sh2 x =1.

Замечание 2.6.3. Гиперболические функции напоминают триго- нометрические, однако не обладают важнейшим свойством тригонометри- ческих функций – периодичностью.

104

ch x

		0	x
	sh x
		y
			cht x
y		1
		1
1
	th x	0	x
		0	x
0	x	–1
	x

–1

2.7.	Числовая последовательность.
Предел числовой последовательности
Определение 2.7.1. Числовой последовательностью называется
функция от натурального аргумента (числа)
	xn = f (n) .	(2.7.1)
Выражение xn	называется общим членом последовательности. Чи-
словую последовательность принято обозначать { xn}n N .
Из определения следует, что числовая последовательность –		бесчис-
ленное множество действительных чисел.

Приведем примеры некоторых числовых последовательностей:

10. 1, 2, 3, 4, …,	{ n}
20 . 1 , 4, 9, …	{n2}

105

30 1; 1 ; 1 ; ...

2 3

40. xn = (−1)n

50. xn = 12 n

60. xn = a1 + d (n −1) 70. bn = b1qn−1

Определение 2.7. 2.

–1, +1, –1, …

1, 1 , 1 , ...

–арифметическая последовательность,

–геометрическая последовательность.

Выражение для xn называется общим членом

последовательности.

Любой член последовательности может быть получен из общего подстановкой в (2.7.1) соответствующего номера члена. Например,

x =	2n −1	,	x =	9
	5n + 3
n			5	28

Числовую последовательность принято обозначать точками число-
вой прямой.
Определение 2.7.3. Число а			называется пределом числовой по-

следовательности {xn }n N , если для любого, сколь угодно малого, ε > 0 существует такой номер Nε , начиная с которого для всех n > Nε вы- полняется неравенство

xn − a		< ε	(2.7.2)

или

ε > 0 Nε , n > Nε xn − a < ε .

Обозначается lim xn = a .
n→∞
Неравенство (2.7.2), как известно, эквивалентно неравенству
a − ε < xn < a + ε	(2.7.3)

Число а характеризует поведение большинства членов последова- тельности, т.е. показывает, что с увеличением номера в процессе, когда n→∞, члены последовательности находятся вблизи а.

Из определения следует, что для любого ε > 0 можно указать такой номер, начиная с которого все члены последовательности попадают в ок- рестность точки а.

106

Определение 2.7.4. Говорят, что последовательность { xn }n N в

процессе при n → ∞ имеет бесконечный предел, если для любого, доста-

точно большого, M > 0	существует такой номер			NM ,	что n > NM
выполняется неравенство		xn	> M . Обозначается	lim xn = ∞ .
выполняется неравенство		xn	> M . Обозначается	lim xn = ∞ .
				n→∞
				n→∞
Определение 2.7.5.		Если последовательность {xn }n N			имеет конеч-

ный предел, то ее называют сходящейся, если же предел равен бесконечно- сти или не существует, то последовательность называют расходящейся.

Теорема 2.7.1. Если предел числовой последовательности сущест- вует, то он единственный.

Замечание 2.7.1. Последовательность {xn } можно рассматривать

как функцию натурального аргумента, поэтому все свойства функции имеют место и для последовательности. Последовательности могут быть

возрастающими и убывающими, ограниченными и неограниченными.

Теорема 2.7.2. (достаточное условие сходимости числовой последо-

вательности). Если последовательность {xn }n N монотонно возрастаю-

щая (убывающая) и ограничена сверху (снизу), то она имеет конечный предел.

2.8. Бесконечно малые и бесконечно большие числовые последовательности. Свойства бесконечно малых

и бесконечно больших числовых последовательностей

Бесконечно малые величины – очень важный класс переменных ве- личин, играющих первостепенную роль в высшей математике.

Определение 2.8.1.	Числовая последовательность {xn } называется
бесконечно малой числовой последовательностью,			если	lim xn = 0
				n→∞
для ε > 0 Nε такой,	что n > Nε следует	xn	< ε .
для ε > 0 Nε такой,	что n > Nε следует	xn	< ε .
Определение 2.8.2.	Числовая последовательность {xn } называется
бесконечно большой, если	lim xn = ∞ М > 0 NM ,			n >NM	сле-
	n→∞

дует xn > M .

107

Теорема 2.8.1. Если { xn } бесконечно малая числовая последова-

		1
тельность, то			–	бесконечно большая числовая последовательность и

		xn
наоборот, если {xn } –				бесконечно большая числовая последовательность,
1
то	–	бесконечно малая числовая последовательность.

xn

Замечание.2.8.1. Условно данное утверждение записывается так

1		= 0 ,	(2.8.1)


∞
1
	= ±∞ .		(2.8.2)
0

При этом будем понимать:

− выражение (2.8.1) означает, что, если в равенстве 1 = α величина x

х безгранично возрастает, то величина α в том же процессе безгранично приближается к нулю;

− выражение (2.8.2), например, для равенства tg π = +∞ означает, 2

что в процессе, когда ϕ неограниченно приближается к π слева, величина

tg ϕ безгранично растет.

Замечание 2.8.2. Нужно различать практические бесконечно ма- лые и бесконечно большие величины от математических бесконечно ма- лых и бесконечно больших величин. Так, в процессе безграничного рас- ширения газа данной массы плотность и давление будут величинами бес- конечно малыми. Но безгранично газ в реальной действительности расши- ряться не может. Это могут предполагать синоптики, экологи и т.п.

Практическая бесконечно малая величина – это переменная или по- стоянная величина, достаточно малая по сравнению с участвующими ко- нечными величинами (плотность в сравнении с объемом) настолько малая, чтобы можно было без существенной ошибки применять по отношению к ней свойства «математических» бесконечно малых величин.

108

Свойства бесконечно малых числовых последовательностей

(без доказательства)

1.Алгебраическая сумма (±) бесконечно малых числовых последо- вательностей есть бесконечно малая числовая последовательность.

2.Произведение ограниченной числовой последовательности на бесконечно малую числовую последовательность есть бесконечно малая числовая последовательность. (Следовательно, произведение двух беско- нечно малых числовых последовательностей – бесконечно малая числовая последовательность).

Замечание 2.8.3. Если в ходе некоторого процесса число слагае- мых бесконечно малых величин неограниченно растет, сумма их, вообще говоря, может и не быть бесконечно малой величиной.

(

+ ... +

→ 0 ,

+ ... +

→ ∞ ).

Свойства бесконечно больших числовых последовательностей

(без доказательства)

1.Алгебраическая сумма (±) бесконечно больших числовых после- довательностей есть бесконечно большая числовая последовательность.

2.Произведение ограниченной числовой последовательности на бесконечно большую числовую последовательность есть бесконечно боль- шая числовая последовательность.

3.Произведение двух бесконечно больших числовых последова- тельностей есть бесконечно большая числовая последовательность.

Неопределенные выражения

Естественным образом возникает вопрос: что будет, если

б.б. = ∞ 1. ?

б.б. ∞

	б.м.		0
2.		=		?
	б.м.		0

3. б.б. – б.б. = (∞ – ∞)?

Определение 2.8.3. Выражения	∞	,	0	,	(∞ − ∞) называются не-


	∞		0

определенными. Неопределенными будут также выражения (1∞ ), (00 ) и т.п.

109

Название связано с тем, что в результате раскрытия этих неопреде- ленностей могут быть получены различные результаты (конечные или бес- конечные пределы и т.п.).

Правило 2.8.1. (раскрытия неопределенности ∞ ). При раскрытии

∞

неопределенности вида ∞ можно числитель и знаменатель дроби разде-

∞

лить на величину, имеющую в данном процессе наибольший порядок не- ограниченного роста (бесконечности).

Например,

		7n3	+ 8n2	- 9	¥			7 +		8	-		9
																7
										n			n	3		7
1.	lim				=		= lim						n		=		= ¥ .
1.	lim				=	¥	= lim	3			2				=		= ¥ .
	n→∞ 3n2 - 2					¥	n→∞	3			2					0
										-
									n	-		n3

(n +1)!

(n + 2)!

(n +1)!+ (n + 2)!

(n + 3)!

2. lim

= lim

(n + 3)!

(

) + (

)

n→∞

! n→∞ (n + 2)!

(n + 3)!

(n + 2)(n + 3)

(n + 3)

= lim

= 0 .

n→∞

(n + 3)

Замечание 2.8.4. В математике принято произведение первых на-

туральных n чисел обозначать как n! . Таким образом,

n! =1× 2 × 3 ×... × n,

(n +1)! = n!(n +1),

(n + 3)! = (n +1)!(n + 2)(n + 3).

По определению 0! = 1.

2.9.

Предел функции

Рассмотрим функцию y = f ( x), задан-

ную на произвольном множестве.

Определение 2.9.1. (по Гейне).

Число

А называется пределом функции

y = f (x) в

х1 х0 х2 х3

процессе при

x → x0 , если для любой чи-

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 3611 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб40умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб49умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб33умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб38умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб40умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб39умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб39умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб76умк_Яско_ Диф.уравнения_Ряды.pdf