
Kluwer - Handbook of Biomedical Image Analysis Vol
.2.pdf372 |
Xu et al. |
generally difficult to obtain ideal segmentation results when they are applied into other types of images. In recent years, some studies have been conducted to take advantages of a few algorithms to improve the segmentation performance, such as the wavelet MRF method [28], the region competition [29], and the Fuzzy Snake [32], etc. In this study, we develop our solutions following this problemsolving approach.
The research on segmentation techniques at an early stage was more on single frame gray level or monochrome images according to the survey provided by Haralick and Shapiro [10]. One category of these algorithms is region-based segmentation that includes region growing, splitting, and merging techniques. They generally use the intensity smoothness or similarity among neighboring pixels to find the regions. Another category of approaches find regions based on the discontinuities or edges in image. Since the closed contour is usually hard to be obtained in the edge map generated by various edge detectors, such as gradient operators or Canny edge operator [15], a tedious and more challenging linking procedure has to be employed to find closed region boundary. Active contour model (ACM)-based algorithms are a category of segmentation methods that search the contour of a particular object by minimizing a curve energy function. Bayesian inference based algorithms are another category of segmentation methods. They usually define the segmentation result image (a label matrix) as a sample of 2-dimensional random field and find the optimal solution by performing maximum a posterior probability (MAP) estimation. The label matrix is usually modeled as Markov random fields (MRF) [21, 22] and computed by means of clique potential functions according to its duality with Gibbs random fields (proved by the Hammersley–Clifford theorem [33]). In recent publications, most of the research works are focused on the accurate model description [20], optimized energy minimization searching algorithms design [19], as well as the performance improvement by introducing new models [28].
The study of image sequences segmentation can be regarded as an extended application area of single frame segmentation approaches. In addition to the segmentation results on each frame of the sequence, the correlation between adjacent frames is often considered, and hence, it makes the automatic/ semiautomatic processing possible. Even though some approaches have been proposed before [34–37], the designs of algorithms are usually decided by the detailed correlated features in applications. In our study on the atherosclerotic
Segmentation Issues in Carotid Artery Atherosclerotic Plaque |
373 |
disease diagnosis, the 2-dimensional cross section images are obtained in a parallel sequence with small distance between each two along human’s carotid artery.
While the study of gray-level image segmentation is still an active area of research, there is a growing need for solutions to partition multiple channel or multiple spectral images. In our study, multiple contrast weighting images on the same subject are used to identify tissue types. The other typical application areas of multiple channel image segmentation technique include remote sensing images, color images, and multiple modality medical images. Similar to the solutions for monochrome images, there also exist algorithms for multiple channel images segmentation based on edge detecting [38, 39], region growing [40, 41], and region splitting and merging [42]. However, they are facing the same problems as in monochrome domain. A new category of methods for multiple channel images is based on the histogram analysis [43] and clustering [44, 45] in multiple dimension data space. Because of the absence of spatial constraints in an image domain, the performances of such methods are often limited due to the existence of strong noises in images. The Bayesian-based approaches have also been proposed [46, 47]. They are basically extended 2-dimensional models to a multiple dimension data space. However, because of the dramatic increase of computation in the practical implementation they cannot be applied to those time-demanding applications, such as image database retrieval. In recent publications, Comaniciu and Meer [48] proposed a method that integrates the spatial constraints and feature domain cluster searching results to improve the segmentation results for color images.
The material in this chapter is organized as follows. Following this introduction, section 8.1 focuses on the segmentation technique for single contrast weighting (gray level) MR image. It covers Bayes’s theorem, MAP estimation, MRF model, and the existing algorithms based on MRF. Finally, the QHCF algorithm is discussed and some experiments are conducted to analyze its performance. Section 8.3 covers the MR image sequence technique and an image segmentation framework, a MRF-based active contour model. It also includes a brief review of the traditional active contour model and its enhanced version, minimal path approach. Section 8.4 is about multiple contrast weighting MR image segmentation solutions. It consists of two parts. The first part describes a multidimensional MRF (mMRF) and its corresponding multidimensional QHCF based solution. The second part is about clustering-based segmentation method.
374 |
Xu et al. |
Section 8.5 introduces the specific segmentation methods that we use in fibrous cap analysis.
8.2MRF-Based Gray-Level Image Segmentation
8.2.1 Introduction
In this section, we will discuss the segmentation techniques for gray-level image. This is because the subjects in our study, the MR images, are gray level intensity based, with pixel intensity within range 212–216 defined by different MR scanner manufactures. In addition, the methods for gray-level image are usually the basis for processing of a MR image sequence and multiple contrast images.
Gray-level image segmentation techniques have been studied for years. Among the existing algorithms in literature, some are based on the pixel intensity distribution or histogram [49–52], some use region-based splitting/merging approaches [11–14], and some are derived from morphological operations [53, 54]. They have been successfully employed in many applications. However, the drawback of these algorithms is the poor performance in noisy environment. Some Bayesian inference based segmentation techniques [19–22, 55], using the MRF as image model to improve robust performance to noise, have been proposed in recent years and become very popular.
This section will focus on the MRF model and its application on gray-level image segmentation. An enhanced version of the Highest Confidence First algorithm is introduced.
8.2.2 Markov Random Field
MRF has become a significant statistical signal modeling technique in image processing and computer vision. Generally speaking, the MRF model assumes that the information contained in a particular location is affected by its neighboring local structure of a given image rather than the whole image. In other words, the estimation of pixel’s properties, such as intensity, texture, color, etc., closely relates to a neighborhood of pixels, and this dependency can be characterized by means of a local conditional probability distribution. This hypothesis can
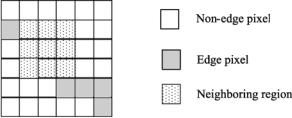
Segmentation Issues in Carotid Artery Atherosclerotic Plaque |
375 |
S
h
g
Figure 8.1: Illustration of MRF neighborhood and edge constraint. s and g are no-edge pixels belonging to different regions and h is an edge pixel within the s neighborhood.
reduce the complexity of the image modeling and provides a convenient and consistent way of describing the observed images.
8.2.2.1 Definition
Assume a two-dimensional random field is with size I by J. For any pixel at location (i, j), 1 ≤ i ≤ I, 1 ≤ j ≤ J, its neighborhood, Ni, j , can be defined as
1.pixel (i, j) / Ni, j and
2.for any pixel ( p, q) Ni, j , there is (i, j) Np,q
To illustrate the neighborhood, an example is shown in Fig. 8.1. The shaded region is a 3 by 3 neighborhood of pixel s. The size of neighborhood generally reflects how far a pixels surrounding region has an affect on it. This is a detail of the implementation of the algorithm and depends on the characteristics of the processed image.
Assume X is a two-dimensional random field and denotes the set of all the possible samples of X. The definition of Markov random field is given as follow:
if X is an MRF, then for every Xi, j X it must satisfy
(i) |
P(Xi, j |X p,q all ( p, q) = (i, j)) = P(Xi, j |X p,q |
all ( p, q) Ni, j ) (8.1.a) |
(ii) |
P(X = x) > 0 for all x O |
(8.1.b) |
Condition (i) is called the Markovian property that describes the statistical dependency of any pixel in the random field on its neighboring pixels. Under this constraint, only a small number of pixels within Xi, j ’s neighborhood, Ni, j , instead of the whole image needs to be considered. Thereby, it reduces the
378 |
|
|
|
|
|
|
|
Xu et al. |
be written as: |
|
|
|
|
− |
|
|
|
P(X |
= |
x) |
= |
Z |
s c Ns |
T |
||
|
|
1 |
exp |
|
VsP(x) + VsE(x) |
(8.9) |
8.2.2.2 Maximum a Posterior Probability
Given an observed image Y, for any pixel at location s in Y, we assume it is with intensity ys and with label xs in segmentation label matrix. Then the a posteriori probability of segmentation result can be expressed as
P(X |
| |
Y) |
= |
P(Y | X) P(X) |
, |
(8.10) |
|
||||||
|
|
P(Y) |
|
|||
where P(Y | X) is the conditional probability of the observed image given the scene segmentation. The goal of maximum a posterior probability (MAP) criterion is to find an optimal estimate of X, Xopt, given the observed image Y. Since P(Y) is not a function of X, the maximization process only applies over the upper portion of Eq. (8.10), P(Y | X) P(X). More accurately, given the observed image, the target of solving an MRF is to find the optimal state Xopt that maximizes the a posterior probability and take that state as the optimal image segmentation solution.
In this study, the conditional density is modeled as a Gaussian process, with mean µs and variance σ 2 for the region that s belongs to in the image domain. Thus, the intensity of each region can be regarded as a signal µs plus additive zero mean Gaussian noise with variance σ 2, and the conditional density can be expressed as
P(Y |
| |
X) |
|
exp |
|
(ys − µs)2 |
. |
(8.11) |
|
||||||||
|
|
|
− s 2σ 2 |
|
||||
By substituting Eqs. (8.9) and (8.11) into (8.10), the general form of the a posterior probability can be written as
P(X | Y) P(Y | X) P(X) |
2σ 2 |
Z |
− s c Ns |
|
T |
|
|||||||
− s |
|
|
|||||||||||
|
exp |
(ys − µs)2 |
|
|
1 exp |
VsP(x) + VsE(x) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
− s |
|
2σ 2 |
|
+ c Ns |
T |
|
(8.12) |
|||||
1 |
exp |
|
(ys − µs)2 |
|
VsP(x) + VsE(x) |
||||||||
|
|
|
|
|
|
|
|
|
|
||||
Segmentation Issues in Carotid Artery Atherosclerotic Plaque |
379 |
Since Z is a constant, therefore, the a posterior probability can be simplified as
P(X |
| |
Y) |
|
|
− s |
|
2σ 2 |
|
|
+ c Ns |
|
|
|
|
|
|
T |
|
|
|
|
|
(8.13) |
|||||||||||||
|
|
|
exp |
|
|
|
(ys − µs)2 |
|
|
|
|
VsP(x) + VsE(x) |
|
|||||||||||||||||||||||
Under MAP criterion, the optimal segmentation result should satisfy |
||||||||||||||||||||||||||||||||||||
Xopt = max arg{P(X | Y)} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
|
X |
|
|
|
|
− s |
|
|
|
2σ 2 |
|
|
+ T c Ns sP |
|
|
+ sE |
|
||||||||||||||||||
|
X |
|
|
|
|
|
|
|
(x) |
|||||||||||||||||||||||||||
|
max arg |
exp |
|
|
|
|
(ys − |
µs)2 |
1 |
|
|
|
(V |
|
|
V |
(x)) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ T c Ns |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
||||||
|
X |
|
s |
|
|
2σ 2 |
|
|
|
|
sP |
(x) |
sE |
(x)) |
(8.14) |
|||||||||||||||||||||
|
min |
arg |
|
|
(ys − µs)2 |
|
|
1 |
|
|
(V |
V |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We define the energy function of an MRF as |
|
+ |
|
|
|
|
|
|
||||||||||||||||||||||||||||
E(X) |
= |
s |
|
|
|
|
2σ 2 |
|
|
+ T c Ns |
|
sP |
(x) |
sE |
|
|
|
(8.15) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Therefore, the optimal segmentation searching is equivalent to the minimization process of the MRF:
Xopt = min arg E(X) |
(8.16) |
X O |
|
8.2.2.3 Energy Minimization Method
The discussion in section 8.2.2.2 shows that in an MRF the optimal segmentation solution comes from finding the maximum of the a posteriori probability in Eq. (8.14), which is equivalent to the minimization problem of the energy function of Eq. (8.16). However, because of the large size of high-dimensional random variable X and the possible existence of local minima, it is fairly difficult to find the global optimal solution. Given the image size with I by J and the gray level for each pixel is Ng, the total size of the random field solution space is NgI×J that usually requires a huge amount of computation to find the optimal solution. For example, the size of MR image on carotid artery is usually 256 by 256, the gray level of each pixel is 212, then the number elements of the solution set is (212)256×256 = 2786432, it is a prohibitive to be implemented in most interactive applications.
Some algorithms have been proposed to solve this problem in literature. Generally speaking, they can be classified into two categories. One category

Segmentation Issues in Carotid Artery Atherosclerotic Plaque |
381 |
Suppose that the temperature parameter is at certain value T and the random field X starts from any arbitrary initial state, X(0). By applying a perturbation randomly, a new realization of the random field can be generated as X(n+1). The implementation of this perturbation varies in different optimization scheme. For example, in Gibber sampler, only one pixel is changed in each scan, while all the other pixels are kept unchanged. Generally speaking, the perturbation is usually very small so that X(n+1) is in the neighborhood of its previous state, X(n). The probability of accepting this perturbation is decided by two factors:
(i)Total energy change, E, due to this perturbation.
(ii)Temperature T .
The definition of acceptance probability is defined as
Paccept = |
e |
E |
if E > 0 |
|
||
T |
(8.17) |
|||||
1− |
|
if E |
≤ |
0 . |
||
|
|
|
|
|
|
|
It is obvious that the perturbations that lower the energy will be definitely accepted. However, when there is an increase of energy, the temperature parameter T controls the accepting probability in that given the same energy change
E, when T is with relative high value, the accepting probability is more than when T is relatively lower. Since this probability is based on the overall energy change, it has no dependency on the scanning sequence as long as all the pixels have been visited. In each iteration, this perturbing-accepting process will go on until the equilibrium is assumed as being approached (this is generally controlled by the maximum times of iteration). Then the temperature parameter T is reduced according to an annealing schedule and the algorithm will repeat the iterations for equilibrium searching as discussed above with the newly reduced temperature.
This annealing process will keep on going until the temperature is below the minimum temperature defined. Then the system is frozen and the state with the lowest energy is reached.
The annealing schedule is usually application-dependent since it is very crucial to the amount of computation in the stochastic relaxation process and the accuracy of the final result. Gemen and Geman proposed a temperature-reducing schedule that is expressed as a function of the iteration numbers:
τ
T = (8.18) ln(k + 1)
