1.2. Виды движения

1.2.1. Равномерное, прямолинейное

Движение называется равномерным и прямолинейным, если точка движется по прямой линии с постоянной скоростью .

Рассмотрим движение материальной точки с постоянной скоростью вдоль оси OX (рис. 1.8). Пусть в начальный момент времени t=0 координата точки х = х₀, а скорость совпадает с направлением движения.

Н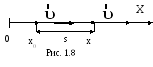айдем координату х и путьs, пройденный точкой за интервал времени t.

За малый интервал dt перемещение точки

,

где – проекция вектора скоростина ось ОХ.

Проинтегрируем левую и правую часть последнего равенства в пределах изменения переменных x и t

,

, (1.19)

.

В случае когда вектор скорости не совпадает с направлением движения

.

При прямолинейном равномерном движении пройденный точкой путь

. (1.20)

1.2.2 Равнопеременное прямолинейное

Движение называется равнопеременным и прямолинейным, если тело перемещается по прямой линии с постоянным ускорением . Равнопеременное прямолинейное движение может быть равноускоренным, когда вектор ускорения совпадает с вектором мгновенной скорости и равнозамедленным, когда ему противоположен (рис. 1.9).

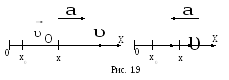
Пусть в начальный момент времени координата точки x=х₀, скорость совпадает с направлением оси ОХ, тогда

при равноускоренном движении , равнозамедленном .

За время t пройденный точкой путь.

, (1.21)

где – модуль проекции вектора скорости на ось OX находится из соотношения интегрированием его левой и правой части в пределах изменения переменных и t

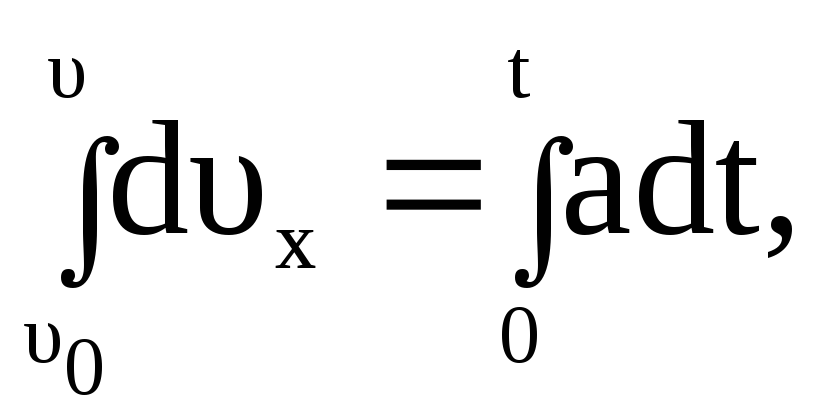
При подстановки в соотношение (1.19) скорости для равноускоренного движения пройденный путь

,

координата точки

. (1.22)

Для равнозамедленного движения проекция скорости и координата точки определяются по формулам

.

. (1.23)

Путь пройденной точкой

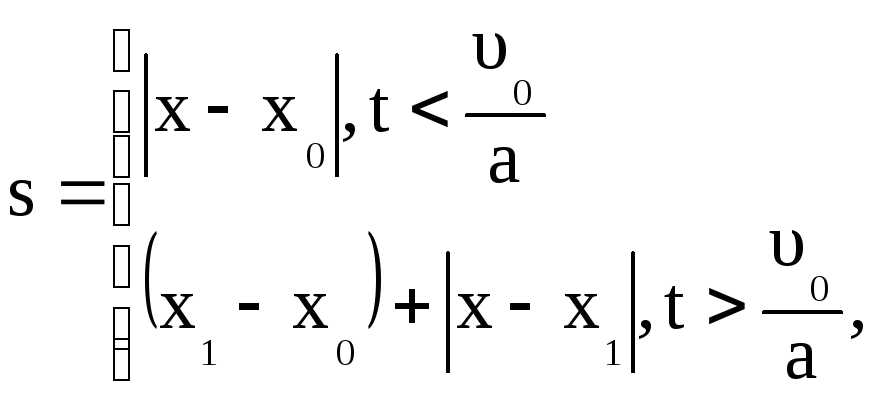
где .

1.2.3 Равнопеременное

Движение называется равнопеременным, если тело перемещается по тра­ек­то­рии с постоянным вектором ускорения.

Примером равнопеременного криволинейного движения является движение тела брошенного со скоростью под углом к горизонту (рис. 1.10) Движение тела происходит в гравитационном поле Земли с постоянным ускорением свободного падения. Для определения положения тела в пространстве разложим его движение на равномерное прямолинейное по оси OX со скоростью и равнопеременное по оси OY с ускорением свободного падения g и начальной скоростью .

Вмомент времени t координаты тела

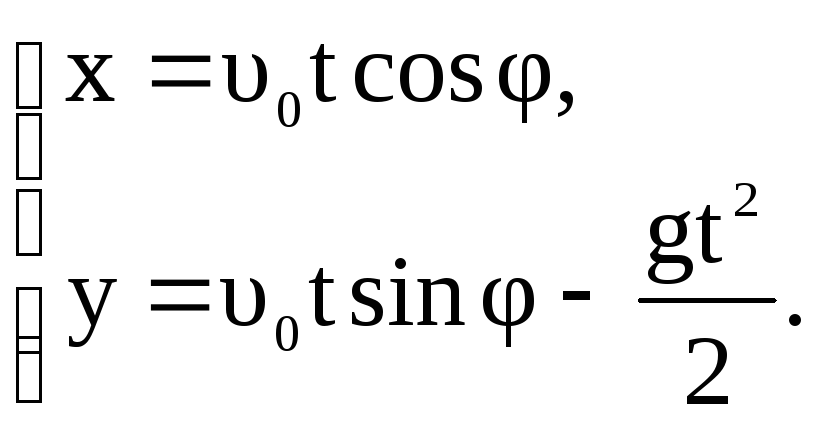(1.25)

вектор скорости

. (1.26)

Модуль вектора скорости

, (1.27)

где .

Уравнение траектории найдём путем исключения параметра t из равенств (1.25)

. (1.28)

Ускорение свободного падения в любой точке траектории можно разложить на его касательную и нормальную составляющие, где модуль касательного ускорения

, (1.29)

где α-угол между векторами скорости и ускоренияg в заданной точке траектории

Модуль нормального ускорения

. (1.30)

Из сравнения уравнения параболы и равенства (1.28) следует, что тело, брошенное под углом к горизонту, движется по параболе.

Задания для самоконтроля знаний.

1. Определить путь пройденный автомобилем за 2 часа его движения со скоростью 90 км/ч.

2. Определить время обгона легковым автомобилем грузовика, если водитель совершает этот маневр при начальной скорости 80 км/ч с ускорением 2 м/с².

3. Определить тормозной путь поезда движущегося со скоростью 36 км/ч при времени торможения 1 минуты.

4. Определить максимальную высоту подъема снаряда имеющего начальную скорость 100м/с и выкатившего из орудия под углом 45° к горизонту.

Лекция 3

1.2.4 Равномерное, вращательное

Рассмотрим движение м.т. по окружности радиусом R с постоянной линейной скоростью вокруг неподвижной осиZ (рис. 1.11).

Положение точки определяет радиус-вектор .За малый интервал времени радиус-вектор повернется на угол. Направление поворота м.т. вокруг осиZ задается вектором и правилом правого винта: поступательное движение правого винта и вектора совпадают, если вращение точки и винта совершается в одинаковом направлении. Модуль вектора равен углу поворота за интервал времени. Линейное перемещение вектораза времяdt

(1.31)

где – угол между вектороми вектором.

Вектор линейной скорости движения точки

, (1.32)

где – вектор угловой скорости.

Вектор угловой скорости совпадает с направлением вектора).

Модуль вектора линейной скорости

. (1.33)

Вектор линейного ускорения

, (1.34)

где – вектор углового ускорения, – вектор касательного ускорения, – вектор нормального ускорения.

Направление вектора углового ускорения совпадает с направлением вектора(), если угловая скорость возрастает, и противоположно () , если она уменьшается.

Модули векторов ,

.

. (1.35)

Угловой путь м.т., движущейся по окружности за время dt

.

Угловой путь точки за интервал времениt при начальном угле

.
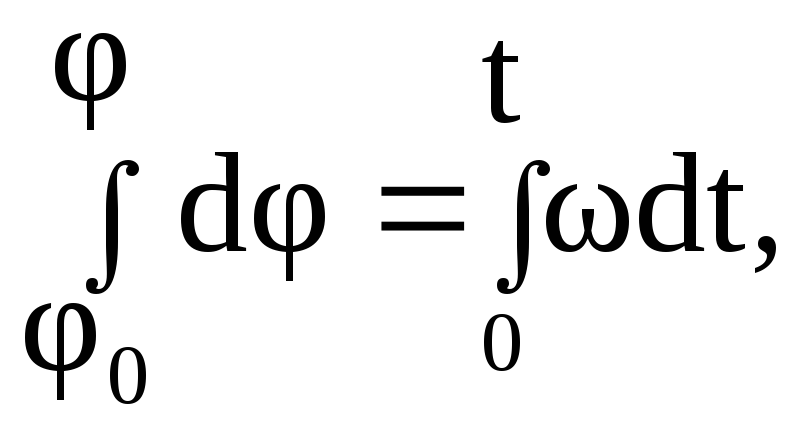