7.6 Давление идеального газа на стенку

Д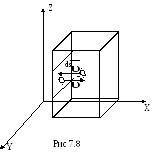авление газа в сосуде определяется взаимодействием его молекул со стенкой. Выделим на поверхности стенки сосуда достаточно малую площадкуdS (рис 7.8), чтобы можно было ее считать кулы, находящиеся в сосуде, движутся в направлении этой площадки с одной и той же скоростью υ. Вдоль оси ОХ движется 1/3 общего числа молекул N и 1/6 N к стенке сосуда.

Тогда о площадку dS, за некоторый промежуток времени dt ударяется число молекул:

где n – концентрация молекул в сосуде. υdtdS – объем слоя из которого молекулы ударяются о стенку.

Каждая молекула будет отскакивать от стенки со скоростью, равной скорости до соударения, но противоположного направления (упругое соударение) и передавать импульс силы

fdt=∆(mυ),

где ∆(mυ)=mυ₂ – mυ₁, ∆(mυ) = mυ – (–mυ) = 2mυ.

Импульс силы, полученный стенкой от молекул, ударяющихся о площадку dS, будет равен

.

Сила действующая на площадку dS стенки сосуда

Давление молекул на стенку

(7.13)

Если учесть, что скорости молекул имеют разные величины и направления, то

(7.14)

где =1/2(mυ²) - средняя кинетическая энергия поступательного движения молекулы.

Так как концентрация молекул, п = N/V, то

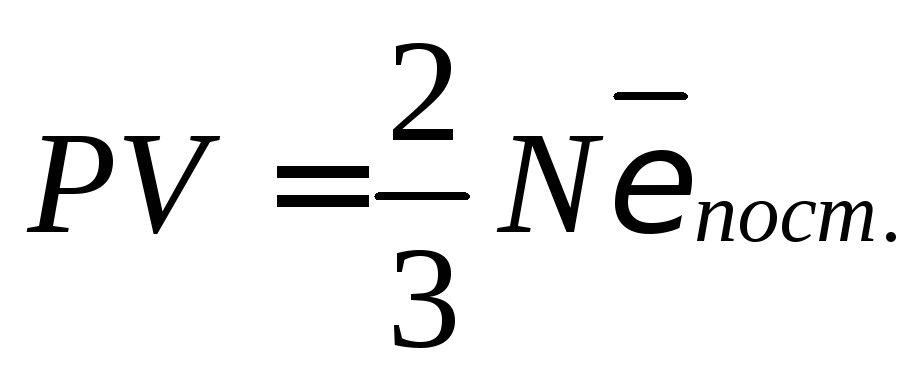, (7.15)

где E_к·Nε_пост.=ε_пост. — суммарная кинетическая энергия поступательного движения всех молекул газа.

7.7 Уравнение состояния идеального газа

Опытным путем было получено отношение, которое равно постоянной велечине.

При условии, что газ имеет Р = 1,01∙10⁵Па,

Т = 273 К, V = 22,4·10^-3 м³/моль (нормальные условия).

.

Полученное значение называется универсальной газовой постоянной и обозначается R. В соответствии с принятым обозначением для одного моля газа

.

Для идеального газа молярной массой μ и массой M

(7.16)

где ν – число молей в газе массой М.

Уравнение (7.16) носит название уравнения Менделеева-Клапейрона. Преобразуем его, умножив числитель и знаменатель на число Авогадро

где k = R/N_А = 8,31/6,023·10²³ = 1,38·10^-23Дж/К постоянна Больцмана,

N = N_A — число молекул в газе массой М.

Учитывая приведенные выше обозначения и определение кон­центрации n = N/V, запишем

(7.17)

Давление идеального газа зависит только от концентрации молекул и температуры газа, но не зависит от массы молекул. В случае механической смеси газов, не вступающих в химические реакции, давление определяется по формуле Р = nkT,

где n=n₁+n₂+n₃+…n_i – суммарная концентрация смеси.

Приравняем правые части уравнений (7.15.)(7.17):

и определим энергию поступательного движения молекулы

(7.18)

Средняя кинетическая энергия хаотического движения молекул идеального газа прямо пропорциональна его абсолютной температуре и является мерой интенсивности теплового движения молекул. Соответственно температура

Задания для самоконтроля знаний.

1. Записать уравнение Менделеева-Клайперона через температуру и концентрацию газа.

2. Определить температуру молекул воздуха при энергии поступательного движения 1Дж.

3. Определить давление молекулы кислорода со скоростью υ=10⁶с концентрациейn=10⁵/м³

4. Определить энергию поступательного движения молекулы воды при t=0°C.

5. Определить энергию молекул воздуха в аудитории объемом К=300м³при температуреt=20°C, и давление Р=1730мм.р.ст. Р=730 мм.р.ст.

Лекция 16