4.10 Кинетическая энергия вращательного движения

Работа силы F при повороте тела на угол dφ (рис. 4.8)

Полная работа при вращении тела в пределах изменения угловой скорости от ω₁ до ω₂

,

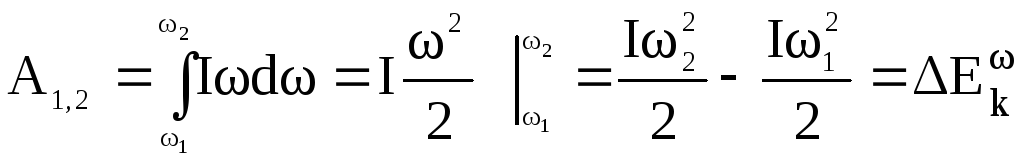где - кинетическая энергия вращательного движения.

Твердое тело может одновременно вращаться и двигаться поступательно. Тогда полная кинетическая энергия

. (4.17)

где- скорость поступательного движения центра инерции; ω – угловая скорость вращения вокруг оси.

4.11 Энергия колебательного движения тела

В процессе колебаний тела или системы тел происходят периодические переходы его кинетической энергии в потенциальную и потенциальной в кинетическую.

Кинетическая энергия

(4.18)

где – коэффициент упругости

.

Потенциальная энергия

. (4.19)

где

Полная энергия

(4.20)

Полная энергия затухающих колебаний

(4.21)

где - начальная энергия колебаний.

На рис 4.9 приведены графики изменения энергии колебательного движения в зависимости от времени.

4.12 Добротность

Затухающие колебания с течением времени изменяют свою энергию. Скорость изменения энергии определяется добротностью

, (4.22)

где Е(t) и E(t+T) - энергия колебаний в момент времени t и t+T.

Так как энергия колебаний пропорциональна квадрату амплитуды, то добротность

.

Подставим вместо А² его значение ()² тогда

. (4.23)

Используя понятия и определения характеристик затухающих колебаний приведем часто используемые формулы для вычисления добротности.

.

Задания для самоконтроля знаний.

1. _{Определить работу силы натяжения ремня Т=100Н при вращении вала R=0,2 м, если он в момент времени t=1c от начала движения имеет угловую скорость}

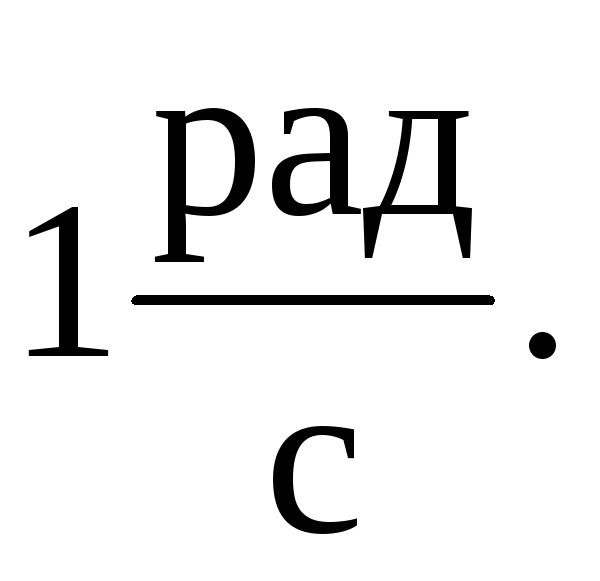
2. _{Определить массу движущегося по горизонтальной поверхности диска R=0,2 м, если при угловой скорости ω = 2 рад/с он имеет полную энергию 100 Дж.}

3. _{Определить энергию затухающих колебаний с β=2 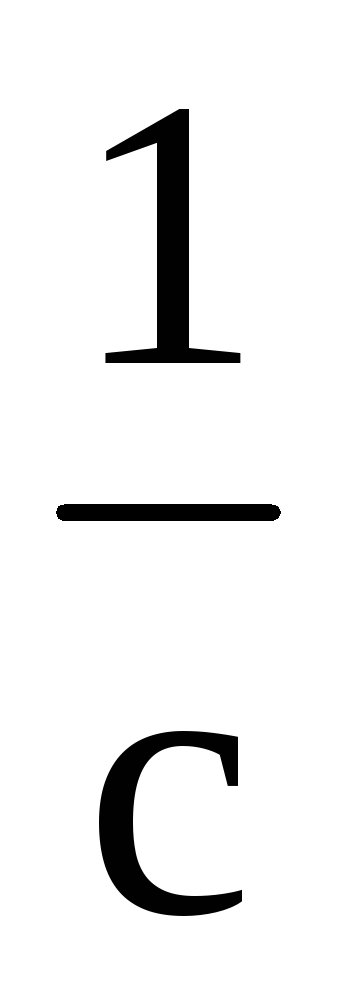в момент времени t=1мин., когда его амплитуда была 10см при коэффициенте к=100 Н/м.}

4. _{Определить добротность колебательной системы, если она имеет коэффициент затухания 2с}^-1_{, и частоту свободных колебаний π рад/с.}

Лекция 12

Глава 5. Законы сохранения в механике

5.1 Закон сохранения импульса

Тело массой m движущееся со скоростью имеет импульс

.

Согласно второму закону Ньютона

,

где -равнодействующая сила.

Если =0, то , что возможно только при. Следовательно, импульс тела остаётся постоянным, если на него не действуют силы или их равнодействующая рана нулю.

Рассмотрим взаимодействие двух тел, составляющих замкнутую систему (рис 5.1). Замкнутой системой называется такая система тел, в которой действует только внутренние силы f взаимодействия между телами. Для каждого тела этой системы импульс сил взаимодействия между телами

m₂

(5.1)

где – внутренние силы, действующие на первое и второе тело со стороны второго и первого тела соответственно;- массы и скорости взаимодействующих тел.

Из третьего закона Ньютона следует, что

.

Тогда сумма импульсов сил действующих на тело

(5.2)

При механическом взаимодействии тел в замкнутой системе изменения их импульсов попарно равны по величине и противоположны по направлению. Изменение суммарного импульса системы . Последнее равенство возможно, когда. Импульс замкнутой системы тел не изменяется с течением времени и называется законом сохранения импульса. Из закона сохранения импульса следует, что в замкнутой системе, состоящей из n тел, их векторные суммы импульсов до и после взаимодействия равны:

(5.3)

где – скоростьi тела до и после взаимодействия.

Для двух тел, при взаимодействии которых внешние силы отсутствуют или они скомпенсированы, закон сохранения импульса запишем в виде

. (5.4)

Для замкнутой системы из n тел импульс остается постоянной. Следовательно, остается постоянной и скорость центра инерции. В этом случае, центр инерции либо остается неподвижным, либо движется равномерно и прямолинейно относительно некоторой инерциальной системы отчета.