2.8 Задачи динамики материальной точки.

Задачи динамики материальной точки решаются с помощью второго закона Ньютона записанного в виде уравнений:

(2.31)

где - результирующая сила.

Выделяют два типа задач:

• по известной зависимости от времени радиус-вектора 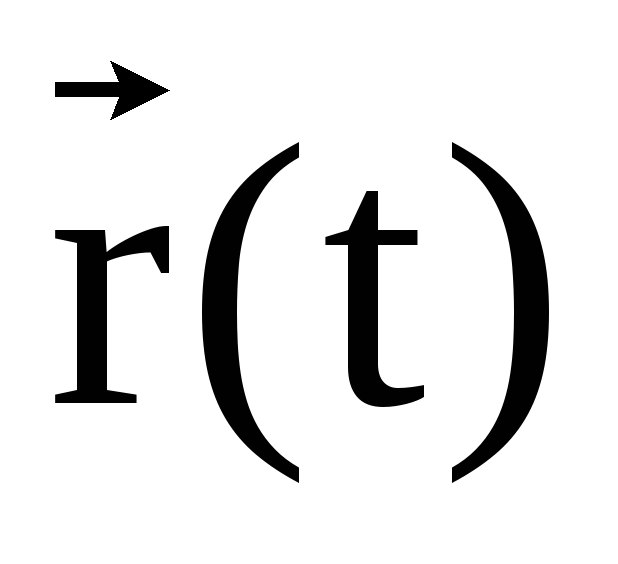, определяется результирующая сила , действующая на м.т. массойm.

• по известным начальным значениям скорости , радиус-вектора , результирующей силы действующей на м.т массойm определяется зависимость от времени радиус-вектора .

В первой задаче проводится дифференцирование по времени, во второй - интегрирование. Задачи решаются в скалярной форме с помощью проекции векторов ,,на координатные осиX,Y,Z или на касательную τ и нормаль в заданной точке траектории.

В проекциях на координатные оси уравнения (2.13) имеют вид:

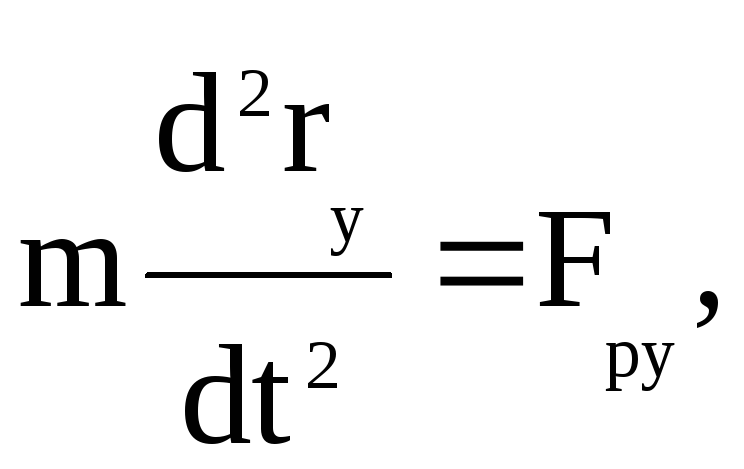
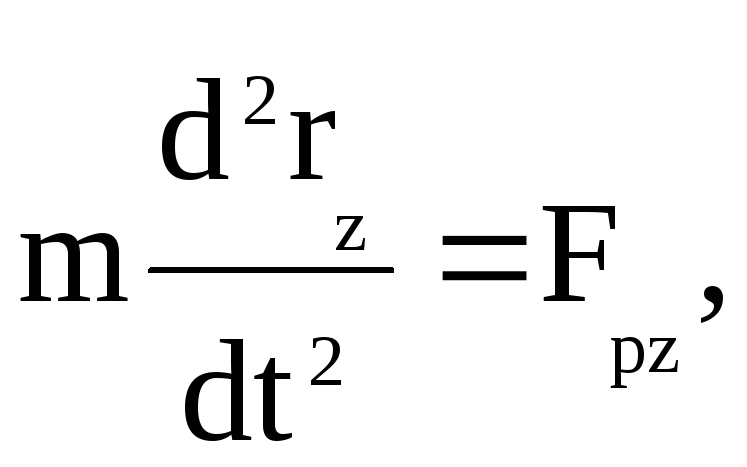
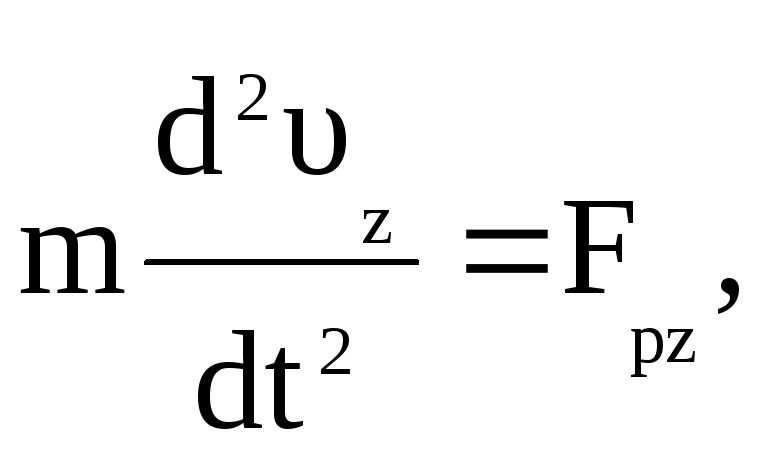(2.32)

2.9 Примеры решения типовых задач.

Задача 1. Определить вес тела Q массой m при его равноускоренном прямолинейном движении с ускорением а.

Дано: m, a

Определить: Q.

Эта задача встречается при движении груза прикрепленного к тросу строительного крана (рис 2.10).

Определим результирующую силу действующую на тело массой m прикрепленного к тросу перекинутого через

блок Б строительного крана. Для этого выберем ось X по направлению движения, и запишем уравнение динамики

в проекциях на ось Х

-mg+T=ma_х.

Решим полученное уравнение, определяя силу натяжения троса

T=m(g+a_х).

Т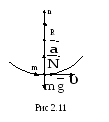ак как по определению вес равен натяжению троса при неподвижном блоке Б крана, то

Q=m(g+a) (2.33)

Задача 2. Самолет, двигаясь со скоростью делает «петлю Нестерова» радиусомR (рис 2.11). Определить силу давления летчика массой m на кресло в начале петли.

Дано: m,, R

Определить: Q.

Запишем уравнение динамики в проекциях на осьсовпадающей с ускорением

-mg+N=,

где N=m(g+).

Так как вес тела равен реакции опоры при ее равномерном движении на этом участке траектории, то

Q=m(g+) . (2.34)

Задача 3. Определить высоту h поднятия внешнего рельса железнодорожного полотна шириной l (рис 2.12) на участке пути с радиусом кривизны R и ограничением скорости поезда до .

Дано: l,, R

Определить: h.

Запишем уравнение движения состава поезда массойm с постоянной скоростью

α

.

В проекциях сил и ускорения на оси и у

запишем

n:

y: (1)

где.

Решая систему уравнений (1) найдем

где α- угол между железнодорожным полотном и линии горизонта (рис 2.12).

Учитывая, что , получим

Задача 4. Тело массой=2кг движется в направлении оси Х под действием силы. В момент времениt=0 координата тела x и его скорость равны нулю. Определить зависимость от времени координатыи скорости.

Дано: m=2 кг, ,

х₀=0, .

Найти: ,

Уравнение динамики и дифференциал скорости движения тела

Проинтегрируем левую и правую часть последнего соотношения в пределах изменения скорости и времениt:

Зависимость найдем интегрированием равенства:

Задача5. Путь пройденный телом массой задается уравнением , м. Определить зависимость силы от времени, если А=1м,B =2 м/с, С =1 м/с³.

Дано: ,

А=1м, B =2 м/с, С =1 м/с³.

Определить:.

Из уравнения динамики следует

,

где =.

Тогда .

Задания для самоконтроля знаний.

1. Поезд массой m=100 т начинает движение по участку дороги с кривизнойR=100м, увеличил свой путь в соответствии с уравнениемS(t)=5t². Найти силу тяги локомотива в момент времениt=5c.

2. Грузовой автомобиль массой m=5т, без груза может увеличивать скорость за времяt=1 мин до 36 км/ч, а с грузом до 20 км/ч. Определить массу грузаm₂.

3. С какой скоростью должен летать самолет в верхней точки петли Нестерова радиусом R=300м, чтобы летчик испытал невесомость.