2.8. Основной закон динамики поступательного движения и закон сохранения импульса для системы материальных точек

1.Рассмотрим физическую си­стему, состоящую изNматериальных точек (рис. 2.4). Пусть помимо внутренних сил , наi-ю частицу действуют внешние силы, результирующая которых равна . Запишем уравнения движения для каждой из частиц:

;

;

………………………………………………………………

;

………………………………………………………………

.

Сложим эти N уравнений. Вследствие того, что (согласно третьему закону Ньютона) и т.д., справа останутся только внешние силы. Таким образом, мы приходим к соотношению

. (2.9)

Сумму импульсов частиц, стоящую под знаком производной в левой части, назовем импульсом системы. Обозначив его , получим

. (2.10)

Из (2.10) следует, что импульс является аддитивной величиной.

Запишем соотношение (2.9) в виде

. (2.11)

Это уравнение выражает основной закон поступательного движения для системы материальных точек: скорость изменения импульса физической системы равна суммарной внешней силе.

2. Из уравнения (2.11) следует, что в отсутствии внешних сил

, (2.12)

т.е. суммарный импульс замкнутой системы тел остается постоянным (закон сохранения импульса для системы материальных точек). Иначе говоря, импульс системы тел может быть изменен только за счет действия внешних сил.

Отметим, что импульс остается постоянным и для незамкнутой системы при условии, что внешние силы в сумме дают нуль. В случае, когда сумма внешних сил не равна нулю, но проекция этой суммы на некоторое направление равна нулю, сохраняется составляющая импульса в этом направлении.

Вообще, в механике рассматривается три закона сохранения: импульса, момента импульса и энергии. Эти законы отражают фундаментальные свойства пространства-времени.

Закон сохранения импульса связан с однородностью пространства (равноправием различных его точек): физические процессы в различных точках пространства протекают одинаково.

Закон сохранения момента импульса (рассматривается в разделе 3) связан с изотропностью пространства (равноправием различных направлений).

Закон сохранения энергии (рассматривается в разделе 4) связан с однородностью времени (равноправием различных моментов времени).

Важнейшая роль законов сохранения как инструмента решения физических задач обусловлена рядом причин:

а) законы сохранения не зависят ни от траекторий частиц, ни от характера действующих сил. Поэтому они позволяют получить ряд общих и существенных заключений о свойствах различных механических процессов, не вникая в их детальное рассмотрение с помощью уравнений движения. Если, например, выясняется, что такой-то процесс противоречит законам сохранения, то можно утверждать: этот процесс невозможен, и бессмысленно пытаться его осуществить;

б) тот факт, что законы сохранения не зависят от характера действующих сил, позволяет использовать их даже тогда, когда силы вообще не известны. В этих случаях законы сохранения являются единственным и незаменимым инструментом исследования. Так, например, обстоит дело в физике элементарных частиц;

в) даже в тех случаях, когда силы в точности известны, законы сохранения могут оказать существенную помощь при решении многих задач о движение частиц. Хотя все эти задачи могут быть решены с помощью уравнений движения, привлечение законов сохранения очень часто позволяет получить решение наиболее простым и изящным путем, избавляя нас от громоздких и утомительных расчетов. Поэтому при решении новых задач обычно принято придерживаться следующего порядка: прежде всего один за другим применяют соответствующие законы сохранения и, только убедившись, что этого недостаточно, переходят затем к решению с помощью уравнения движения.

Законы сохранения относятся к числу фундаментальных принципов физики. Роль этих законов особенно возросла после того, как выяснилось, что они далеко выходят за рамки механики и представляют собой универсальные законы природы.

3. Вернемся к уравнению движения системы материальных точек. При поступательном движении удобно пользоваться понятием центра масс физической системы. Преобразуем выражение (2.10) для импульса системы точек (– радиус-вектор, задающий положениеk-ой материальной точки):

.

Точку c, положение которой задается уравнением

, (2.13)

будем называть центром масс (или центром инерции) системы. Центр масс имеет смысл точки приложения всех действующих на систему массовых сил.

Координаты центра масс определяются следующим образом:

Например, для изображенной на рис. 2.5 системы центр масс имеет координаты:

;.

Продифференцировав по времени выражение (2.13), получим формулу для вычисления скорости центра масс:

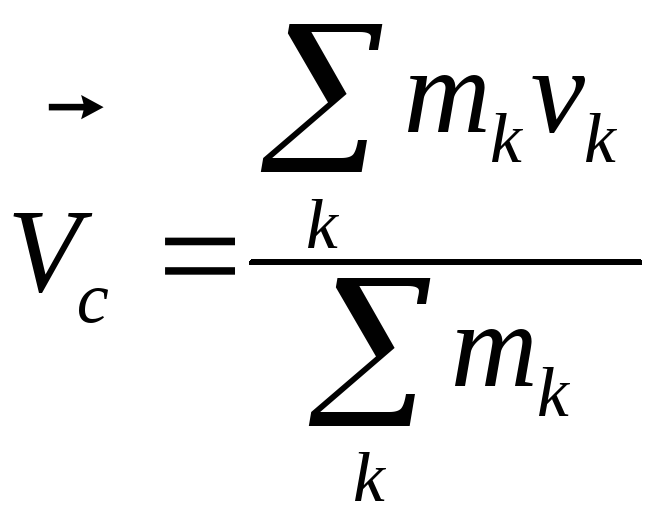. (2.14)

Тогда импульс системы можно определить следующим образом:

. (2.15)

По аналогии с уравнением движения отдельной частицы можно записатьуравнение движения центра масс системы материальных точек:

, (2.16)

где – суммарная внешняя сила, действующая на систему материальных точек; – импульс системы;M – масса системы материальных точек; – скорость движения центра масс системы;– ускорение центра масс.