5.2. Гармонические колебания

Рассмотрим систему, представляющую собой шарик массой m, подвешенный на нити. Сообщим шарику смещение x = A, после чего предоставим систему самой себе. Под действием квазиупругой силы (силы, зависящие от смещения по закону F_x =  kx, независимо от их природы называются квазиупругими) шарик будет двигаться к положению равновесия с возрастающей скоростью

.

При этом потенциальная энергия системы будет убывать, но зато появится все возрастающая кинетическая энергия

.

Достигнув положения равновесия, шарик продолжит движение по инерции. Это движение будет замедленным и прекратится тогда, когда кинетическая энергия полностью перейдет в потенциальную, т.е. когда смещение шарика станет равным (А). Затем аналогичный процесс будет протекать при движении шарика в обратном направлении. Если трение в системе отсутствует, то полная энергия должна сохраняться, и шарик будет двигаться в пределах от х = А до х =  А неограниченно долго.

Уравнение второго закона Ньютона для шарика имеет вид

. (5.1)

Введя обозначение

, (5.2)

преобразуем уравнение (5.1) следующим образом:

. (5.3)

Итак, при отсутствии сил трения движение под действием квазиупругой силой описывается уравнением (5.3). Это уравнение представляет собой дифференциальное уравнение собственных незатухающих колебаний.

5.2.1. Кинематические характеристики гармонического колебания

Общее решение уравнения (5.3) имеет вид:

x = A cos (ω₀t + α) , (5.4)

где А и α – произвольные постоянные.

Таким образом, смещение х изменяется со временем по закону косинуса. Следовательно, движение системы, находящейся под действием силы вида F =  kx, представляет собой гармоническое колебание. Реальные колебания бывают гармоническими, если они малые, любые конечные колебания ангармоничны.

Г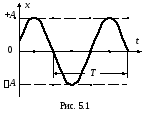рафик гармонического колебания, т.е. график функции (5.4), показан на рис. 5.1. По горизонтальной оси отложено времяt, по вертикальной оси – смещение х.

Поскольку косинус изменяется в пределах от –1 до +1, значения х лежат в пределах от –А до +А. Величина наибольшего отклонения системы от положения равновесия называется амплитудой колебания. Амплитуда А  постоянная положительная величина. Ее значение определяется величиной начального отклонения или толчка, которым система была выведена из положения равновесия.

Величина (₀t+), стоящая под знаком косинуса, называется фазой колебания. Она характеризует состояние колеблющейся системы в произвольный момент времениt. Постоянная, характеризующая состояние системы в начальный момент времениt= 0, называется начальной фазой колебания. Поскольку косинус – периодическая функция с периодом 2, различные состояния системы, совершающей гармонические колебания, повторяются через такой промежуток времени Т, за который фаза колебания получает приращение, равное 2(рис.5.1). Этот промежуток времени называется периодом колебания. Он может быть определен из условия , откуда

. (5.5)

Число колебаний, совершающихся в единицу времени, называется частотой колебания .Частота связана с периодом колебания Т следующим образом:

. (5.6)

За единицу частоты принимается частота такого колебания, период которого равен 1 с. Эту единицу называют герцем (Гц). Частота в 10³ Гц называется килогерцем (кГц), в 10⁶ Гц – мегагерцем (МГц).

Из соотношения (5.5) следует, что:

. (5.7)

Таким образом, ₀дает число колебаний за2 секунд. Величина ₀называется циклической (круговой) собственной частотой колеблющейся системы. Она связана с частотой  соотношением

₀ = 2 . (5.8)

Продифференцировав (5.4) по времени, получим выражение для скорости тела, совершающего колебательное движение:

v = A₀ sin (₀t + ) = A₀ cos (₀t +  +) . (5.9)

Как видно из (5.9), скорость также изменяется по гармоническому закону, причем амплитуда колебаний скорости A₀. Из сравнения (5.4) и (5.9) следует, что скорость с амплитудой А₀ опережает смещение по фазе на .

Продифференцировав (5.9) по времени еще раз, найдем выражение для ускорения этого тела:

а = Acos (₀ t +) =

=A cos (₀ t +  +) . (5.10)

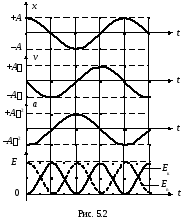
Как следует из (5.10), ускорение и смещение меняются в противофазе. Это означает, что в тот момент, когда смещение достигает положительного наибольшего значения, ускорение достигает наибольшего по модулю отрицательного значения, и наоборот.

На рис. 5.2 сопоставлены графики для смещения, скорости и ускорения.