1.2. Вращательное движение

Вращательным движением твердого тела вокруг неподвижной оси называется движение, при котором все точки тела движут­ся по окруж­ности, центры которых лежат на од­ной прямой, называемой осью вра­щения. Ось вращения перпен­дику­ляр­на плоскостям, в ко­торых лежат эти окружности. Она может проходить сквозь тело или лежать за его пре­де­ла­ми. Если ось вращения проходит сквозь тело, то те точки тела, которые лежат на этой оси, во время движения тела остаются в покое.

При вращательном движении абсолютно твердого тела нельзя поль­­зоваться моделью материальной точ­ки, ибо разные точки тела движутся по окружностям разного радиуса, т.е. их пути и скорости различны (рис. 1.4). В силу этой же причины враще­ние твердого тела (как целого) не может быть охарак­те­ри­зо­ва­но линей­ным переме­щением и линей­ной ско­ростью, как это было сделано в посту­пательном дви­жении. Вместе с тем, нетрудно заметить, что радиусы-век­то­ры, соеди­ня­ющие все точки твер­дого тела с центрами описы­ва­е­мых ими окруж­ностей, пово­ра­чи­­ва­ются за один и тот же про­ме­жу­ток времени на одинаковый угол (см. рис. 1.4). Следовательно, все точки абсо­лют­но твердого тела во вращательном движении проходят одинаковые уг­ло­вые пути и имеют одинаковые угло­вую скорость и уг­ловое ускорение. Поэтому в качестве кинематических характеристик вра­ща­тельного движе­ния тела должны быть выбраны век­тор углового пере­мещения, угловая скорость и угловое ускорение.

При малых поворотах тела угол поворота можно рассматривать как векторную величину , численно равную модулю d, и направленную вдоль оси вращения ОО^/ так, чтобы из конца вектора поворот тела был виден против часовой стрелки (правило буравчика) (см. рис. 1.5).

Угловой скоростью тела называют вектор , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения по правилу буравчика, т.е. так же, как вектор угла поворота.

. (1.23)

Угловая скорость характеризует направление и быстроту вращения тела как целого вокруг оси. Если = const, то движение тела называют равномерным вращением вокруг неподвижной оси.

Скорость произвольной точки М тела, вращающегося с угловой скоростью , называют линейной скоростью этой точки. За время dt точка М проходит по дуге окружности радиуса R путь ds = vdt =Rd так, что

. (1.24)

Из рис. 1.5 видно, что вектор направлен перпендикулярно и к и к радиусу-вектору в ту же сторону, что и векторное произведение . Так как векторы и взаимно перпендикулярны, то || = R = v.

Следовательно,

. (1.25)

Так как в случае вращения тела вокруг неподвижной оси за начало координат, из которого проводят радиусы-векторы , можно выбрать любую точку оси вращения, то выражение (1.25) можно переписать в виде:

. (1.26)

Для характеристики неравномерного вращения тела вводится понятие углового ускорения.

Угловым ускорением называют вектор , характеризующий быстроту изменения угловой скорости со временем и численно равный первой производной угловой скорости по времени:

. (1.27)

В случае вращения тела вокруг неподвижной оси изме­нение вектора обусловлено только изменением его чис­лен­ного значения. При этом вектор направлен вдоль оси вращения (рис. 1.6): в ту же сторону, что и , при уско­рен­­ном вращении () и в про­тиво­полож­ную сторону  при за­мед­лен­ном вращении ().

Наряду с понятием угловой ско­рости пользуются понятиями периода и частоты вращения.

Периодом вращения Т называют промежуток време­ни, в течение которого тело со­вершает один полный оборот, т.е. поворачивается на угол 2 .

Частотой вращения n называют число оборотов, совершаемых телом за одну секунду.

Связь между , T и n имеет вид

. (1.28)

Угол поворота в системе СИ измеряется в радианах (рад), угловая скорость  в радианах в секунду (рад/с), угловое ускорение  в радианах в секунду в квадрате (рад/с²).

Выразим тангенциальное и нормальное ускорение произвольной точки тела, вращающегося вокруг неподвижной оси, через угловую скорость и угловое ускорение тела:

, (1.29)

. (1.30)

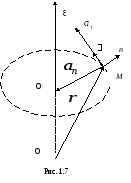
Из рис. 1.7 и уравнения (1.29) следует, что вектор равен векторному произведению вектора углового ускорения на радиус-вектор , соединяющий произвольную точку на оси вращения с точкой М:

. (1.31)

Вектор нормального ускорения направлен к оси вращения, т. е. в противо­по­ложную сторону от :

. (1.32)

В табл. 1.1, 1.2 сопоставляются характеристики и законы поступательного и вращательного движения материальной точки. Аналитическое и графическое описа­ния этих двух видов движений аналогичные. Кроме того, в таблицах приводятся формулы, связывающие характеристики поступательного и вращатель­ного движений материальной точки. В табл. 1.3 даны единицы измерения кинематических характерис­тик поступательного и вращательного движений.

Таблица 1.1

Сопоставление характеристик

поступательного и вращательного движения материальной точки.

поступательное движение	характеристики	вращательное движение
Путь s Скорость v = ds/dt Тангенциальное ускорение а = dv/dt Нормальное ускорение аn = v2/R Полное ускорение	s = R  v = R  а = R  аn=  R	Угловой путь  Угловая скорость  = d/dt Угловое ускорение  = d/dt

Таблица 1.2

Виды движения (уравнения и графики)

Поступательное движение	Вращательное движение
Равномерное
;;.	;;.
Окончание табл. 1.2
Поступательное движение				Вращательное движение
Равнопеременное
; ;	; ;
t
Неравномерное

Таблица 1.3

Единицы измерения и кинематические характеристики

поступательного и вращательного движений

Наименова-ние харак­те­ристики	Обозначение и определяющее уравнение	Название единицы измерения	Сокращенное обозначение единицы измерения
Длина	l	метр (основная ед.)	м
Время	t	cекунда(основная ед.)	с
Скорость	v = dl/d t	метр в секунду	м/с
Ускорение	a = dv/dt	метр в секунду в квадрате	м/с2
Плоский угол		радиан	рад
Угловая скорость	 = /t	радиан в секунду	рад/с
Угловое ускорение	 = /t	радиан в секунду в квадрате	рад/с2
Частота		секунда в минус первой степени	с-1

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Какое движение называется механическим?

2. Что понимают под системой отсчета? Для чего нужны систе­мы отсчета?

3. Какое движение называется поступательным?

4. Что называется материальной точкой?

5. Что понимают под траекторией движения? На какие виды делится механическое движение по характеру траектории?

6. Что такое путь? Скалярная или векторная это величина?

7. Что такое вектор перемещения?

8. Что отражает уравнение (задан ли вид траектории): а) ; б) r = =r(t); в)

9. Что такое скорость механического движения?

10. Что называется: а) средней скоростью механического движения; б) мгновенной скоростью механического движения?

11. Как записать мгновенную скорость переменного движения: а) векторным способом; б) координатным способом (величина и направление)?

12. Как направлена скорость криволинейного движения точки?

13. Как по графику скорости найти путь?

14. Что характеризует ускорение поступательного движения? Чем опре­де­ля­ются величина и направление ускорения?

15. Какое ускорение называется: а) средним; б) мгновенным?

16. Как направлен вектор ускорения по отношению: а) к траектории движения (в некоторой точке); б) к вектору скорости, в) к равнодействующей силе?

17. Как записать ускорение поступательного движения: а) векторным способом; б) координатным способом?

18. Что характеризует: а) касательная составляющая ускорения, б) нормальная составляющая ускорения?

19. Каковы величина и направление: а) касательной составляющей ускорения; б) нормальной составляющей ускорения?

20. Может ли точка, двигающаяся по кривой, обладать: а) танген­ци­аль­ным ускорением, равным нулю, б) нормальным ускорением, равным нулю?

21. Может ли полное ускорение точки, двигающейся по кривой, быть направленным в сторону: а) вогнутости траектории; б) выпуклости траектории?

22. Каковы величина и направление полного ускорения тела, брошенного под углом к горизонту?

23. Каков характер движения тела, брошенного: а) в вертикальном напра­в­ле­нии; б) в горизонтальном направлении; в) под углом к горизонту?

24. Написать зависимость скорости от времени для тела, бро­шенного: а) в вертикальном направлении; б) в горизонтальном направлении; в) под углом к горизонту?

25. Какое движение называется вращательным?

26. Что называется абсолютно твердым телом?

27. Чем определяется положение вращающегося тела в прост­ранстве?

28. Что называется угловой скоростью? Скалярная или вектор­ная это величина?

29. Как могут быть представлены: а) средняя угловая скорость; б) мгно­вен­ная угловая скорость?

30. Какое вращение называется: а) равномерным; б) равнопеременным; в) пе­­ременным?

31. Что называется угловым ускорением?

32. Как выражаются среднее и мгновенное угловые ускорения при любом переменном вращении тела?

33. Как могут быть представлены при равнопеременном вращении: угол поворота в функции времени, угловая скорость, угловое ускорение?

34. Как строятся векторы: а) угловой скорости; б) углового ускорения?

35. Как связаны: а) путь, пройденный какой-либо точкой вращающегося тела; б) ее линейная скорость; в) тангенциальное ускорение; г) нормальное ускорение; д) полное ускорение с соответствующими угловыми характеристиками?

36. В каких единицах в СИ измеряются: а) линейный путь; б) угловой путь; в) линейная скорость; г) угловая скорость; д) линейное ускорение; е) угловое ускорение?

37. Какой формулой выражается связь угловой скорости и числа оборотов вала в единицу времени?

38. Какой формулой выражается связь угловой скорости с пе­риодом вращения?