5.5. Затухающие колебания

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. В простейшем случае сила сопротивления пропорциональна величине скорости:

. (5.49)

Здесь r  постоянная величина, называемая коэффициентом сопротивления среды. Знак минус обусловлен тем, что сила и скорость v имеют противоположные направления, поэтому их проекции на ось х имеют разные знаки.

Уравнение второго закона Ньютона при наличии сил сопротивления имеет вид

. (5.50)

Применив обозначение

, (5.51)

(r  коэффициент сопротивления среды, т.е. коэффициент пропорциональности между скоростью и силой сопротивления;k – коэффициент квазиупругой силы; ₀ – собственная частота колебания системы), перепишем уравнение (5.50) следующим образом:

. (5.52)

Это дифференциальное уравнение описывает затухающие колебания системы.

При не слишком сильном трении общее решение уравнения (5.52) имеет вид:

x = A₀ e^{ t} cos ( t+) . (5.53)

Здесь А₀ и   произвольные постоянные;

, (5.54)

  частота, с которой система совершает затухающие колебания.

Н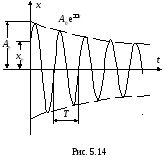а рис. 5.14 представлен график функции (5.53). Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точких.

В соответствие с видом функции (5.53) движение системы можно рассматривать как гармоническое колебание частоты  с амплитудой, изменяющейся по закону

А(t) = А₀ e^{ t}. (5.55)

Верхняя из пунктирных кривых на рис. 5.14 дает график функции А(t), причем величина А₀ представляет собой амплитуду в начальный момент времени. Начальное смещение х₀ зависит, кроме А₀, также от начальной фазы :

х₀ =А₀ cos  .

Скорость затухания колебаний определяется величиной = r/2m, которую называют коэффициентом затухания.

Определим физический смысл коэффициента затухания. Для этого найдем время , за которое амплитуда уменьшается в е раз. По определению е^t = e^1, откуда  = 1. Следовательно, коэффициент затухания обратно пропорционален по величине тому промежутку времени , за который амплитуда уменьшается в е раз (е = 2,72 – основание натурального логарифма).

Согласно формуле (5.5) период затухающих колебаний

. (5.56)

При незначительном сопротивлении среды (² << ) период колебаний практически равенТ₀ = 2/₀. С ростом коэффициента затухания период колебаний увеличивается.

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период

. (5.57)

Это отношение называют декрементом затухания, а его логарифм логарифмическим декрементом затухания ():

. (5.58)

Определим физический смысл логарифмического декремента затухания. Для этого перепишем выражение (5.55) с учетом (5.58) в виде

А= А₀ е^{ (/Т) t} .

За время , за которое амплитуда уменьшается в е раз, система успевает совершить N_е = /Т колебаний. Из условия е^{(/Т) t} = е^1 получается, что . Следовательно,логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.