Вопросы для самоконтроля

1. В каких случаях нельзя пользоваться законами Ньютона?

2. Сформулировать первый закон Ньютона.

3. Что такое инерция?

4. Какая система отсчета называется: а) инерциальной; б) неинерциальной?

5. Как формулируется принцип относительности Галилея?

6. Какие динамические характеристики описывают поступатель­ное движение?

7. Дать определение силы.

8. Какие виды сил в механике Вы знаете?

9. Какая сила называется упругой? Чему она равна? Каковы ее свойства?

10. Что такое сила тяготения? Чему она равна? Каковы ее свойства?

11. Какая сила называется силой трения? Чему она равна? Каковы ее свойства?

12. Какую величину называют импульсом силы?

13. Что такое масса? Какими свойствами она обладает?

14. Всегда ли масса постоянна в процессе движения тела?

15. Какая величина называется импульсом тела?

16. Как найти изменение импульса, если тело движется по кривой?

17. Сформулировать второй закон Ньютона в самой общей форме и записать его математически.

18. Сформулировать и записать математически второй закон Ньютона для частного случая движения тела постоянной массы (m = const).

19. В чем заключается принцип суперпозиции для сил?

20. Сформулировать третий закон Ньютона. В чем суть этого закона?

21. Как зависит характер поступательного движения тела от вида действующей силы? Приведите примеры.

22. Какая система тел называется замкнутой (изолированной), незамкнутой?

23. Какие силы называются внешними, внутренними?

24. Сформулируйте и запишите математически закон сохранения импульса (количества движения): а) для отдельного тела; б) для системы тел.

25. Напишите уравнение движения тела с переменной массой и поясните физическое содержание входящих в него величин.

26. Что такое «реактивная сила»? От каких величин и как она зависит?

27. Какое движение называется реактивным?

28. От каких величин и как зависит скорость, приобретенная ракетой в процессе движения?

3. Динамика вращательного движения твердого тела

3.1. Основной закон динамики вращательного движения

Любое тело или систему тел можно мысленно представить в виде системы материальных точек – достаточно малых частей этих тел. Рассмотрим произвольную механическую систему, состоящую из n материальных точек. Пусть m_i – масса i-й точки системы, а – радиус-вектор, проведенный в эту точку из начала координатО неподвижной инерциальной системы отсчета. Обозначим через силу, действующую наi-ю точку со стороны k-й материальной точки системы (внутренние силы), а через – равнодействующую всех внешних сил (сил, действующих на рассматриваемую систему извне), приложенных к i-й точке

. (3.1)

Легко видеть, что знак производной по времени в левой части этого уравнения можно вынести за знак векторного произведения. В самом деле,

,

потому что

,

как векторное произведение двух одинаково направленных векторов.

Следовательно, уравнение (3.1) можно переписать в виде

. (3.2)

Векторное произведение радиуса-вектора материальной точки на ее импульс называют моментом импульса этой материальной точки относительно точки О

. (3.3)

Он направлен перпендикулярно к плоскости, проведенной через векторы и , и образует с ними правую тройку векторов (при наблюдении из конца видно, что вращение по кратчайшему расстоянию от к происходит против часовой стрелки, рис. 3.1,а).

Векторное произведение радиуса-вектора , проведенного в точку приложения силы, на эту силу называют моментом силы относительно точки О:

. (3.4)

Векторы , , образуют правую тройку (рис. 3.1, б). Численное значение момента силы

M_i = F_i r_i sin _i = F_i l_i , (3.5)

где _i – угол между векторами и , а l_i = r_i sin _i – длина перпендикуляра, опущенного из точки О на линию действия силы . Величина l_i называется плечом силы . Если линия действия силы проходит через точку О, то l_i = 0 и момент силы относительно точки О равен нулю.

Из (3.2), (3.3), и (3.4) следует, что скорость изменения момента импульса i-й материальной точки

. (3.6)

Сложим почленно все эти уравнения, записанные для каждой из n материальных точек системы:

. (3.7)

Векторную сумму моментов всех внешних сил, приложенных ко всем материальным точкам системы, называют результирующим, или главным моментом внешних сил относительно точки О:

. (3.8)

Векторную сумму моментов импульсов всех материальных точек системы называют моментом импульсасистемы относительно точкиО:

. (3.9)

Так как производная от суммы равна сумме производных от всех слагаемых, то

. (3.10)

Наконец, векторная сумма моментов относительно точки О всех внутренних сил взаимодействия между материальными точками системы равна нулю:

. (3.11)

Это связано с тем, что по третьему закону Ньютона силы и численно равны, имеют общую линию действия, но направлены противоположно. Поэтому их моменты и относительно точкиО численно равны и противоположны по направлению.

На основании соотношений (3.8), (3.10) и (3.11) уравнение (3.7) можно записать в следующей форме:

. (3.12)

Таким образом, скорость изменения момента импульса системы относительно неподвижной точки равна результирующему моменту относительно той же точки всех внешних сил, действующих на систему.

Соотношение (3.12) справедливо, в частности, для твердого тела, закрепленного в точке О. В этом случае оно выражаетосновной закон динамики тела, вращающегося вокруг неподвижной точки. Из него следует, что момент импульсаявляется основной динамической характеристикой тела, вращающегося вокруг неподвижной точки.

Пусть теперь твердое тело закреплено в двух неподвижных точках: О и О₁ так, что оно может вращаться вокруг неподвижной оси Оz, проходящей через эти точки. В этом случае, составляющие момента относительно точкиО, направленные вдоль осей Ох и Оy, компенсируются соответствующими моментами сил реакции закрепления в точке О₁. Поэтому вращение тела вокруг оси 0z происходит под действием составляющей M_z момента внешних сил относительно точки О. Из (3.12) следует, что уравнение движения тела имеет вид

, (3.13)

где L_z и M_z – составляющие векторов момента импульса тела и результирующего момента внешних сил относительно точки О, направленные вдоль неподвижной оси Оz вращения тела и называемые, соответственно, моментом импульса тела относительно оси Оz и результирующим моментом внешних сил относительно той же оси. Уравнение (3.13) выражает основной закон динамики для тела, вращающегося вокруг неподвижной оси: скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой оси всех внешних сил, действующих на тело.

Из этого закона следует, что основной динамической характеристикой тела, вращающегося вокруг неподвижной оси, является момент импульса тела относительно этой оси.

Найдем выражение для момента импульса L_z тела, вращающегося вокруг неподвижной оси Оz с угловой скоростью . Так как , то .

Из рис. 3.2 видно, что радиус-вектор i-й материальной точки

,

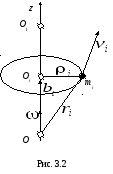
где – вектор, проведенный из точки О в точку О_i, лежащую на оси вращения Оz и являющуюся центром окружности, по которой движется рассматриваемая i-я точка тела. Поэтому

.

Вектор перпендикулярен к вектору , т.е. его составляющая вдоль оси Оz равна нулю. Векторы , ивзаимно перпендикулярны и лежат в плоскости, перпендикулярной оси вращения тела. Поэтому вектор численно равен _i m_i v_i = ²_i,m_i  и направлен вдоль оси вращения тела в ту же сторону, что и вектор . Таким образом, L_iz = ²_i m_i  и

. (3.14)