1. Закон сохранения массы

1. Три теоремы об интегралах

Теорема 1. Дана функция. Рассмотрим подобласть.

Если

,

то

.

◄ Докажем утверждение теоремы методом от противного. Если функция непрерывна в точкеи, то функциясохраняет знак в некоторой окрестноститочки, следовательно,,. Полученное противоречие доказывает теорему. ►

Теорема 2. Для векторного поля

или, в другой записи,

,

где – единичный вектор внешней нормали поверхности, ограничивающей объем, в котором определен вектор.

В координатах эта формула принимает вид

.

Замечание. Обобщение формулы Гаусса-Остроградского

В математическом анализе формула Гаусса-Остроградского доказана в следующем виде

.

Покажем, что формула будет верна, если скалярные функции ,изаменить на векторные, и.

Для доказательства каждую векторную функцию , инадо разложить по базису и применить указанную формулу к каждой компоненте

.

Итак, формула справедлива как для скалярных, так и для векторных функций ,и.

.

В дальнейшем нам понадобятся понятия контрольного объема (поверхности), скорости поверхности, переноса параметра сплошной среды через поверхность и правило дифференцирования по времени интеграла по подвижному пространственному объему.

Контрольным объемом называется выделенный объем пространства, его границаназываетсяконтрольной поверхностью.

Для определения скорости поверхности в некоторой точкерассмотрим положения поверхностив два момента времени:и(Рис. 1.7.1). Выберем окрестность точки, площадкуи проведем в точкевнешнюю нормаль. Отрезок нормали между поверхностямииобозначим.Скоростью перемещения поверхностив точкеназывается

.

Переносомпараметрачерез площадкус нормальюназывают величину, равную

,

где – скорость сплошной среды,– секундный расход среды через.Перенос через поверхностьопределяется интегралом

.

Теорема 3. (О дифференцировании интеграла по подвижному объему).

Рис. 1.7.1

Рассмотрим пространственный объем , ограниченный поверхностью(Рис. 1.7.1). Имеет место формула

где – скорость поверхности,– произвольная функция.

◄ Рассматриваемый объем в момент времени обозначим, а в момент времени–.

Представим объем в виде

.

.

Разобьем объем на цилиндры с основаниеми высотой(Рис. 1.7.1). Объем цилиндра с основаниеми высотойравен

.

Тогда интеграл по объему можно преобразовать в интеграл по поверхности:

,

. ►

Следствия.

1. Пусть объем является материальным,,, тогда скорость поверхностиравна, где– скорость сплошной среды, и формула дифференцирования принимает вид

.

2. Используя теорему Гаусса-Остроградского, формулу можно переписать иначе:

.

.

3. Если предположить, что в момент времени контрольный объемсовпадает с материальным

,,

то из формул и следует

Замечание. Получим еще одну формулу дифференцирования интеграла по материальному объему, когда подынтегральная функция имеет вид

,

где – скалярная или векторная функция.

.

Обратим внимание, что под интегралом стоит материальная производная, так как при интегрировании параметр вычисляется для фиксированной материальной частицы.

Итак,

.

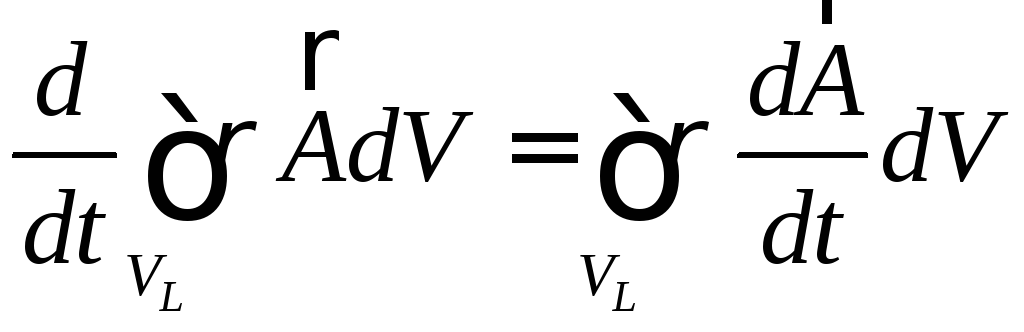2. Закон сохранения массы

В ньютоновской механике любой материальный объем сохраняет свою массу во времени.

Получим закон сохранения массы в дифференциальной форме. Пусть – произвольный материальный объем с переменной плотностью(Рис. 1.7.2).

Рис. 1.7.2

Масса, заключенная в этом объеме .

Согласно закону сохранения массы

.

Применим следствие 2 из теоремы 3, т.е. формулу

.

Таким образом,

.

Так как объем выбран произвольно, то по теореме 1

Это дифференциальное уравнение, выражающее закон сохранения массы, называется уравнением неразрывности.

Полученная форма его записи называется дивергентной. Такая форма уравнений в частных производных повышает эффективность процедуры решения с помощью численных методов.

Преобразуем выражение для

.

Тогда

,

Перепишем это равенство иначе

.

Такая формула уравнения неразрывности делает прозрачным его физический смысл: скорость относительного изменения плотности материальной частицы равна скорости относительного изменения ее объема, взятой с противоположным знаком.

Уравнение баланса массы можно записать и для пространственного объема , ограниченного поверхностью.

В силу следствия 3 из теоремы 3 (формула )

,

где – материальный объем, который в момент временисовпадает с объемом. Так как первый интеграл справа равен нулю, то баланс массы для контрольного объемаимеет вид

.

Если контрольный объем неподвижен, то . Из интегрального уравнения можно снова получить дифференциальное уравнение неразрывности, рассуждая так же, как в случае материального объема.

Уравнение неразрывности, которое было получено, справедливо при эйлеровом описании движения сплошной среды. При лагранжевом описании оно будет выглядеть иначе.