2. Эйлерово и лагранжево описания движения сплошной среды

Эйлеровыми переменныминазываются координаты точки пространства (геометрические координаты) и время (Рис. 1.2.1.).Лагранжевыми переменныминазываются координаты материальной точки (материальные координаты) и время . Удобно задавать материальные координаты следующим образом: материальные координаты частицы равны ее геометрическим координатам в начальный момент времени:

при .

При эйлеровом описаниилюбой параметрсплошной среды задается как функция эйлеровых переменных . Тем самым можно определить значения параметров сплошной среды в любой момент времени и в любой точке пространства, занятого сплошной средой.

Рис. 1.2.1.

Часто для решения задачи оказывается более удобным описание, связанное не с геометрическим пространством, а со сплошной средой. В этом случае используют лагранжево описание.

При лагранжевом описаниилюбой параметрсплошной среды задается как функция лагранжевых переменных . Лагранжево описание позволяет найти параметры любой материальной частицы.

1. Вычисление скорости материальной частицы

Рассмотрим материальную частицу с координатой . Тогда ее геометрические координаты будут функциями времени и зададут траекторию этой частицы. Следовательно,при эйлеровом описании скорость частицы . Нопри лагранжевом описании и .Некоторые студенты пишут, это грубая ошибка!

2. Материальная производная

Материальной производнойназывается производная по времени какого-либо параметра фиксированной материальной частицы.

Материальную производную в литературе также называют субстанциональной или индивидуальной производной.

При лагранжевом описании материальная производная вычисляется как частная производная по времени:

.

Найдем материальную производную параметра при эйлеровом описании. Для этого рассмотрим материальную частицу с координатой. При движении ее материальные координаты не изменяются, но пространственные координаты являются функцией времени

для.

Вычислим материальную производную

.

Таким образом, материальная производная при эйлеровом описании совпадает с полной производной.

Учитывая определение скорости, можно записать

,

где .

3. Переход от эйлерова описания к лагранжевому и обратно

Эйлерово и лагранжево описание являются равносильными и нужно уметь переходить от одного описания к другому. Рассмотрим этот вопрос на примере.

Пример 1.Дано эйлерово описание движения сплошной среды

Требуется найти его лагранжево описание.

Решение.

Зададим материальные координаты так, что в начальный момент движения они равны геометрическим, т.е. при . Учитывая определение скорости и начальное условие, имеем задачу Коши для системы уравнений

,

.

Решим эту задачу.

Закон движения в лагранжевых переменных найден.

Таким образом, чтобы перейти от эйлерова описанию к лагранжевому, необходимо составить систему и решить ее с учетом начальных условий.

Убедимся, что и– взаимнооднозначные зависимости, т.е. в любой момент времени в любой точке пространства находится только одна материальная частица. Для этого нужно вычислить якобиан и убедиться, что он никогда не обращается в нуль.

для любого момента времени.

Следовательно, зависимость взаимнооднозначная. Известно, что. Отсюда следует, что обратная зависимость также взаимнооднозначная. В этом можно убедиться и непосредственно, вычислив якобиан обратного преобразования

для любого момента времени.

Найдем выражения для скорости и ускорения в лагранжевых переменных. Чтобы выразить скорость, достаточно геометрические координаты заменить на материальные, используя для этого закон движения в лагранжевых переменных. Получим

Найдем ускорение, которое вычисляется как материальная производная скорости. Напомним, что при лагранжевом описании материальная производная совпадает с частной производной по времени.

Пример 2.Дано лагранжево описание движения сплошной среды

Требуется найти его эйлерово описание.

Решение.

Учитывая определение скорости и начальное условие, имеем задачу Коши для системы уравнений:

,

.

Подставим в систему заданное выражение для скорости и проинтегрируем по времени. Получим, проделав несложные выкладки, эйлерово описание:

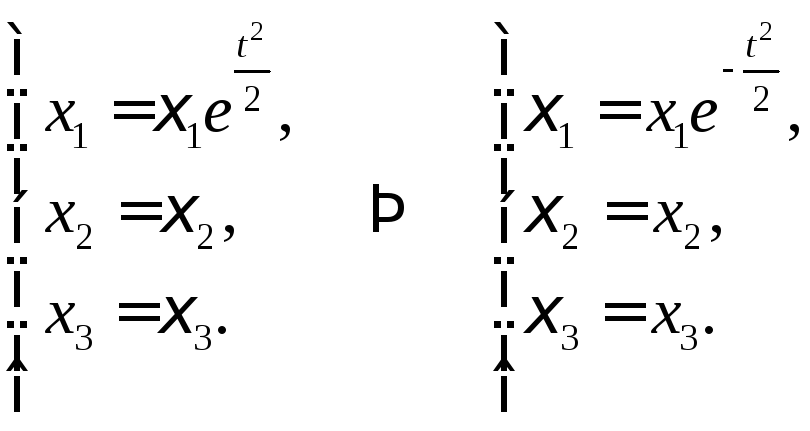
Найдем ускорение, которое вычисляется как материальная производная скорости :

.

Можно вычислить иначе:

,

.

Третий путь состоит в том, чтобы вычислить ускорение в лагранжевых переменных (см. Пример 1), и потом заменить в его выражении материальные координаты на геометрические, как выше было сделано для скорости.

Окончательно: