2. Тензор малых деформаций

Под малыми деформациями понимается движение сплошной среды, при котором длины материальных волокон и углы между ними мало изменяются, то есть относительное удлинение волокон и относительное скашивание первоначально прямых углов между волокнами много меньше единицы. Кроме того, потребуем малость частных производных компонентов перемещений по сравнению с единицей. В этом случае, в выражениях для компонентов тензоров LиEпроизведением малых величин можно пренебречь. Таким образом,линеаризованные тензоры деформацийилитензоры малых деформаций имеют вид:

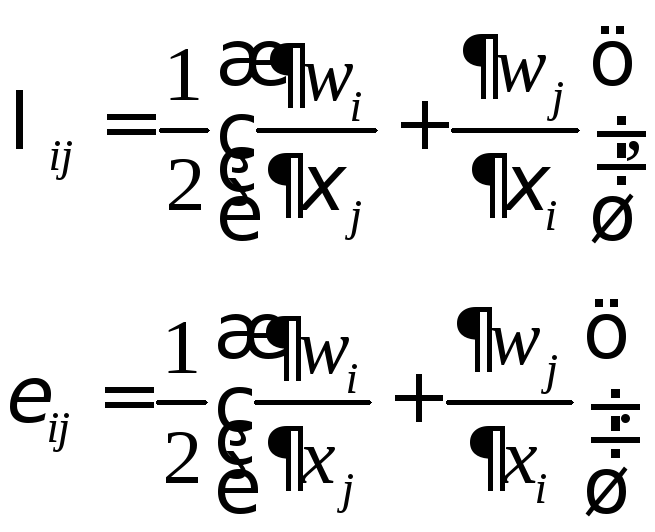
Можно доказать, что тензоры малых деформаций совпадают.

Пример. Пусть движение сплошной среды происходит по закону:

.

Найдем тензор L. Для этого сначала вычислим компоненты вектора перемещений в лагранжевых координатах:

.

Из всех компонентов тензора Lненулевым будет только один –.

.

Найдем тензор E. Сначала вычислим компоненты вектора перемещений в эйлеровых координатах:

.

Тензор Eимеет только один ненулевой компонент:

.

В нашем случае

.

Поэтому нетрудно найти в лагранжевых координатах:

Видно, что . То есть лагранжев и эйлеров тензор конечных деформаций не совпадают.

Найдем лагранжев и эйлеров тензоры малых деформаций и покажем, что они совпадают.

Пусть =. Тогда

,

=.

Вычислим . Так как в линейном приближении

,

то

Итак, .

Перейдем к вычислению относительного изменения длины материального элемента при малых деформациях:

.

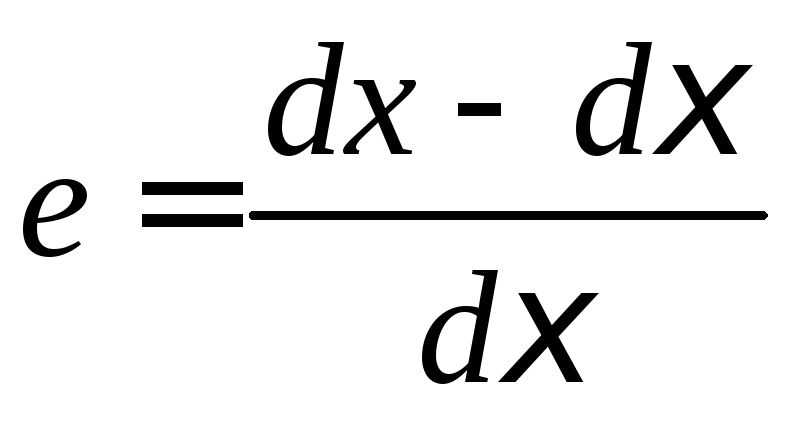Отсюда следует, что

.

В силу малости деформаций относительное изменение длины мало, следовательно, в линейном приближении квадратом этой величины можно пренебречь:

.

Далее

.

Отсюда

.

Относительное изменение длины отрезка выразим через лагранжев или эйлеров тензор малых деформаций, получим:

,.

Можно ввести единичный вектор в направлении рассматриваемого отрезка:

.

Тогда формулу для можно переписать в матричном виде:

,

или

.

3. Механический смысл тензора малых деформаций

Рис.1.5.4

Пусть материальный элемент в момент времени расположен вдоль оси, как показано на Рис.1.5.4. В этом случае,.

Поэтому относительное его удлинение

.

Итак, , то есть относительное удлинение материального элемента, первоначально расположенного вдоль направленияравно компоненте. Точно так же для элементов, первоначально лежащих вдоль осейи, их относительные удлинения равныисоответственно.

Таким образом, диагональная компонента тензора малых деформаций численно равна относительному удлинению вдоль соответствующей оси координат.

Рис. 1.5.5

Рассмотрим деформацию сдвига, т.е. изменение угла между материальными элементами, которые первоначально лежат вдоль двух осей координат. Пусть после деформации отрезокперешел в отрезок,

а отрезок перешел в отрезок(Рис. 1.5.5). Угол между этими векторами, первоначально прямой, перешел в угол. Обозначим изменение этого угла как

.

Тогда .

Разложим перемещение (функцию) в ряд Тейлора в окрестности точки:

,

так как для точки.

Построим векторы ,.

Выразим через перемещение

тогда

.

Аналогично,

.

Вычислим скалярное произведение векторов и:

.

В линейном приближении, в силу малости деформаций:

.

С другой стороны,

в линейном приближении, в силу малости деформаций.

Таким образом,

.

Аналогично можно показать, что ,.

Таким образом, недиагональная компонента тензора малых деформаций численно равна половине изменения первоначально прямого угла между соответствующими осями координат

Замечание.В силу симметричности тензор деформаций имеет три вещественных главных значения, называемые главными деформациями. В любой точке тензор малых деформаций можно привести к главным осям, и он будет иметь диагональный вид, то есть в любой точке существуют три взаимно перпендикулярных волокна, которые при деформации изменяют лишь свою длину, но остаются взаимно перпендикулярными.

Вычислим относительное изменение объема материальной частицы. Для простоты рассмотрим частицу в форме шара. Расположим центр шара в начале координат. В качестве осей координат возьмем главные оси тензора малых деформаций. Вследствие выбора осей координат, при деформации не произойдет скашивания углов, т.е. шар перейдет в эллипсоид.

Вычислим относительное изменение объема .

Пусть радиус шара равен , тогда.

Вычислим объем шара после деформации в линейном приближении относительно :

.

Тогда

,

.

Вычислим первый инвариант тензора малых деформаций через перемещения:

.

Если , то объем шара увеличивается, и наоборот.

Таким образом, первый инвариант тензора малых деформаций – дивергенция вектора перемещения – численно равен относительному изменению малого материального объема сплошной среды.