2. Операции над тензорами

Сложение:T= P+ S.

Умножение тензора на число:T= λ P.

Диадным произведениемдвух векторовTназывается тензор второго ранга с компонентами.

Диадным произведением базисных векторов является тензор второго рангаT, матрица которого имеет один ненулевой элемент.

Полиадным произведениемтензора второго рангаTна векторназывается тензор третьего ранга с компонентами

.

В общем случае, при полиадном произведении ранг произведения равен сумме рангов сомножителей.

Заметим, что диадное и полиадное произведения являются некоммутативными операциями.

Тензор второго ранга, так же, как и вектор, можно разложить по базису, причем базис состоит из девяти тензоров :

T.

Умножение со сверткой. Умножение со сверткой тензоров 1-го ранга представляет собой скалярное произведение, результатом которого является тензор нулевого ранга

.

Умножение со сверткой тензоров 2-го ранга дает в результате скаляр и определяется как

T·S.

Умножение со сверткой тензора 2-го ранга на вектор дает в результате вектор и определяется как

T·.

Заметим, что последняя операция является некоммутативной, т.к.

·T.

Проекцией тензораT на единичный вектор называется вектор, который вычисляется как

TT·.

Заметим, что компонентами проекций тензора на базисные векторы являются соответствующие столбцы матрицы тензора. Например, T– вектор, компоненты которого расположены во 2-м столбце матрицы

Введем определения некоторых тензоров второго ранга специального вида.

Симметричный тензор: .

Антисимметричный тензор: .

Теорема 1.Любой тензор можно представить в виде суммы симметричного и антисимметричного тензоров. Это представление единственно.

◄ Доказательство следует из равенства

.

Единственность доказывается методом от противного. ►

Теорема 2.Симметричный (антисимметричный) тензор при любом ортогональном преобразовании остается симметричным (антисимметричным).

◄ Доказательство. . Аналогично,. ►

Транспонированный тензор:

T^T.

Свойства:

1. если тензор Sсимметричный, тоS^T=S

2. 

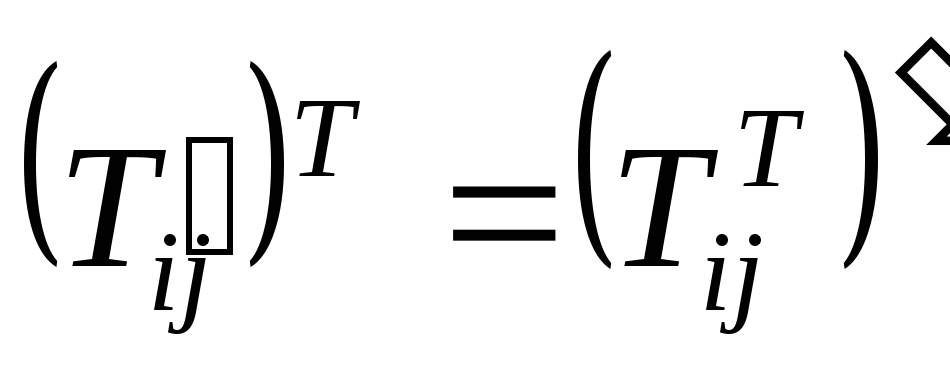
Тензор Кронекера:.

Шаровымназывается тензорS=λ∆.

Изотропнымназывается тензорT, если

.

3. Главные оси и главные значения тензора 2-го ранга

Единичный вектор называетсяглавной осьютензора T, если

T,

т.е. проекция тензора Tна векторколлинеарна. При этом числоназываетсяглавным значениемтензораT.

Из определения главной оси тензора следуют уравнения

,.

или.

В этой системе четыре уравнения и четыре неизвестные: ,, и, т.е. система замкнута.

Первые три уравнения системы являются линейными алгебраическими уравнениями.

С учетом тождества эти уравнения можно переписать в виде

,.

Эта система представляет собой однородную систему линейных алгебраических уравнений относительно неизвестных ,, ее определитель:

.

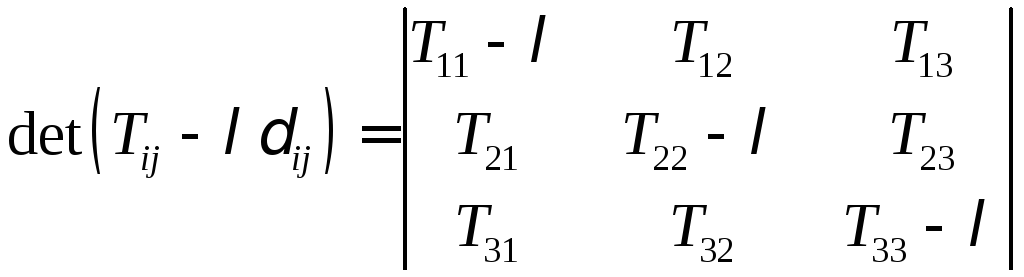Тривиальное решение этой системы (нулевой вектор ,) не представляет интереса, так как нулевой вектор не задает никакого направления.

Ненулевое решение этой системы существует, когда

.

Это равенство представляет собой алгебраическое уравнение относительно главного значения и называетсяхарактеристическим уравнением.

При каждом значении система уравнений

,,

имеет бесконечно много решений. Среди них только два единичных (нормированных) вектора: и.

Преобразуем характеристическое уравнение:

Таким образом, характеристическое уравнение имеет вид:

где

,

,

.

Можно показать, что коэффициенты ,,не меняются при переходе от одной системы координат к другой. Поэтому они называютсяинвариантами тензораT.

Докажем, например, что является инвариантом.

, так как.

Так как коэффициенты характеристического уравнения инвариантны, то и само уравнение, и его решения инвариантны. Таким образом, главные значения тензора инвариантны.

Известно, что у кубического уравнения всегда есть хотя бы один вещественный корень. Нас интересует случай, когда все корни вещественные. Ответ на это вопрос дает следующая теорема.

Теорема (о собственных значениях симметричного тензора). Любой симметричный тензор второго ранга имеет три вещественных главных значения.

◄Доказательство. Пусть– вещественный корень характеристического уравнения тензораT. Тогда можем найти соответствующую главную ось.

Перейдем к новой системе координат. В качестве 1-го базисного вектора штрихованной системы координат выберем единичный вектор :

.

Тогда матрица тензора в новой системе координат примет вид

Так как свойство симметричности тензора является инвариантным, то

.

Запишем характеристическое уравнение в новой системе координат:

.

Преобразуем его:

Отсюда следует квадратное уравнение для нахождения главных значений :

,

Вычислим дискриминант этого уравнения:

Так как дискриминант неотрицательный, то корни вещественные. Теорема доказана. ►

Замечание. Пусть, тогда:

,.

Характеристическое уравнение в этом случае имеет вид

Корни уравнения:

Теорема (о диагональности матрицы тензора). Матрица симметричного тензораTявляется диагональной тогда и только тогда, когда координатный базис составлен из главных осей.

◄ Необходимость.

Пусть матрица тензора Tдиагональна:

.

Найдем проекции тензора на базисные векторы:

T– главная ось тензораT,

T– главная ось тензораT,

T– главная ось тензораT.

Достаточность.

Пусть координатный базис составлен из главных осей, т.е. ,– главные оси тензора. Тогда, по определению главных осей:

T.

Но компоненты Tсоставляютi-й столбец матрицы T, следовательно, матрицаTимеет диагональный вид:

. ►

Следствие. Инварианты симметричного тензораTсвязаны с его главными значениями следующими выражениями:

,

,

.

Теорема (об ортогональности главных осей тензора). Дан симметричный тензор 2-го рангаT.

1. Если и – два неравных между собой собственных значения тензораT, то соответствующие главные оси ортогональны:.

2. Пусть ,– главное значение и главная ось тензораT. Если другие главные значения равны между собой и равны, то любой вектор, ортогональный, является главной осью, соответствующей главному значению:

,T.

◄ 1. По условию теоремы

,,.

Умножим уравнения с нас соответствующим значением, а уравнения снаи сложим все полученные уравнения:

Так как

,

то

.

Тогда

.

Отсюда, в силу , получаем.

2. Из замечания к теореме о собственных значениях следует, что в данном случае и в системе координат, в которой первым базисным вектором является первая главная ось , матрица тензораТимеет вид:

.

Возьмем вектор такой, что. Тогда векторлежит в плоскости,и его можно разложить по базису:

.

Найдем проекцию:

ТТТТТ

Следовательно, – главная ось. ►

Следствие.

1. Пусть . В этом случае тензорТимеет видТ, то есть является шаровым, и любой единичный вектор является главной осью:

Т.

2. . Трем различным собственным значениям соответствуют три взаимно ортогональные главные оси, причем эта тройка векторов единственна (с точностью до знака).

3. Других случаев нет.