§ 6. Построение циркулем и линейкой в древней Греции

В V в. до н.э. циркуль и линейка выделились как основные инструменты геометрических построений. Довольно быстро греки научились решать основные задачи на построение: деление отрезка на равные части, построение угла, равного данному, и др. Но здесь впервые встретились задачи, которые не поддавались решению, несмотря на то, что объект, который требовалось построить, существует. Это были получившие широкую известность задачи об удвоении куба, о трисекции угла и о квадратуре круга.

1.Задача об удвоении куба заключается в построении куба, объем которого вдвое больше объема данного куба. Если обозначить длину ребра данного куба через , а искомого – через , то задача эквивалентна построению корня уравнения

(1)

Эта задача была настолько популярной, что о ее происхождении греки сочинили легенду. Рассказывали, что на острове Делос вспыхнула эпидемия чумы. Когда граждане спросили оракула, как избавиться от этого бедствия, он ответил, что нужно удвоить жертвенник, имевший форму куба, не меняя его формы. В связи с легендой задача получила название делосской. В действительности же задача возникла в результате развития геометрических построений. Еще пифагорейцы знали, что квадратичные иррациональности можно построить циркулем и линейкой. Естественно было теперь перейти к кубическим иррациональностям. Простейшей из них и была иррациональность

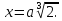
Гиппократ Хиосский, греческий ученый V в. до н.э., установил, что для построения корня уравнения (1) достаточно построить два отрезка 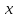и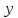, средних пропорциональных к отрезкам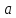и, т.е. таких, что

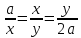, (2)

В самом деле, исключим 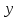из пропорций

.

Получим:

,

,

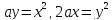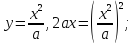
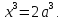
Менехм, ученый IV в. до н.э., ввел в математику конические сечения (т.е. кривые второго порядка), главным образом, для решения задачи об удвоении куба. Для этого достаточно было найти точку пересечения параболы 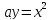и гиперболы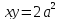; отрезок является, по предыдущему, искомым.

У греков существовал также прибор –«уловитель средних», с помощью которого находили отрезк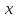и и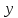, удовлетворяющие условию(2).

Уже в конце IVв. д. н. э. ученые древней Греции догадывались, что задача об удвоении куба неразрешима циркулем и линейкой. Но лишь в XVII в. н. э. французский ученый Р.Декарт сформулировал теорему: корни кубического уравнения с целыми коэффициентами можно построить циркулем и линейкой тогда и только тогда, когда это уравнение имеет рациональный корень. Впрочем, теорема была доказана значительно позже, в 1837г. французским математиком П. Вантцелем.

Поскольку уравнение (1) при рациональном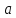имеет единственный действительный корень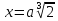и он рационален, так как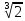есть число иррациональное, то корень нельзя построить циркулем и линейкой.

2.Задача о трисекции угла состоит в делении данного угла на три равные части. Она также возникла из практики геометрических построений: после того, как был найден способ деления на 2, а следовательно, и на 4, 8, 16 и т.д. равных частей циркулем и линейкой, естественно было перейти к делению угла на иное число равных частей. Наименьшим таким числом является 3.

В средине века ученые арабских стран установили, что решение и этой задачи сводится к построению корня кубического уравнения. в самом деле, построение угла равносильно построению его синуса. Поэтому. если положить данный угол, и воспользоваться формулой синуса тройного угла

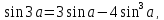
то получим:

,

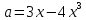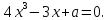
Теперь применим теорему Декарта о кубическом уравнении. Предварительно умножим обе части последнего уравнения на 2 и в новом уравнении положим 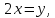с тем,чтобы сделать уравнение приведенным:

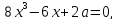
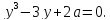(3)

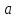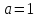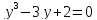Кубическое уравнение (3) при некоторых рациональных значениях имеет рациональный корень. Так будет, например, при : уравнениеимеет рациональный корень, а следовательно, синусу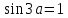соответствует угол, который можно разделить на три равные части циркулем и линейкой. но так будет не всегда: например, при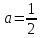получим уравнение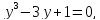которое не имеет рациональных корней, так как все рациональные корни приведенного уравнения, если они существуют, являются целыми числами и, кроме того, находятся среди делителей свободного члена уравнения, т.е. в данном случае среди чисел ±1, однако эти числа корнями уравнения не являются.

Таким образом, задача о трисекции угла в общем случае неразрешима циркулем и линейкой. Следовательно, эту задачу, как и задачу об удвоении куба, можно решить только неэлементарными методами.

ВV в. до н. э. для решения задачи о трисекции угла Гиппий из Элиды изобрел новую кривую, позднее названную квадратрисой. Квадратриса определялась с помощью механики.

Пусть в квадрате 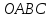стороны 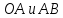начинают одновременно двигаться. причем отрезок 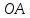вращается по часовой стрелке вокруг точкиО с постоянной угловой скоростью ω до совпадения с ОС, а отрезок АВ перемещается вниз с постоянной линейной скоростью V,оставаясь параллельным своему начальному положению, до совпадения с ОС . Пусть при этом отрезки ОА и АВ достигают положения ОС одновременно. Множество точек М пересечения отрезков 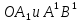, соответствующих одному и тому же моменту движения. и называется квадратрисой (рис.8).Начальная точка квадратрисы есть точка А, конечная же точка К. лежащая на отрезке ОС, квадратрисе, очевидно, не принадлежит.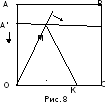

Возьмем два момента движения отрезок ОА повернется на угол ∠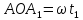, а к моменту 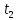- на угол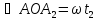. ОтрезокAB к моменту 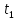проделает путь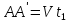, а к моменту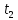-путь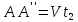.Отсюда

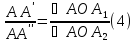
поскольку каждое из этих отношений равно .

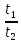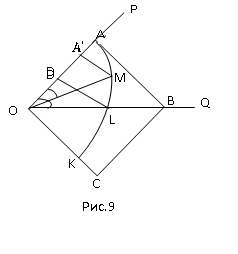
Из пропорций (4) вытекает следующий способ деления данного острого угла 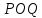на три равные части. Строим квадратOABC ,одна из вершин которого совпадает с вершиной О угла, а сторона OA лежит на одной из сторон OP угла Рис.9 Из вершины A квадрата проведем квадратрису, обозначим через L точку ее пересечения с прямой OQ и проведем через L прямую LD параллельно прямой AB, где D- точка пересечения этой прямой с отрезком ОА. На стороне OA квадрата от точки 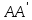отложим отрезок такой, что 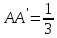AD , и проведем через точку 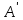прямую, параллельную прямойАВ и пересекающую квадратрису в точке 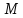. Так как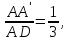то на основании пропорции (4)т.е. угол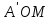 cоставляет третью часть угла POQ.

Из решения видно, что квадратриса является универсальной кривой: с ее помощью можно делить данный угол на любое число равных частей.

Несколько решений задачи о трисекции угла было получено так называемым методом вставки. Название объясняется тем, что данный отрезок, отмеченный на линейке, с помощью линейки вставляется между двумя данными линиями, например, между прямой и окружностью. Хотя при этом в большинстве случаев использовались только циркуль и линейка, само решение нельзя считать элементарным, поскольку линейкой выполнялось иное построение, чем обычно.

3.Задача о квадратуре круга состоит в построении квадрата, равновеликого данному кругу. ВV в. до н. э. греческие ученые научились циркулем и линейкой преобразовывать многоугольник в равновеликий треугольник, а треугольник- в равновеликий квадрат. Естественно было теперь перейти к криволинейным фигурам. Простейшей из них был круг.

Если обозначить радиус данного круга через R , а сторону равновеликого квадрата через 𝓍, то получим уравнение

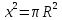(5)

Задача о построении корня этого уравнения циркулем и линейкой сводится к вопросу: можно ли построить циркулем и линейкой отрезок длины π? Лишь в семидесятые годы XIX в. н. э. немецкий ученный Ф. Линдеман доказал, что число π трансцендентно, т. е. является корнем никакого алгебраического уравнения с рациональными коэффициентами. Отсюда вытекает, что задача о квадратуре круга неразрешима циркулем и линейкой, поскольку циркулем и линейкой можно построить только такой отрезок, длина которого есть число алгебраическое, т. е. корень алгебраического уравнения с рациональными коэффициентами, да и для алгебраических чисел не всегда возможно это сделать (например, это возможно для корня уравнения

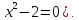
Динострат (IV в. до н. э.) решил задачу с помощью квадратрисы. С этой целью выведем ее уравнение.

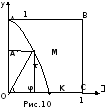
В прямоугольной декартовой системе координат построим единичный квадрат 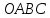, у которого две соседние стороны лежат на осях координат

(рис. 10). Проведем через вершину A квадрата квадратрису. Пусть сторона AB при ее параллельном перемещении вниз и сторона OA при ее вращении вокруг точки О достигают положения ОС за единицу времени.

Выберем момент t движения сторон АВ и ОА квадрата, где 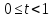, и обозначим соответствующую точку квадратрисы через М. Пусть y – ордината точки, 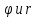– ее полярные координаты.

Поскольку длина стороны квадрата равна 1, то линейная скорость перемещения стороны АВ есть 𝒱 = 1, а угловая скорость вращения стороны .

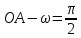Тогда ,

, .

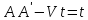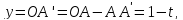
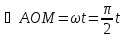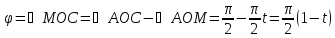Дале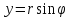е,, т.е..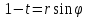

Исключим параметр t из образовавшейся системы уравнений

Будем иметь:

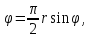
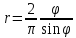. (6)

Уравнение (6) является уравнением квадратрисы в полярных координатах. Хотя ученые древней Греции не знали алгебраической символики и тригонометрических функций, они умели читать уравнение квадратрисы словесно, в довольно громоздкой формулировке.

Найдем длину отрезка ОК, т.е. полярный радиус точки К. Эта точка не принадлежит квадратрисе, поэтому ее полярный радиус можно найти только с помощью предельного перехода. Древние греки не знали теории пределов, однако знали ряд предложений, эквивалентных некоторым теоремам о пределах, в частности, предложение, эквивалентное соотношению 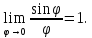Поэтому мы, осовременивая и сокращая их доказательство, применим предельный переход:

.

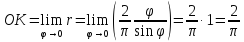Зная отрезок ОК, теперь легко построить отрезок длины π , а следовательно, решить задачу о квадратуре круга.

Рассмотренные здесь геометрические задачи сыграли значительную роль в истории математики. Главное – они поставили вопрос о критерии разрешимости задач на построение с помощью циркуля и линейки. Они стимулировали развитее ряда вопросов современной математики: о разрешимости алгебраических уравнений в квадратных радикалах, о природе числа π и др. Для решения этих задач были изобретены специальные кривые: парабола, гипербола, квадратриса и др., которые оказались необходимыми в нескольких областях математики.