§ 39. Создание дифференциальной и проективной геометрии

1.Дифференциальная геометрия возникла в XVIII в. из приложений дифференциального и интегрального исчисления к аналитической геометрии. Первые задачи подобного рода были решены еще в XVII в. в рамках дифференциального исчисления; это были задачи на касательную, на кривизну плоской кривой, на огибающую семейства кривых и др.

Рассмотрим здесь понятие кривизны. Пусть есть дуга кривой. Проведем к ней касательные в точках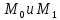(рис.45). Пусть длина этой дуги равна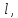а угол между касательными

−

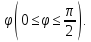
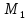
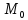
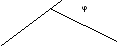
Отношение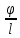называется средней

кривизной кривой; оно выражает угол пово-

Рис.45

рота касательной, приходящийся в среднем

на единицу длины дуги. Говоря современным языком предел

средней кривизны, когда точка 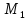неограниченно приближается по кривой к точке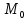, называется кривизной кривой в точке: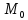

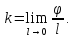
В частности, для окружности получаем:

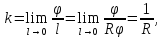
т.е. кривизна окружности постоянна и обратна ее радиусу.

В 1731 г. А.К. Клеро в работе «Исследование о кривых двоякой кривизны» рассмотрел кривизну пространственной кривой. Термин «двоякая кривизна кривой», используемый и сейчас, объясняется тем, что пространственная кривая у Клеро определялась своими ортогональными проекциями на две взаимно перпендикулярные плоскости.

Несколько работ, посвященных дифференциальной геометрии, написал Эйлер. При этом он рассматривал, в основном, поверхности. В частности, Эйлер исследовал геодезические линии на поверхностях, т.е. кривые, соединяющие две данные точки поверхности, лежащие на ней и имеющие наименьшую длину; например, на сфере геодезической линией является меньшая из двух дуг большой окружности сферы, проходящей через эти точки. Изучая геодезические линии на цилиндрической и конической поверхностях, он пользовался тем, что при развертывании этих поверхностей на плоскость геодезические линии превращаются в отрезки прямых. Эйлер исследовал также развертывающиеся поверхности, т.е. поверхности, которые могут быть наложены на плоскость без складок и разрывов, и нашел все такие поверхности: цилиндрические, конические и поверхности образованные касательными к пространственным кривым.

Важную роль в развитии дифференциальной геометрии сыграл Монж. Гаспар Монж (1746−1818), выходец из крестьянско-буржуазной семьи, стал в 1780 г. членом Парижской академии наук, был одним из основателей Политехнической школы и ее профессором. Являлся активным деятелем Французской буржуазной революции. Во времена Наполеона был морским министром и организатором военной промышленности Франции. В математике занимался дифференциальной и начертательной геометрией.

В начертательной геометрии Монж был основоположником. Она возникла из технических приложений математики, а также из законов перспективы, которыми пользуются художники и архитекторы. В 1798−1799гг. Монж опубликовал курс начертательной геометрии «Геометрия перспективы». В этом сочинении он систематически провел отображения пространственных тел на две взаимно перпендикулярные координатные плоскости, а пространственные перемещения и построения свел к соответствующим преобразованиям проекций. Сейчас начертательная геометрия является теоретической основой технического черчения.

Дифференциальной геометрии посвящено сочинение Монжа с характерным названием «Приложение анализа к геометрии», изданное в 1807 г. В нем он дал систематическое изложение теории поверхностей. По мнению Монжа, классификацию поверхностей, с точки зрения приложений и нужд технического образования, лучше проводить не по виду их алгебраических уравнений, а, с помощью перемещения в пространстве некоторой линии, по виду поверхности, заданные дифференциальными уравнениями первого и второго порядка. В частности, для цилиндрических и конических поверхностей получаются дифференциальные уравнения первого порядка.

В XIX в. начинается новый этап развития дифференциальной геометрии – разработка внутренней геометрии поверхностей. Здесь главным является вклад Гаусса. В 1828 г. он напечатал работу «Общие исследования о кривых поверхностях».

В ней автор пользуется, главным образом, параметрическими уравнениями поверхности

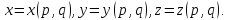
Если одному из параметров, например, придать фиксированное значение, то уравнения превратятся в параметрические уравнения пространственной кривой с параметром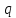; если же зафиксировать значението получатся параметрические уравнения кривой с параметромОбразуется два семейства кривых, составляющие криволинейную параметрическую сеть. Она является координатной сетью в той области поверхности, где через каждую точкупроходит только одна кривая каждого семейства и любые две кривые, взятые из различных семейств, пересекаются не более чем в одной точке. Такая система координатназывается криволинейными (гауссовыми) координатами; эти координаты вводятся по образцу широт и долгот на сфере. Саму поверхность по отношению к криволинейным координатамможно считать двумерной.

Гаусс вводит отображение области поверхности на область единичной сферы с помощью нормалей. Теперь он определяет так называемую гауссову кривизну поверхности в точке как предел отношения площади области на сфере к площади соответствующей области поверхности, когда последняя стягивается в эту точку. Гаусс доказывает важное предложение: если поверхность можно развернуть на любую другую поверхность без складок и разрывов, с сохранением длин кривых, то кривизна поверхности не меняется. Свойства, сохраняющиеся при всевозможных непрерывных изгибаниях поверхности, Образуют внутреннюю геометрию поверхностей. К ним, в частности, относятся гауссова кривизна поверхности, свойство линии на поверхности быть геодезической и др. При исследовании поверхностей Гаусс широко использует дифференциальную геометрию; в частности, он часто применяет две квадратичные дифференциальные формы (возможно, известные читателю из вузовского курса геометрии).

После Гаусса значительный вклад в разработку внутренней геометрии поверхностей внесли Ф.Г. Миндинг, К.Г. Якоби, Д. Лиувилль, К.М. Петерсон и др.

2.Перейдем к истории проективной геометрии.

Некоторые проективные методы встречаются в работах древнегреческих математиков Аполлония, Паппа и др. В XVII в. две теоремы проективной геометрии доказали Ж. Дезарг и Э. Паскаль, но соответствующие работы обоих были напечатаны очень малым тиражом, поэтому их заметили лишь немногие ученые и они не получили дальнейшего развития. Метод проектирования возродился на рубеже XVIII и XIX веков в работах Г. Монжа в связи с его занятием начертательной геометрией, а также в работах некоторых его учеников: Л. Карно, Ш. Брианшона и др.

Проективная геометрия как самостоятельная область геометрии – наука о проективных свойствах фигур – с систематическим изложением основных ее понятий и теорем впервые выступила у Понселе.

Французский ученый Жан Виктор Понселе (1788−1867) учился в политехнической школе, был военным инженером. Его интерес к вопросам проектной геометрии, видимо, объясняется влиянием Монжа, лекции которого он слушал, и работ Карно. Участвовал в походе Наполеона в Россию, попал в плен. Два года провел в Саратове, что дало ему возможность оформить свои идеи, относящиеся к проективной геометрии. По возвращении во Францию работал профессором Прикладной школы в Меце, позднее переехал в Париж, где стал профессором в Сорбонне и начальником Политехнической школы.

В 1822 г. в Париже Понселе издал «Трактат о проективных свойствах фигур»; от названия этого сочинения родился термин «проективная геометрия».

Понселе задался вопросом: какие свойства сохраняются при центральном проектировании? Оказалось, что точки, лежащие на одной прямой, проектируются в точки, лежащие на одной прямой; пересекающиеся (параллельные) прямые проектируются в пересекающиеся (параллельные) прямые; сохраняется и отношение двух отрезков, лежащих на одной прямой (рис. 46):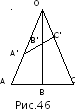

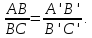
Он называл свойства ( или отношения), которые выполняются одновременно и у фигуры, и у ее проекции, проективными. В работе Понселе впервые на передний план выступила идея геометрических преобразований, которая до тех пор мало применялась в математике.

Понселе вводит важное для дальнейшего понятие двойного отношения: двойным (или сложным отношением четыре точек лежащих на одной прямой, называется число, равное

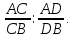
При этом двойное отношение считается положительным, если направления отрезков 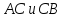совпадают, и отрицательным в противном случае.

Двойное отношение четырех точек также является проективным, так как каждое из отношений 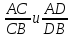сохраняется.

Понселе пополняет прямую бесконечно удаленной точкой, а плоскость − бесконечно удаленной прямой. При этом соглашении любые две прямые на плоскости пересекаются, любые две плоскости в пространстве пересекаются.

Понселе сформулировал важный принцип двойственности: если верно какое-либо предложение, касающееся точек, прямых и отношения инцидентности (принадлежности) между ними, то верно и так называемое двойственное предложение, которое получается из данного, если поменять местами слова «точка» и «прямая». Например, для предложения: « Двум различным прямым инцидентна точка и притом только одна» двойственным является предложение: « Двум различным точкам инцидентна прямая и притом только одна». Этот принцип отражает фундаментальное свойство проективной плоскости: прямые и точки на ней являются совершенно равноправными геометрическими объектами.

Работу Понселе продолжила группа немецких геометров: А.Ф. Мебиус, Я. Штейнер, Ю. Плюккер, Х. Штаудт и др., а также французский ученый М. Шаль и английский А. Кэли. Мебиус и Плюккер ввели в проективную геометрию аналитические методы. Так, Плюккер стал рассматривать однородные координаты (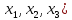точки проективной плоскости, гдене равны одновременно нулю, а уравнение бесконечно удаленной прямой записал в виде. 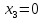Конечные точки евклидовой плоскости он задал обычными координатами, выражающимися через однородные координаты формулами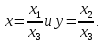

Так как ряд понятий проективной геометрии долгое время вводился с помощью длины отрезка, то она не имела собственной основы. Только Штаудт дал проективной геометрии основу, независимую от метрики, в работе «Геометрия положения» (1847). Например, двойное отношение четырех точек он впервые определяет чисто проективным путем. Детали такого изложения проективной геометрии здесь не рассматриваются; укажем лишь, что Штаудт при выполнении построений на плоскости вынужден был ограничится теми построениями, которые выполняются одной линейкой.