
- •Предисловие
- •Введение
- •§ 1. Предмет математики и истории математики
- •§ 2 Основные периоды развития математики
- •§ 3. Математика древнего Египта
- •§ 4. Математика древнего Вавилона
- •§5. Начало древнегреческой математики
- •§ 6. Построение циркулем и линейкой в древней Греции
- •§ 7. Парадоксы Зенона
- •§ 8. Предшественники Евклида
- •§ 9. Общая характеристика “Начал” Евклида
- •§10. Геометрические книги “Начал”.
- •§ 11. Арифметические книги “Начал”
- •§ 12. Архимед. Работа Архимеда “ Измерение круга”
- •§13. Работа Архимеда “ o спиралях”
- •§14 Создание теории конических сечений
- •§15. Древнегреческая математика после Аполлония
- •Возникновение алгебры и теории чисел
- •Греческая математика после Диофанта
- •Математика древнего и средневекового Китая
- •§ 17. Математика древней и средневековой Индии
- •§ 18. Математика в арабских странах
- •§ 19. Математика в Западной Европе в X XIV вв.
- •§ 20. Древнерусская математика
- •§ 21. Создание алгебраической символики
- •§ 22. Решение уравнений третьей и четвертой степени
- •§ 23. Развитие тригонометрии в XII-XVII вв.
- •§ 24. Составление таблиц логарифмов
- •1,0001:
- •§ 25. Создание основ аналитической геометрии
- •§ 26. Первые предшественники интегрального исчисления
- •§ 27. Последующие предшественники интегрального исчисления
- •§ 28. Предшественники дифференциального исчисления
- •§ 29. Дифференциальное исчисление у Ньютона
- •§ 30. Интегральное исчисление у Ньютона
- •§ 31. Дифференциальное исчисление у Лейбница
- •§ 32. Интегральное исчисление у Лейбница
- •§ 33. « Арифметика» Магницкого
- •§34. Математический анализ в XVIII веке
- •§ 35. Учение о числе в XVII – XIX вв.
- •§ 36. Математический анализ в XIX веке
- •§ 37. Алгебра в XVIII – XIX вв.
- •§ 38. Теория чисел в XVII−XIX вв.
- •§ 39. Создание дифференциальной и проективной геометрии
- •§ 40. Создание неевклидовой и многомерной геометрии. Аксиоматизация геометрии
- •§ 41 Проблемы Гильберта
- •§ 42. Ведущие области математики XX веке
- •Заключение
- •Литература
- •§ 1. Предмет математики и история математики……………………….. 5
§ 38. Теория чисел в XVII−XIX вв.
ВXVII в. ведущей фигурой в теории чисел был П. Ферма.
Он
искал такие выражения
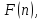 которые при любом натуральном
которые при любом натуральном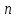 принимали бы только простые значения.
Ферма полагал, что таким выражением
является
принимали бы только простые значения.
Ферма полагал, что таким выражением
является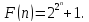 При
При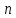 =
0,1,2,3,4 последнее выражение действительно
принимает значения, являющиеся простыми
числами. Но позднее Эйлер установил,
что уже
=
0,1,2,3,4 последнее выражение действительно
принимает значения, являющиеся простыми
числами. Но позднее Эйлер установил,
что уже не простое. ВXVIII
в. Хр. Гольдбах и Эйлер доказали, что не
существует многочлена
не простое. ВXVIII
в. Хр. Гольдбах и Эйлер доказали, что не
существует многочлена
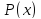 с целыми коэффициентами, который при
всех натуральных
с целыми коэффициентами, который при
всех натуральных принимал бы только простые значения.
принимал бы только простые значения.
Ферма
сформулировал теорему: если
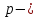 простое число, то при любом натуральном
простое число, то при любом натуральном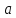 разность
разность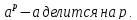 Эта малая теорема Ферма – одна из самых
важных теорем элементарной теории
чисел.
Эта малая теорема Ферма – одна из самых
важных теорем элементарной теории
чисел.
Много
внимая он уделял решению неопределенных
уравнений в целых числах. Еще до Ферма
было решено уравнение первой степени
с двумя неизвестными. Ферма, по-видимому,
решил уравнение второй степени
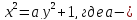 натуральное число, не являющееся точным
квадратом, − так называемое уравнение
Пелля. Ферма сформулировал теорему:
уравнение
натуральное число, не являющееся точным
квадратом, − так называемое уравнение
Пелля. Ферма сформулировал теорему:
уравнение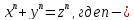 натуральное число, большее 2, неразрешимо
в натуральных числах
натуральное число, большее 2, неразрешимо
в натуральных числах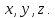 Эта теорема позднее получила название
большой, или великой теоремы Ферма. Сам
Ферма доказал ее при
Эта теорема позднее получила название
большой, или великой теоремы Ферма. Сам
Ферма доказал ее при возможно, при
возможно, при У этой теоремы оказалась интригующая
история. Многие математикиXVIII−XX
вв. пытались ее доказать, но, в лучшем
случае. давали доказательство лишь для
отдельных значении
У этой теоремы оказалась интригующая
история. Многие математикиXVIII−XX
вв. пытались ее доказать, но, в лучшем
случае. давали доказательство лишь для
отдельных значении
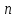 или
для отдельных классов значений
или
для отдельных классов значений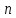 . Мало того, теорему пытались доказать
и тысячи любителей математики из разных
стран, исходя, видимо, из убеждения, что
если теорема просто формулируется. то
она и просто доказывается. Но орешек
оказался весьма твердым. Проблема была
решена в самом концеXX
в. Американский математик Э.Уайлс, весьма
существенно использовав ЭВМ, сумел дать
полное доказательство теоремы.
. Мало того, теорему пытались доказать
и тысячи любителей математики из разных
стран, исходя, видимо, из убеждения, что
если теорема просто формулируется. то
она и просто доказывается. Но орешек
оказался весьма твердым. Проблема была
решена в самом концеXX
в. Американский математик Э.Уайлс, весьма
существенно использовав ЭВМ, сумел дать
полное доказательство теоремы.
Нужно сказать, что Ферма свои научные работы почти не публиковал, они становились известными, главным образом, из переписки. Почти все свои теоремы он приводил без доказательств.
2.Основания теории чисел заложил в XVIII в. Л. Эйлер. Ему принадлежит свыше ста, небольших по объему, работ по теории чисел, а кроме того, вопросам теории чисел посвящены отдельные главы во «Введении в анализ бесконечных» и некоторые разделы в «универсальной арифметике».
Ряд
проблем теории чисел он заимствовал у
Ферма. Эйлер доказал малую теорему Ферма
и так называемую теорему Эйлера,
являющуюся ее общением: если натуральные
числа
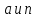 взаимно просты, то разность
взаимно просты, то разность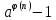 делится на
делится на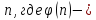 функция Эйлера, выражающая количество
натуральных чисел, меньших
функция Эйлера, выражающая количество
натуральных чисел, меньших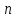 и взаимно простых с
и взаимно простых с .
Он доказал утверждение Ферма, что любое
простое число вида
.
Он доказал утверждение Ферма, что любое
простое число вида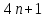 можно представить в виде суммы двух
точных квадратов и притом единственным
образом. Эйлер решил в целых числах
уравнение Пелля
можно представить в виде суммы двух
точных квадратов и притом единственным
образом. Эйлер решил в целых числах
уравнение Пелля свел любое неопределенное уравнение
второй степени с двумя неизвестными и
с целыми коэффициентами к уравнению
Пелля с помощью подстановок.
свел любое неопределенное уравнение
второй степени с двумя неизвестными и
с целыми коэффициентами к уравнению
Пелля с помощью подстановок.
Эйлер положил начало аналитической теории чисел. Он применил методы математического анализа, главным образом, бесконечные ряды и произведения, к задачам о представлении натуральных чисел в виде суммы или произведения натуральных чисел определенного вида.
Теорией чисел в XVIII в. занимались еще Ж.Л. Лагранж, А.М. Лежандр и др.
3.В XIX в. теория чисел существенно меняет свой характер. Это связано прежде всего с именем Гаусса.
Карл
Фридрих Гаусс (1777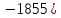 родился в Германии в Брауншвейге в
семье водопроводчика. Уже в начальной
школе обратил на себя внимание учителя,
когда в уме быстро вычислил сумму
родился в Германии в Брауншвейге в
семье водопроводчика. Уже в начальной
школе обратил на себя внимание учителя,
когда в уме быстро вычислил сумму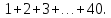 В 1795−1797 гг. учился в университете в
Геттингене. Работал сначала приват-доцентом
университета в Брауншвейге, а с 1807 г. до
конца жизни − профессором в и директором
местной астрономической обсерватории.
В 1795−1797 гг. учился в университете в
Геттингене. Работал сначала приват-доцентом
университета в Брауншвейге, а с 1807 г. до
конца жизни − профессором в и директором
местной астрономической обсерватории.
Перечислим некоторые первые его научные работы. В возрасте 18 лет он изобрел метод наименьших квадратов – один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки. Этот метод имел прикладное значение и вскоре стал применяться. в том числе и самим Гауссом. для обработки результатов астрономических и геодезических наблюдений. В возрасте 19 лет он нашел способ построения правильного 17-угольника с помощью циркуля и линейки. В 1799г. он получил степень доктора за диссертацию, посвященную доказательству основной теоремы алгебры. В 1801г. Гаусс издал большую работу « Арифметические исследования» − сочинение, посвященное теории чисел и явившееся поворотным пунктом в развитии этой науки.
Гаусс был разносторонним учеником. Он работал почти во всех областях математики того времени: в алгебре, теории чисел, дифференциальной и проективной геометрии, математическом анализе, теории функций комплексной переменной, теории вероятностей, а также в астрономии, геодезии, механике и теории магнетизма. Он органически соединял теоретические и прикладные исследования. Особое значение Гаусс придавал теории чисел; он говорил: «Математика − царица наук, арифметика − царица математики». В двадцатые годы XIX в. Гаусс считался первым среди математиков – королем математики. Однако он печатал сравнительно мало работ; многие важные открытия были обнаружены в его бумагах после смерти.
Остановимся подробнее на содержании работы «Арифметические исследования».
Гаусс вводит понятие сравнения. Сравнения фактически уже встречались в работах некоторых его предшественников, но он ввел это понятие в явном виде и построил стройную теорию сравнений, которая играет в теории чисел роль, сходную с ролью теории уравнений в алгебре.
Два
целых числа
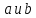 Гаусс называет сравнимыми по модулю
Гаусс называет сравнимыми по модулю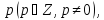 если разность
если разность Символическое обозначение:
Символическое обозначение: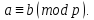 Каждое из чисел
Каждое из чисел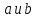 в этом случае называется вычетом другого
по модулю
в этом случае называется вычетом другого
по модулю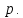
Теорию сравнения Гаусс строит по аналогии с теорией алгебраических уравнений. Сначала он рассматривает сравнения первой степени
 затем
– сравнения
затем
– сравнения
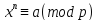 и излагает теорию степенных вычетов,
наконец, весьма подробно изучает
сравнения второй степени
и излагает теорию степенных вычетов,
наконец, весьма подробно изучает
сравнения второй степени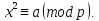 Гаусс доказывает, что
Гаусс доказывает, что имеет не более
имеет не более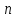 корней, вводит в неявном виде понятие
первообразного корня по любому простому
модулю
корней, вводит в неявном виде понятие
первообразного корня по любому простому
модулю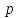 ,
т.е. такого целого числа
,
т.е. такого целого числа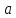 ,
что сравнение
,
что сравнение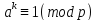 имеет место при
имеет место при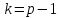 (в соответствии с малой теоремой Ферма),
но не выполняется при
(в соответствии с малой теоремой Ферма),
но не выполняется при и доказывает его существование.
и доказывает его существование.
Ведущее
место в книге Гаусса занимает теория
квадратичных форм. Он подробно изложил
ее для форм от двух переменных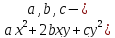 целые). Одна из задач, которую он решает,
− нахождение множества целых чисел
целые). Одна из задач, которую он решает,
− нахождение множества целых чисел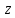 представимых данной формой, например,
суммой или разностью двух точных
квадратов.
представимых данной формой, например,
суммой или разностью двух точных
квадратов.
Позднее
в другой работе («Теория биквадратичных
вычетов») Гаусс ввел целые комплексные
числа – выражения вида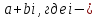 мнимая единица,
мнимая единица,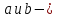 обычные целые числа. Он строит теорию
таких чисел по аналогии с теорией целых
чисел: вводит простые и составные числа,
алгоритм Евклида, доказывает, что каждое
целое комплексное число разлагается
на простые множители однозначно, строит
для новых чисел теорию степенных вычетов
и т.д. Например, в этой новой области
число
обычные целые числа. Он строит теорию
таких чисел по аналогии с теорией целых
чисел: вводит простые и составные числа,
алгоритм Евклида, доказывает, что каждое
целое комплексное число разлагается
на простые множители однозначно, строит
для новых чисел теорию степенных вычетов
и т.д. Например, в этой новой области
число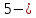 составное, так как
составное, так как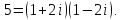 Главное же – Гаусс и некоторые его
последователи применили целые комплексные
числа к решению ряда задач теории чисел.
Главное же – Гаусс и некоторые его
последователи применили целые комплексные
числа к решению ряда задач теории чисел.
В XIX в. существенные результаты в теории чисел получили еще К. Якоби, П. Дирихле, П.Л. Чебышев и др.
