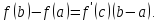§34. Математический анализ в XVIII веке

XVIII век был в Западной Европе веком дальнейшего укрепления буржуазного строя, веком технической революции ( изобретение паровой машины). Одновременно он был веком просвещения, веком повсеместного распространения образования.

Весьма важным событием в истории Европы была Французская буржуазная революция, произошедшая в 1789 г. Идеологической подготовкой этой революции была деятельность французских просветителей и философов Вольтера, Руссо и др., а также издание Д.Дидро и Ж. Даламбером « Энциклопедии» (28 томов), проникнутой демократическим и материалистическим духом.

Центрами развития науки являются академии наук; ведущими среди них были Парижская, Берлинская и Петербургская. Резко увеличивается выпуск периодической научной литературы.

Среди естественных наук ведущее место занимает механика, которая в XVIII в. широка применяет аппарат математического анализа. Математический анализ играет главную роль в математике. Его методы проникают в геометрию, алгебру, теорию чисел, теорию вероятности. Если в XVII в. математический анализ состоял из дифференциального и интегрального исчисления, то теперь в нем складываются новые крупные составные части: функции многих переменных, теория дифференциальных уравнений (обыкновенных и в частных производных), дифференциальная геометрия, теория рядов, вариационное исчисление.

XVIII в. дал в математическом анализе колоссального много нового фактического материала. Гораздо хуже обстояло дело с основными понятиями, с обоснованием полученных результатов. XVIII в. сотрясали споры ученых по этим вопросам.

Одним из предметов споров было выяснение понятия функции. Термин «функция» ввел еще Лейбниц в XVII в. для обозначения переменных отрезков, связанных с кривой. В XVIII в. ученые широко применяли этот термин, понимая под функцией величину, зависящую от другой величины ( или от нескольких величин). Но само это последнее понятие страдало неопределенностью и требовало уточнения. Спор шел, в частности, о том, можно ли отождествить функцию с формулой? И. Бернулли и Л. Эйлер считали: да, можно. Однако тот же Эйлер позднее стал на более общую точку зрения, отождествляя функцию с произвольно начертанной кривой. Окончательное решение вопроса о понятии функции было достигнуто лишь в XIX в.

Другая, более важная тема для споров ученых XVIII в.: что такое бесконечно малая? Как построить анализ бесконечно малых строго логически? Эйлер считал, что бесконечно малая есть нуль, а исчисление бесконечно малых есть исчисление своего рода нулей. Лишь в конце XVIII – начале XIX в. стало приходить понимание того, что бесконечно малая является не постоянной, как считали многие ученые XVIII в., а переменной с особым характером изменения. Даламбер в «Энциклопедии» в статье «Предел» дал определение предела переменной: «Говорят, что одна величина является пределом другой величины, если эта вторая может стать к первой ближе, чем на любую данную величину, как бы мала ни была последняя…». Ы 1786 г. Берлинская академия наук объявила конкурс на строгое обоснование анализа бесконечно малых. Премию на конкурсе получил французский ученый С. Люилье, который развил идеи Даламбера, впервые ввел знак предела в виде lim, а под производной (по терминологии Люилье, «дифференциальным отношением») понимал В прочем работа Люилье не получила широкой известности, тем более что автор не развил теорию пределов и дифференциальное исчисление сколько-нибудь подробно.

Центральной фигурой в математике XVIII в. был Л. Эйлер. Другие крупные ученые XVIII в.: Ж.Л. Лагранж, И. Бернулли, П.С. Лаплас и др.

Леонард Эйлер (1707−1783) родился в Базеле (Швейцария), был сыном пастора. Окончил Базельский университет. Хотя он был выдающимся студентом, места преподавателя в своем университете ему не нашлось. Его друзья, сыновья И. Бернулли – Даниил и Николай в 1725 г. уехали в Петербург для работы в только что открывшейся академии наук. По их рекомендации в 1727 г. в Петербург был приглашен и Эйлер. Дальнейшую его жизнь можно разделить на три периода.

1.В первый период жизни в Петербурге (1727−1741) Эйлер опубликовал более 50 работ и подготовил к печати еще более 80 работ по математике, механике, астрономии. В 1738 г. во время напряженной работы над астрономическими вычислениями он ослеп на один глаз.

2.В Петербурге в царствование Анны Ионновны жить стало беспокойно, а условия для работы в академии стали неблагоприятными. В 1741 г. Эйлер принял предложение прусского короля Фридриха II переехать в Берлин в только что основанную академию наук и проработал там до 1766 г. В Берлинской академии он был директором математического отделения и занимал должность вице-президента. За это время Эйлер написал около 300 работ, часть которых – книги, иногда в 2−3 томах. Примерно половину работ он посылал для опубликования в Петербург. В Петербурге Эйлер числился почетным академиком и получал оттуда жалование. К нему для стажировки присылали из Петербургской академии молодых ученых, он писал отзывы на работы по математике и закупал для академии книги и инструменты.

3.Третий период жизни Эйлера составляет его работа в Петербурге (1766−1783). В 1766 г. он по приглашению Екатерины II вернулся в Петербург. Вскоре после возвращения Эйлер ослеп на другой глаз, но его научная деятельность не ослабела, а усилилась − он диктовал статьи и книги своим ученикам. За этот последний период жизни он создал работ больше, чем за время жизни в Берлине; после его смерти работы Эйлера печатались в изданиях академии еще 80 лет

Эйлер – наиболее плодовитый в истории науки ученый. Им написано 850 сочинений, из которых 40 – большие, нередко многотомные монографии. В 1909 г. в Швейцарии было начато издание полного собрания его сочинений. Планировалось издать 72 тома, но материала оказалось гораздо больше. Эйлер одержал на конкурсах различных академий по механике, физике, технике больше побед, чем кто-либо из ученых XVIII в.

Отметим главные особенности творчества Эйлера.

Он стремился систематизировать всю математику того времени, а также смежные дисциплины. Это удалось ему в математическом анализе, аналитической геометрии и теории чисел.

Он основал несколько больших дисциплин, которые до него существовали лишь в зачаточном виде: теорию дифференциальных уравнений – обыкновенных и в частных производных, вариационное исчисление, теорию чисел. Многие глубокие идеи Эйлера были развиты лишь через несколько десятков лет: внутренняя геометрия поверхностей, применение анализа в теории чисел, эйлерова

характеристика многогранников, которая сейчас относится к топологии, и др.

В его научном творчестве очень велик удельный вес практики: около 40% работ Эйлера посвящено прикладной математике, механике, физике, астрономии, оптике и т.д. Назовем несколько его монографий: «Механика ( 2 тома), « Теория движения Луны», «Диоптрика» (3 тома), «Теория движения твердых тел», трехтомные «Письма к немецкой принцессе» (популярное изложение физики и астрономии вместе с примыкающими к ним вопросами философии) и др.

Еще одна особенность наследия Эйлера – алгоритмичность: он стремится, особенно в работах по математике, довести решение проблемы до алгоритма, удобного для преобразований и вычислений.

Главное место в работах Эйлера по математике занимает математический анализ. Из 30 томов математической серии его собрания сочинений 19 посвящены математическому анализу. Кроме того, он широко применяет анализ к механике, геометрии и др.

Крупнейшими монографиями Эйлера по математике являются следующие: двухтомное « Введение в анализ бесконечных» (1748); «Дифференциальное исчисление» (1755); трехтомное « Интегральное исчисление» (1768−1770); «Метод нахождения кривых линий, обладающих свойствами максимума либо минимума» − работа, посвященная вариационному исчислению; двухтомная « Универсальная арифметика» (1768,1769) – учебное пособие по алгебре и диофантовому анализу.

Здесь мы рассмотрим трилогию, посвященную математическому анализу.

1. «Введение в анализ бесконечных»

В первом томе этого сочинения рассматривается учение о функции – та его часть, в которой не используется бесконечно малые. Второй том посвящен, как мы знаем (§ 25, п. 4), аналитической геометрии, а также некоторым вопросам алгебраической геометрии. Он идейно связан с первым томом.

Сначала Эйлер дает определение функции как аналитического выражения. Затем он приводит следующую классификацию функций в зависимости от вида задающих их аналитических выражений рис.44

Функции

Алгебраические Трансцендентные

Рациональные Иррациональные Тригономе- Показательная и

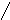
трические логарифмическая

Целые Дробные

Рис. 44

Похожая классификация функций приводится и в современных учебниках математического анализа, со следующим отличием – в настоящее время к трансцендентным функциям относят гораздо более широкий класс функций, чем у Эйлера: обратные тригонометрические, степенную функцию с иррациональным показателем, целую часть числа и многие другие.

Эйлер впервые стал рассматривать функции явные и неявные, взаимно обратные, алгебраические и трансцендентные, честные и нечестные, однозначные и многозначные. Он одним из первых дал определение логарифма как показателя степени и стал изучать показательную и логарифмическую функцию. Он изложил тригонометрию в почти современном виде (см. § 23).

Эйлер допускал как действительные, так и мнимые значения аргумента. Он впервые стал рассматривать элементарные функции в комплексной области, в частности, вывел формулы, которые теперь носят его имя:

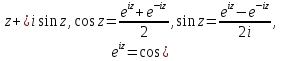
где 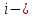мнимая единица,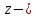комплексное число. При этом Эйлер широко пользуется разложениями элементарных функций в степенные ряды, допуская как действительные, так и мнимые члены ряда.

2. «Дифференциальное исчисление»

Сначала автор рассматривает дифференциалы функций одной и нескольких переменных, а затем – их предложения к теории рядов, экстремумам и предельным значениям неопределенных выражений.

Изложение, в общем, близко к изложению Лейбница; например; Эйлер постоянно применяет принцип пренебрежения бесконечно малыми высших порядков. Но имеются и существенные отличия. Скажем, он рассматривает анализ бесконечно малых как своего рода исчисления нулей. Главное же – для Эйлера здесь основным понятием является не дифференциал, как у Лейбница, а «отношение исчезающих приращений, получаемых каким-либо функциями, когда переменному количеству, функциями которого они являются, дается исчезающее приращение», т. е. говоря, современным языком, предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю,− производная.

Геометрических приложений дифференциального исчисления у Эйлера нет.

3. «Интегральное исчисление»

Здесь излагаются интегрирование функций одной переменной, дифференциальные уравнения – обыкновенные и в частных производных, а также элементы вариационного исчисления.

Интегральное исчисление у Эйлера есть « метод, посредством которого по данному соотношению между дифференциалами количеств находят соотношение между самими количествами». Интегралом данной функции он называет функцию, которая имеет своим дифференциалом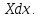Отсюда видно, что под интегралом Эйлер понимает неопределенный интеграл; при этом он регулярно пользуется постоянной интегрирования.

Эйлер существенно продвинул вперед технику интегрирования. Например, при вычислении интеграла 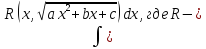рациональная функция от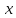и от квадратного корня, он ввел так называемые подстановки Эйлера, с помощью которых этот интеграл приводится к интегралу от рациональной функции. Он разработал также способы интегрирования тригонометрических функций.

Имеется ли у него понятие об определенном интеграле как пределе интегральных сумм? В явной форме – нет, так как, по Эйлеру, дифференциал равен нулю, а следовательно, сумма дифференциалов равна нулю. При вычислении определенного интеграла он обычно пользуется формулой Ньютона-Лейбница. Четко идея определенного интеграла как предела была выражена французским ученым С.Ф. Лакруа в самом конце XVIII в., а окончательно оформлена О.Коши в XIX в.

Остановимся еще на решении обыкновенных дифференциальных уравнений в «Интегральном исчислении». Многое здесь, прежде всего, относящееся к уравнениям первого порядка, было получено до Эйлера Лейбницем, братьями Бернулли и др. и вошло в данное сочинение. Эйлер уделил особое внимание уравнению в полных дифференциалах и уравнению вида

которое не является уравнением в полных дифференциалах, но приводится к нему с помощью умножения на некоторых множитель – так называемый интегрирующий множитель. Вопросы математического анализа у Эйлера рассмотрены не только в трилогии, но и в многочисленных статьях.

Из остальных математиков XVIII в. остановимся на Лагранже.

Жозер Луи Лагранж (1736 – 1813) в математике был самоучкой. Сначала преподавал математику в артиллерийской школе в Турине, затем долгое время работал в Берлинской академии наук и даже был ее президентом, а к концу жизни – в Политической школе в Париже. Занимался математическим анализом, вариационным исчислением, теорий чисел, алгеброй и механикой. Крупнейшие его работы – «Теория аналитических функций» и «Аналитическая механика».

В первой из них он, в частности, определяет производную чисто алгебраически, без пределов и бесконечно малых, с помощью бесконечных рядов: если для функции 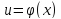выполняется равенство

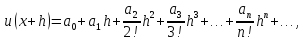
то коэффициенты 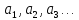называются производными функции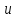в точке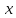соответственно первого, второго, третьего и т.д. порядков. Эти производные Лагранж обозначает следующим образом:

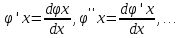
(без скобок). Он одним из первых ввел термин « производная».

Однако остаются открытыми вопросы: когда функция разлагается в степенной ряд – Тейлора? Как получить это разложение? (Ряд Тейлора к этому времени был хорошо известен.) Первый вопрос, по мнению Лагранжа, не требовал ответа: он считал само собой разумеющимся, что любую функцию. заданную формулой, можно разложить в степенной ряд. Что касается второго вопроса, то на него в XVIII в. отвечали по-разному, в зависимости от вида функции: например, для разложения функции 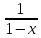и некоторых других дробно-рациональных функций применяли деление числителя дроби на знаменатель «углом», часто использовали дифференцирование и интегрирование степенных рядов, и т.д.

Лагранж, исходя из ряда Тейлора, вывел формулу Тейлора, а из последней формулы – так называемую теорему Лагранжа о средних значениях, связанную с формулой