§ 22. Решение уравнений третьей и четвертой степени

Проблема решения уравнений третьей и четвертой степени в радикалах не вызывалась особой практической необходимостью. Ее появление косвенным образом свидетельствовало о постепенном переходе математики к более высокому уровню ее развития, когда математическая наука развивается не только под влиянием запросов практики, но и в силу своей внутренней логики. После решения квадратных уравнений естественно было перейти к решению кубических уравнений.

Уравнения третьей и четвертой степени были решены в Италии в XVI в.

Итальянские математики рассматривали три вида кубических уравнений:

1. 

Рассмотрение трех видов кубических уравнений вместо одного 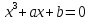связано с тем, что, хотя математикиXVI в. были знакомы с отрицательными числами, но они еще долго не считались настоящими числами, и ученые стремились записывать уравнения только с положительными коэффициентами.

Исторически сложилось так, что сначала алгебраисты занялись уравнением первого типа

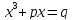. (1)

Первоначально его решил профессор Болонского университета Сципион дель Ферро, но полученное решение не опубликовал, а сообщил его своему ученику Фиоре. С помощью секрета решения этого уравнения Фиоре победил на нескольких математических турнирах. Тогда такие турниры были распространены в Италии. Заключались они в том, что два противника в присутствии нотариуса обменивались заранее обусловленным числом задач и договаривались о сроке для их решения. Победитель получал известность и нередко выгодную должность. В 1535 г. Фиоре вызвал на такой поединок любого, кто хочет с ним сразиться. Вызов принял Тарталья.

Никколо Тарталья (1500-1557) рано остался сиротой и вырос в бедности, не получив никакого образования. Тем не менее он был хорошо знаком с математикой того времени и зарабатывал себе на жизнь частными уроками математики. Незадолго до поединка с Фиоре он сумел самостоятельно решить уравнение (1). Поэтому когда противники встретились, Тарталья смог за несколько часов решить задачи Фиоре; все они оказались на уравнении (1). Что касается Фиоре, то он и за много дней не решил ни одной из 30 разнообразных задач Тартальи. Победителем турнира был признан Тарталья. Известие о его победе распространилось по всей Италии. Он стал заведовать кафедрой математики в университете города Вероны.

Метод Тартальи заключался в следующем. Он полагал в уравнении (1) 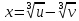, гдеu и v – новые неизвестные. Получим:

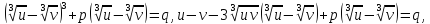
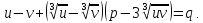
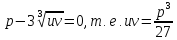Положим в последнем уравнении . Образуется система уравнений

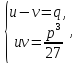
которая сводится к квадратному уравнению. Из нее находим:

,

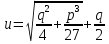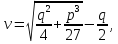
откуда

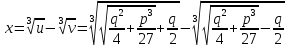(2)

Вскоре после турнира Тарталья легко решил кубические уравнения второго и третьего типа. Например, для уравнения второго типа 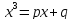он применил подстановкукоторая привела к формуле

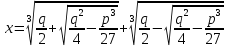(3)

Известие об успехи Тартальи дошло до Кардано. Джироламо Кардано (1501-1576) окончил медицинский факультет университета в Павии и был врачом в Милане. Он являлся ученым, не менее талантливым, чем Тарталья, и гораздо более разносторонним: он занимался медициной, математикой, философией и астрологией. Кардано задумал написать книгу энциклопедического характера по алгебре, и она была бы неполна без решения кубических уравнений. Он обратился к Тарталье с просьбой сообщить его способ решения этих уравнений. Тарталья не соглашался, и тогда Кардано поклялся на Евангелии никому не сообщать секрета решения кубических уравнений. По-видимому, Тарталья собирался сам написать книгу по алгебре, включив в нее и свое открытие, но из-за занятости и из-за того, что издание было делом дорогостоящим, откладывал свое намерение. В конце концов в 1545 г. Кардано выпустил свою монографию под названием «Великое искусство», в которую вошло и открытие «моего друга Тартальи». Тарталья был разгневан нарушением клятвы и выступил в печати с разоблачением Кардано. Кончилось тем, что лучший ученик Кардано вызвал Тарталью на публичный поединок. Поединок состоялся в 1548 г. в Милане и закончился, при не вполне ясных обстоятельствах, поражением Тартальи. Формулы корней кубического уравнения получили в истории название формул Кардано, хотя сам Кардано в своей книге и не приводил формул, а излагал алгоритм решения кубического уравнения.

Книга Кардано «Великое искусство» сыграло значительную роль в истории алгебры. В частности, в ней он доказал, что полное уравнение третье степени с помощью подстановки сводится к уравнению без члена с квадратом неизвестного, т.е. к одному из трех видов кубических уравнений, рассмотренных в начале параграфа. Осовременивая изложение, возьмем кубическое уравнение общего вида

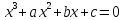
с произвольными по знаку коэффициентами вместо тех нескольких типов кубических уравнений, которыми занимался Кардано, и положим в нем

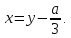
Тогда

.

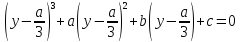Нетрудно проверить, что последнее уравнение не содержит члена с квадратом неизвестного, так как сумма членов, содержащих 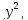равна нулю:

.

Аналогично Кардано доказал, что в полном уравнении четвертой степени можно избавиться от члена с кубом неизвестного. Для этого в уравнении четвертой степени общего вида

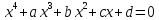
достаточно положить .

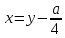Позднее Ф. Виет знакомое нам кубическое уравнение 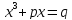решил с помощью остроумной подставки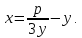Будем иметь:

.

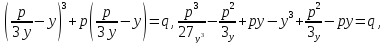
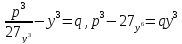Положим в последнем уравнении 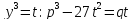. Из полученного квадратного уравнения находимt; затем вычислим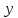и, наконец,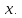

Уравнение четвертой степени решил Феррари. Он решал его на примере

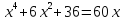(4)

(без члена с кубом неизвестного), но вполне общим способом.

Прибавим к обеим частям уравнения (4) 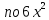, с тем, чтобы дополнить левую часть до квадрата суммы:

Теперь прибавим к обеим частям последнего уравнения сумму

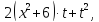где t – новое неизвестное:

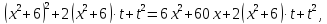
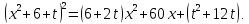(5)

Так как левая часть уравнения (5) есть квадрат суммы, то и правая часть есть квадрат, а тогда дискриминант квадратного трехчлена равен нулю: 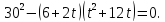Впрочем, вXVI в. это уравнение писали в виде

(6)

Уравнение (6) является кубическим. Найдем из него t уже знакомым способом, подставим это значение t в уравнение (5) и извлечем из обеих частей полученного уравнения квадратный корень. Образуется квадратное уравнение(точнее, два квадратных уравнения).

Приведенный здесь способ решения уравнения четвертой степени вошел в книгу Кардано.

По воззрениям того времени, правило решения кубического уравнения второго типа по формуле (3) нельзя применять в том случае, когда

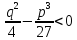; c современной точки зрения, в этом случае приходится проводить операции над мнимыми числами. Например, уравнение

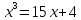имеет действительный корень 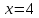; кроме того, оно имеет еще два действительных (иррациональных) корня. Но по формуле (3) получаем:

Каким образом из мнимых («воображаемых», как тогда говорили) чисел получается действительное число? Это случай кубического уравнения получил название неприводимого.

Подробно неприводимый случай разобрал итальянский математик Рафаэль Бомбелли в книге «Алгебра», изданной в 1572 г. В формуле (3) он объяснил эту ситуацию тем, что первый кубический корень равен 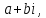а второй –a-bi (где a и b- действительные числа, t-мнимая единица), так что их сумма дает

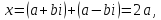
т.е. действительное число.

Бомбелли привел правила действий над комплексными числами.

После выхода книги Бомбелли математикам постепенно становится ясно, что в алгебре без комплексных чисел не обойтись.