§ 40. Создание неевклидовой и многомерной геометрии. Аксиоматизация геометрии

1.Со времени Евклида до XIX в., более 2000 лет, делались многократные попытки доказать пятый постулат Евклида. При этом обычно пятый постулат рассматривался в следующей форме: через точку, лежащую вне прямой, в той же плоскости можно провести только одну прямую, не пересекающую данную. Наиболее известны попытки доказательства постулата Ламберта, Саккери (XVIIIв.), Швейкарта, Тауринуса (XIX в.) Постепенно формируется убеждение, что пятый постулат невозможно доказать с помощью других постулатов и аксиом Евклида. На этом пути стали складываться идеи неевклидовой геометрии.

Создателями неевклидовой геометрии были К. Гаусс, Н.И. Лобачевский и Я. Бояи.

Первым здесь был Гаусс. Но он ничего не опубликовал по неевклидовой геометрии, опасаясь быть непонятым. После смерти Гаусса в его бумагах нашли заметки по неевклидовой геометрии.

Венгерский ученый Янош Бояи свое сочинение по неевклидовой геометрии «Аппендикс» опубликовал в 1832 г. в качестве приложения к популярной книге отца, математика. Отец послал работу на отзыв своему другу Гауссу. Гаусс работу одобрил, но добавил, что идеи неевклидовой геометрии ему уже давно известны. Отзыв Гаусса нанес Я. Бояи сильный психологический удар, и он больше не занимался неевклидовой геометрией, а вскоре – и вообще математикой.

Слава первой публикации по неевклидовой геометрии принадлежит нашему соотечественнику Лобачевскому.

Николай Иванович Лобачевский (1792−1956) родился в Нижнем Новгороде в семье бедного чиновника. Окончил Казанский университет. С 1816 г. он – профессор этого университета, с 1820 – декан физико-математического факультета, а в 1827-1845 гг. – ректор университета. Как ректор, он показал себя блестящим организатором; под его руководством было построено большинство университетских зданий. В математике занимался геометрией, математическим анализом и алгеброй.

11(23) февраля 1826г.Лобачевский на собрании физико-математического отделения университета сделал первый доклад по неевклидовой геометрии. В 1829−1830 гг. он опубликовал первую работу по новой геометрии « О началах геометрии» в журнале университета «Казанский вестник». Всю жизнь он занимался распространением идей неевклидовой геометрии, напечатав ряд работ: « Воображаемая геометрия», «Новые начала геометрии с полной теории параллельных», «Пангеометрия», «Геометрические исследования» (последняя – на немецком языке). При жизни Лобачевского его работы или не замечали, или не понимали; единственным, кто дал им высокую оценку, был Гаусс, но только в частной переписке.

Геометрия Лобачевского в той своей части, которая не зависит от аксиомы о параллельных (так называемая абсолютная геометрия), по существу не отличается от геометрии Евклида. В остальном же отличия весьма существенны. Главное – иная формулировка аксиомы о параллельных: через точку вне прямой в той же плоскости можно провести не менее двух прямых, не пересекающих данную прямую. Если принять эту формулировку, то отсюда следует, что таких прямых – бесконечное множество. Они образуют пучок прямых.

Укажем некоторые другие следствия новой аксиомы о параллельных. Сумма углов треугольника меньше 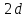. При увеличении сторон треугольника эта сумма уменьшается. Появляется еще один признак равенства треугольников по трем углам; следовательно, треугольник определяется своими углами. не существует подобных и не равных треугольников и многоугольников.

Геометрия Лобачевского стала получать признание только тогда, когда появились ее интерпретации. Первую такую интерпретацию построил итальянский математик Э. Бельтрами в 1868 г., используя свои исследования по дифференциальной геометрии, но она относилась лишь к части плоскости Лобачевского. Полную интерпретацию впервые дал немецкий ученый Ф. Клейн в 1871г. Для этого он использует внутренность круга единичного радиуса.

«Точками» назовем точки внутри круга, «прямыми» − хорды круга без конечных точек, «параллельными прямыми» − хорды с общим концом. Все предложения абсолютной геометрии здесь выполняются. Выполняется и аксиома параллельности Лобачевского. «Расстояние» между двумя точками 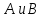Клейн определяет с помощью двойного отношения четырех точек. По существу, здесь используется аналитическая геометрия проективного пространства, построенная Плюккером (см. § 39, п. 2).

Своей интерпретацией, которая охватывает всю геометрию Лобачевского на плоскости, Клейн доказал, что геометрия Лобачевского непротиворечива в той же мере, как и геометрия Евклида, а следовательно, имеет такое же право на существование в науке.

После Клейна были найдены и другие интерпретации геометрии Лобачевского: например, французский ученый А. Пуанкаре в 1882 г. построил интерпретацию, использующую теорию функций комплексной переменной.

Однако используется ли геометрия Лобачевского на практике? В XXв. были найдены серьезные ее применения в теории относительности А. Эйнштейна и в квантовой механике.

Одним из важнейших последствий открытия геометрии Лобачевского стало создание новых неевклидовых геометрий, в первую очередь геометрия Римана.

В геометрии Б. Римана, построенной в 1854 г., вместо аксиомы о параллельных вводится такая аксиома: любая пара прямых, лежащих в одной плоскости, пересекается. Отсюда можно вывести, что любая прямая замкнута, наподобие окружности в геометрии Евклида. Тогда для трех точек 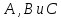понятие «лежать между» теряет определенный смысл: каждая из точек лежит между двумя другими. Далее, на плоскости Римана прямая не делит эту плоскость на две полуплоскости; сумма углов треугольника большелюбая прямая конечна.

Для того, чтобы убедиться в непротиворечивости геометрии Риана, достаточно построить ее интерпретацию, пользуясь геометрией Евклида.

Рассмотрим сферу единичного радиуса (рис. 47). «Точкой» назовем любую пару диаметрально противоположных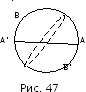

точек сфер. «Прямой» будет называть любую большую окружность сферы. «Плоскостью»назовем саму сферу.

Фраза «точка лежит на прямой» означает, что две диаметрально противоположные точки сферы лежат на одной большой окружности сферы.

Теперь проведем справедливость некоторых аксиом абсолютной геометрии, аксиомы Римана и некоторых предложений геометрии Римана.

Через любые две «точки» проходит одна только одна «прямая», так как через любые две пары диаметрально противоположных точек сферы проходит одна и только одна большая окружность сферы. Любые две различные «прямые» пересекаются, причем в единственной «точке», так как любые две различные большие окружности пересекаются, причем в единственной паре диаметрально противоположных точек сферы. Каждая «прямая» замкнута и конечна.

«Треугольник» изображается двумя сферическими треугольниками 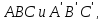сторонами которого являются дуги больших окружностей. «Углом» треугольника назовем соответствующий двугранный угол трехгранного угла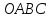с вершиной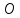. Известно, что сумма углов сферического треугольника больше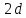(например, если взять равносторонний треугольник, у которого каждая из сторон равна четверти большой окружности, то у него все углы – прямые, а следовательно, их сумма равна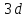), т.е. сумма «углов треугольника» в геометрии Римана больше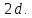

2.Рассмотрим историю создания многомерной геометрии.

В 1844 г. немецкий ученый Г.Грассман опубликовал первое крупное сочинение по многомерной геометрии «Учение о линейном многообразии». Учением о линейном многообразии он называл геометрию многомерных пространств. Грассман ввел мерное линейное пространство, где вообще говоря,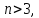и рассмотрел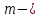мерные плоскости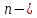мерного пространства.

В 1875 г. французский ученый К. Жордан издал работу «Очерк геометрии измерений. В ней он, существенно использовав результаты нескольких своих предшественников, ввел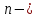мерноеевклидово пространство, впервые придав теории этого пространства вид, близкий к современному. Жордан определил точку 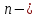мерного пространства как последовательность (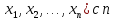действительными членами, а расстояние между точками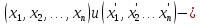как

.

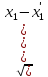Последняя формула является обобщением формул расстояния между двумя точками двумерного и трехмерного евклидового пространства. Линейное уравнение с координатами точки определяет у Жордана плоскость. Далее он проверяет обычные свойства плоскости и расстояния. Оказалось, что все они выполняются, за исключением такого: две плоскости, имеющие общую точку, имеют по меньшей мере еще одну общую точку. Если это свойство выполнено, то пространство может быть только трехмерным, если же нет, т.е. существуют две плоскости с единственной общей точкой, то пространство, как минимум, четырехмерно.

Совершенно с другой стороны к многомерной геометрии подошел немецкий математик Бернгард Риман (1826−1866). За свою короткую жизнь он опубликовал немного работ, но каждая из них была событием в математике. Круг его интересов в математике был весьма широк: он занимался геометрией, математическим анализом, теорией функций комплексной переменной, математической физикой и др. Пожалуй, он больше, чем любой другой ученый XIX в., повлиял на развитие современной математики.

В 1854 г. Риман в Геттингенском университете прочитал пробную лекцию «О гипотезах, лежащих в основании геометрии». В ней он поставил вопрос о природе самого пространства, а главной задачей геометрии объявил исследование пространств. Риман рассмотрел аналитически пространство 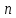измерений, вообще говоря, не являющееся, евклидовым, в котором задается закон измерения расстояний между двумя точками, причем так, чтобы вблизи каждой точки он совпадал с евклидовым с точностью до бесконечно малой высшего порядка. Исходя из формулы расстояния, он выводил свойства самого пространства.

Среди различных линий, соединяющих две данные точки, особое место занимают кратчайшие (геодезические) линии. С помощью геодезических линий Риман определяет важнейшее понятие многомерной геометрии − кривизну пространства.

Для определения кривизны пространства в данной точке 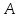нужно из этой точки провести две геодезические линии, касающиеся данного двумерного направления, соединить какие-либо две точки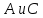этих линий третьей геодезической линией и вычислить сумму углов и площадь образовавшегося «геодезического» треугольника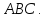Кривизной пространства в точке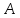в данном двумерном направлении называется предел отношения углового избытка треугольника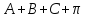к его площади при стягивании треугольника в точку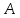. Угловой избыток может быть как положительным, так и отрицательным, поэтому кривизна может быть как положительной, так и отрицательной. Для трехмерного евклидова пространства угловой избыток равен нулю, поэтому кривизна евклидова пространства постоянна и равна нулю.

Искривленные многомерные пространства, введенные Риманом, в настоящее время получили название римановых пространств, а их геометрия – римановой геометрии. Примерами римановых пространств, кроме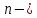мерного евклидова пространства, могут служить и пространства, в которых имеют место неевклидовы трехмерные геометрии Лобачевского и Римана.

3.Перейдем к истории классификации геометрических теорий.

Во второй половине XIX в. весьма актуальными стали вопросы: что объединяет между собой различные геометрические теории? Как их классифицировать?

Первым на эти вопросы ответил Б. Риман в той же своей знаменитой лекции в университете Геттингена в 1854 г. В основу он положил метрический принцип. Для построения геометрической теории нужно знать:1)множество элементов; 2) координаты этих элементов; 3) закон измерения расстояний между близкими друг к другу элементами.(Об этом частично уже упоминалось в п.2).

Однако осуществить полностью такую широкую программу классификации геометрических теорий в то время было невозможно. Дело в том. что точки пространств могли быть весьма разнообразной природы, и каждый раз возникал вопрос: что понимать под расстоянием между двумя точками? Средств дифференциальной геометрии для ответа на этот вопрос было явно недостаточно. Риман не смог создать нового аналитического аппарата, соответствующего его программе. Лишь в начале XX в., когда было открыто тензорное исчисление, оказалось, что оно дает наиболее подходящий, хотя и сложный, аппарат для указанной цели.

Другу. программу классификации геометрических теорий предложил немецкий математик Ф. Клейн. Он изложил ее в лекции, прочитанной в 1872 г. в университете г. Эрлангена в связи со вступлением на должность профессора, поэтому она позднее получила название Эрлангенской программы Клейна.

В этой лекции Клейн существенно использовал проективную геометрию, которой он тогда занимался, и теорию групп, которая во второй половине XIX в. интенсивно развивалась. Так как в классификации Клейна главную роль играет проективная геометрия, то ее называют еще проективной, или, реже, теоретико-групповой.

По Клейну. для построения геометрии нужно задать некоторое множество элементов и группу преобразований, т.е. отображений, этого множества на себя. Геометрия должна изучать инварианты таких преобразований.

Например, геометрия Евклида изучает инварианты движений и преобразования подобия. причем группа движений является подгруппой группы подобий («главной группы» евклидова пространства); аффинная геометрия изучает инварианты аффинных преобразований, где группа подобий есть подгруппа группы аффинных преобразований; проективная геометрия рассматривает инварианты проективного преобразования коллинеации (когда точка прямой переходят в точки прямой),причем группа аффинных преобразований есть подгруппа группы коллинеаций проективного пространства. Неевклидовы геометрии Лобачевского и Римана можно рассматривать как части проективной геометрии, где изучаются инварианты некоторой подгруппы группы коллинеаций проективного пространства.(В последнем случае Клейн использовал одну из работ А. Кэли.)

Приведенная здесь классификация относится только к трехмерному пространству. Но далее Клейн подобным же образом классифицирует геометрии в многомерных пространствах.

Классификация у Клейна проще, чем у Римана, но и гораздо менее объемлюща; например, из нее выпадает дифференциальная геометрия. Идея Клейна о том, что геометрию можно построить на любом множестве, в котором установлена группа преобразований, сохраняет свое значение до наших дней не только для классификации геометрических теорий, но и для построения новых областей геометрии.

4.Наряду с созданием неевклидовой и многомерной геометрии весьма актуальной стала проблема создания аксиоматики обычной трехмерной евклидовой геометрии.

Мы знаем, что система постулатов и аксиом в «Началах» Евклида неполна в следующем смысле: ее недостаточно для того, чтобы любое предложение, имеющее смысл в рамках евклидовой геометрии. можно было строго логически доказать или опровергнуть. Сам Евклид при доказательстве некоторых предложений своей геометрии был вынужден делать отдельные допущения, которые отсутствовали в его системе постулатов и аксиом или могли быть выведены из этой системы. Вопрос интерпретации геометрии Лобачевского с помощью геометрии Евклида также требовал создания полной и непротиворечивой аксиоматики евклидовой геометрии. Кроме того, история пятого постулата, которая к XIX в. насчитывала уже более двух тысяч лет, выдвинула задачу доказательства независимости аксиом геометрии друг от друга − не только пятого постулата, но и других постулатов и аксиом Евклида, а также тех аксиом, которые должны были быть добавлены к ним в целях полноты.

Первые шаги в решении указанной проблемы были сделаны в семидесятые годы XIX в., когда Г. Кантор и Р. Дедекинд ввели аксиому непрерывности и выделили предложения, при доказательстве которых она применяется. Затем М. Паш разработал аксиомы порядка и конгруэнтности, а Д. Пеано установил основы, на которых можно осуществить логическое построение геометрии Евклида. Наконец, в 1899 г., в самом конце XIX в., появилась книга « Основания геометрии» немецкого математика Д. Гильберта, в которой впервые была изложена полная система аксиом евклидовой геометрии и на этой базе построена геометрия.

Основными, неопределяемыми понятиями у Гильберта являются точка, прямая и плоскость. Его система аксиом состоит из следующих групп: аксиомы принадлежности (основное, неопределяемое отношение – «принадлежность» или «инцидентность»), аксиомы порядка (основное отношение «лежать между», применяемое в случае, когда три точки принадлежат одной прямой), аксиомы конгруэнтности (основное отношение – «конгруэнтный» или равный), аксиома параллельности и аксиомы непрерывности.

Аксиома параллельности в книге Гильберта формулируется следующим образом: если 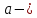производная прямая и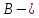точка, лежащая вне прямой, то через точку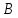в плоскости, определяемой ими, можно провести не более одной прямой, не пересекающей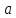. То, что одну такую прямую провести можно, легко доказать на основании предыдущих аксиом; поэтому из аксиомы параллельности (и предыдущих аксиом) следует, что через точку вне данной прямой можно провести только одну прямую, не пересекающую данную.

Группа аксиом непрерывности состоит из двух аксиом. Аксиома Архимеда: каковы бы ни были отрезки 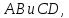существует такое натуральное число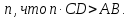Кантора: пусть на произвольной прямой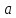дана бесконечная последовательность отрезков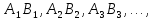из которых каждый последующий лежит внутри предыдущего; пусть при этом не существует отрезка, лежащего внутри всех отрезков данной последовательности, Тогда на прямой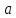существует одна и только одна точкалежащая внутри всех отрезков.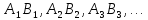

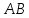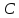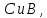Можно доказать, что две аксиомы непрерывности эквивалентны одной – аксиоме Дедекинда: для любого сечения во множестве точек отрезка существует одна и только одна точка, что любая точка междупринадлежит одному классу сечения, а любая точка, лежащая междупринадлежит другому классу. (Определение сечения см. в §35.)

На основании рассмотренной аксиоматики можно доказать все обычные теоремы геометрии Евклида. Затем Гильберт установил непротиворечивость этой системы аксиом с помощью построения числовой модели, точнее, свел ее к непротиворечивости арифметики действительных чисел, установил независимость групп аксиом и полноту системы.

Как такая аксиоматика соотносится с действительностью? Наглядные пространственные представления играют очень большую роль при самом построении аксиоматики. Но в готовой уже системе аксиом не должно быть ссылок на ту или иную конкретную ее интерпретацию. Пространственные представления похожи на леса, которые необходимы при строительстве аксиоматического здания, но должны быть убраны, когда строительство закончено. Теперь можно рассматривать различные интерпретации геометрии, построенной на базе аксиоматики Гильберта, вводя основные понятия и отношения между ними так, чтобы выполнялись все аксиомы.

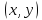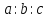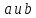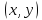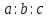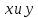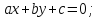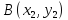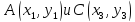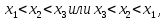Рассмотрим пример такой интерпретации. Назовем «точкой» любую прямую упорядоченную пару действительных чисел, «прямой» − упорядоченное отношениелюбых трех действительных чисел, при условии, что по меньшей мере одно из чиселне равно нулю. Фраза «точкапринадлежит прямой» будет означать, что числаудовлетворяют уравнениюпод фразой «точкалежит между точками» будем понимать, чтопри условии, что точкилежат на одной прямой. И т.д. Можно проверить, что все аксиомы Гильберта здесь выполняются. Именно с помощью этой арифметической модели Гильберт свел непротиворечивость своей аксиоматики к непротиворечивости арифметики действительных чисел.

Гильбертова аксиоматика геометрии Евклида была не единственной. В 1918 г. немецкий математик Г. Вейль издал работу со своей аксиоматикой, в которой основным, неопределяемым понятием является понятие вектора. Существуют и другие аксиоматики; в некоторых из них аксиомы конгруэнтности заменяются аксиомами движения.

В заключении остановимся на вопросе о распространении в математике аксиоматического метода. В конце XIX в. было создано несколько систем аксиом арифметики натуральных чисел; самой неизвестной из них является аксиоматика Пеано. В начале XX в. строятся аксиоматические теории множеств (Э. Цермело, А. Френкелем, Д. Нейманом и др.). В XX в. были построены аксиоматики математической логики, проективной геометрии, неевклидовых геометрий Лобачевского и Римана, дифференциальной геометрии, теории вероятностей и других дисциплин. Аксиоматический метод проник в алгебру. Мало того, некоторые нематематические науки также стали преобразовываться на аксиоматической основе. Наиболее известный пример – механика; начало такой перестройке механике положил еще Ньютон в работе «Математические начала натуральной философии».