§ 41 Проблемы Гильберта

Математику XX века нам неизбежно придется рассматривать лишь в обзорном порядке. Более или менее ясно, что она представляла собой в первой половине века; сложнее обстоит дело со второй половиной: ведь для того, чтобы объективно оценить математику того или иного периода, требуется известная дистанция во времени. Проблема и в том, что в XX в. развивались, главным образом, такие области математики, которые находят отражение в вузовских математических курсах.

XX век был великой эпохой в истории математики. Достижения математики в этом столетии, пожалуй, превосходят все, что было сделано в ней за предшествующие две с половиной тысячи лет, − с того времени, когда математика стала превращаться в дедуктивную науку.

Сопоставим математику начала и конца века. На Втором международном математическом конгрессе, который состоялся в Париже в 1900 г., имелись четыре основные секции: арифметики и алгебры, анализа, геометрии, механики и математической физики. На современных международных математических конгрессах, число основных секций много больше: математическая логика и основания математики; теория чисел; геометрия; алгебраическая геометрия; алгебра; группы Ли и теория представлений; комплексный анализ; теория функций действительной переменной и функциональный анализ; теория вероятностей и математическая статистика; обыкновенные дифференциальные уравнения; дифференциальные уравнения с частными производными; математическая физика; численные методы и теория вычисления; дискретная математика и комбинаторика; математические аспекты информатики; приложения математики к нефизическим наукам. Многие из перечисленных областей появились или оформились лишь в XX в.

На упоминавшемся выше Втором международном математическом конгрессе, на рубеже двух веков, немецкий ученый Д. Гильберт сформулировал 23 крупные проблемы математики, которые должны быть решены в XX в.; они получили название проблем Гильберта.

Давид Гильберт (1862-1943) был профессором математики в Геттингенском университете, возглавлял крупную научную школу. Он был математиком –универсалом, из числа тех ученых, которых за три последних столетия было немного: в XVIII в. – Л. Эйлер, в XIX− К. Гаусс и О. Коши, в XX в. – Д. Гильберт. Гильберт занимался многими областями математики: алгеброй, теорией чисел, геометрией, математической физикой, функциональным анализом, математической логикой и др.

Рассмотрим некоторые из проблем Гильберта.

1.Проблема континуума: существует ли множество, промежуточное по мощности между счетным множеством (например, множеством натуральных чисел) и множеством действительным чисел?

Решение проблемы оказалось неожиданным: при существующей аксиоматике теории множеств гипотезу о существовании такого множества нельзя ни опровергнуть (К. Гедель, 1936), ни доказать (П. Коэн,1963). Отсюда следует, что аксиоматика теории множеств неполна.

2.Найти алгоритм решения алгебраических уравнений с несколькими неизвестными и с целыми коэффициентами в целых числах.

Доказано, что такого алгоритма не существует (Ю В. Матиясевич, 1970).

3.Построить пример непрерывной функции трех переменных, которая не представима в виде суперпозиции непрерывных функций двух переменных. Смысл это проблемы: функция трех переменных в принципе устроена сложнее, чем функция двух переменных.

Решение проблемы оказалось также отрицательным: с помощью одной функции двух переменных и непрерывных функций одной переменной можно построить любую непрерывную функциюпеременных, где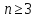(А.Н. Колмогоров, В.И. Арнольд, 1957).

4.Доказать, что любое число вида 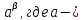алгебраическое число, отличное от 0 и 1,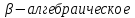число не ниже второй степени, есть число−трансцендентное. (Степенью алгебраического числа называется степень многочлена с рациональными коэффициентами, корнем которого оно является. Допускаются мнимые значения).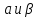

Это предложение доказано А.О. Гельфандом и Т. Шнейдером в 1934г.

В первой половине XX в. математика в значительной степени развивалась под влиянием проблем Гильберта. К настоящему времени большинство проблем решены.

В двадцатые годы XX в. Гильберт и ряд его последователей задались целью перестроить всю математику на аксиоматической основе. Они надеялись на этом пути решить все главные проблемы основания математики. однако результаты австрийского математика К. Геделя, полученные в начале тридцатых годов, привели к краху эту программу. Гедель с помощью математической логики доказал следующее: любая непротиворечивая формализация 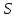арифметики или любой другой теории, содержащей арифметику (например, теории множеств) неполна: в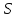имеются неразрешимые формулы, т.е. 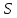такие, которые нельзя ни доказать, ни опровергнуть с помощью конечного числа рассуждений в рамках этой теории; такая формализация непополнима: каким бы конечным множеством дополнительных аксиом ни решить систему, в новой формальной системе существуют свои неразрешимые формулы. Эту теорему Геделя по праву можно назвать великой: она ставит принципиальные границы для полной формализации большей части математики – той, которая пользуется арифметикой можно назвать великой: она ставит принципиальные границы для полной формализации большей части математики – той, которая пользуется арифметикой. Алгоритмически неразрешимые формулы были обнаружены во многих разделах математики: в теории множеств (гипотеза континуума), алгебре, теории чисел, топологии, теории вероятностей и др.