§ 3. Математика древнего Египта

В IV-I тысячелетиях до н. э. в странах древнего Востока. Устанавливается рабовладельческий строй. Рабовладельческий строй давал возможность вести большие строительные работы, совершенствовать орудия труда, развивать ремесла и торговлю, однако производительные силы общества развивались медленно, поскольку рабы не были заинтересованы в повышении производительности своего труда и господствовал примитивный ручной труд. наиболее крупными и значительными среди первых рабовладельческих государств были Египет, Вавилон, государства в Индии и Китае.

С древнейших времен люди на Востоке селились по долинам крупных рек. Одним из таких районов была долина Нила. В IV тысячелетии до н.э. с развитием земледелия, ремесел и обмена, с появлением неравенства между людьми здесь формируется рабовладельческий строй. Образуются два царства – Верхнее и Нижнее. Около 2700 г. до н.э. они сливаются в единое египетское царство. Оно просуществовало, с некоторыми перерывами, до 525 г. до н.э., когда его завоевали персы.

В Египте строили большие здания (дворцы и храмы), крепости, корабли, оросительные каналы и гробницы-пирамиды. Кроме того, нужно было измерять длины, площади, объемы, время, считать и собирать налоги, составлять календарь и т.д. Все это требовало вычислений и расчетов, т.е. помощи математики.

Египтяне писали на папирусе – бумаге, склеенной из высушенных стеблей водного растения, называвшегося также папирусом. Эту бумагу скатывали в виде свитка, порой довольно значительной длины. Материал был недолговечен, и только благодаря тому, что в Египте было принято класть папирусы в пирамиды знатных людей, часть исписанных папирусов сохранилась до наших дней. Наиболее крупными среди папирусов математического содержания являются папирус Ринда, который содержит 84 решенных задачи, и московский папирус, в котором 25 задач.

Письма и приказы фараона составляли царские писцы, они же вели математические расчеты и вычисления. Большинство папирусов математического содержания были сборниками задач для школ писцов.

Арифметика. В Египте в различные периоды применялись три разных вида письменности. Соответственно этому существовали три вида записи чисел. Рассмотрим примеры записи натуральных чисел в наиболее древней системе счисления – иероглифической (т.е. рисуночный) (рис.1).

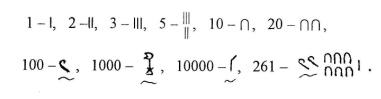
Рис.1

По своему типу эта система, как и две другие, была десятичной и притом непозиционной, поскольку, например, в записи ∩∩∩ значение каждого знака не зависело от его места, позиции. В основании подобных систем счисления лежит аддитивный принцип – когда при записи натурального числа несколькими основными знаками (цифрами), стоящими рядом, подразумевается сложение этих знаков.

Интересно, что знак для единицы, как и во всех древнейших системах, произошел от вида зарубки на кости, камне или дереве, с помощью которой первобытный человек фиксировал результат счета, или от вида мерной палки. Знаки для 10, 100, 1000, 10000 при письме представляли собой иероглифы, обозначавшие соответственно путы для стреноживания коров, мерную веревку, цветок лотоса, указательный палец.

Знаков действий и знака равенства не было, вместо этого указывали словесно, какое действие производится.

Как выполнялись действия над натуральными числами? Сложение и вычитание, по-видимому, - с помощью перекладывания камешков; на папирусе фиксировался лишь полученный результат. Своеобразно, с помощью последовательного удвоения производилось умножение.

Пример 1. 12 умножить на 12.

В папирусе мы находим только следующие записи:

1. 12

2 24

1 4 48

Очевидно, здесь имелись в виду такие вычисления:

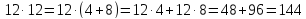
При этом числа 24, 48 и 96 получались с помощью удвоения предыдущих чисел из того же столбца.

Иногда для ускорения умножения применялось, кроме удвоения, еще и удесятирение (и даже упятирение).

Деление понималось и производилось, как действие, обратное умножению.

Пример 2. 1120 разделить на 80.

В папирусе имеются следующие записи:

1 80 I 10 800 2 160 I 4 320 Всего 1120..

Действительным результатом здесь является не 1120 = 800 + 320, а 10 + 4=14. Имеются в виду такие вычисления:

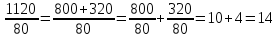
В тех случаях, когда деление “не выходило”, приходилось прибегать к дробям. Египтяне знали только так называемые “основные” дроби (доли единицы), т.е. дроби с числителем, равным 1. Для таких дробей имелось универсальное обозначение: знак части под которым писали знаменатель дроби. Например, 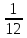записывалась как∩ II и называлась “двенадцатой частью”. Кроме того,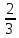имели свой собственный знакII .

На практике должны были часто встречаться неосновные дроби: 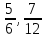и др. У египтян существовали специальные таблицы представления неосновных дробей в виде суммы основных, например:

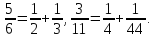
Кроме того, имелись таблицы представления суммы двух равных основных дробей в виде суммы различных основных дробей, например:

.

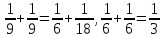С помощью этих таблиц производилось сложение и вычитание дробей, что касается умножения и деления, то в текстах встречаются лишь их простейшие случаи.

Какие арифметические задачи решались в Египте? Это были несложные задачи практического характера: на подсчет количества зерна, необходимого для приготовления данного количества хлеба или пива, на подсчет количества корма для животных, на перевод мер площади или объема в другие единицы и т.д. при решении широко использовалась пропорциональная зависимость между величинами.

Геометрия. Вычисление площадей и объемов, составление планов строений в Египте производили царские писцы. Построениями на местности занимались специальные землемеры. основным инструментом землемера была мерная веревка – веревка, на которой были завязаны узелки на расстоянии друг от друга, равном единице длины. С помощью этой веревки измеряли расстояния, проводили прямые, описывали окружности и даже строили прямые углы на местности. Построение прямого угла было основано на том факте, что треугольник со сторонами длины 3, 4 и 5 является прямоугольным. Этот треугольник в истории получил название египетского. Что касается теоремы Пифагора, то она, по-видимому, египтянам была неизвестна.

Египтяне знали верные правила вычисления площадей прямоугольников, треугольников и трапеций. Площадь выпуклого четырехугольника с последовательными сторонами 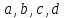вычислялась по неверной формулеS=∙.

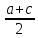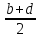Площадь круга приравнивалась площади квадрата со стороной, составляющей 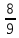диаметра: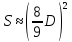. Интересно вывести отсюда, каким приближенным значением числа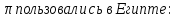

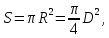
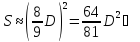
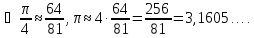
Это хорошее приближение для .

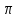Египтяне правильно вычисляли объемы прямого параллелепипеда, прямой, призмы, цилиндра.

Вероятно, большинство правил вычисления площадей и объемов было получено опытным путем. Исключением является верная формула объема правильной четырехугольной усеченной пирамиды

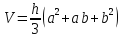
( - стороны оснований,высота пирамиды), которую можно было получить только с помощью логических рассуждений. Не ясно, как она была выведена.

Алгебра. В древнем Египте владели в неявной форме понятиями уравнения и неизвестного и умели решать задачи на уравнения первой степени и простейшие уравнения второй степени с одним неизвестным. Неизвестное называлось “аха” – куча, груда (в смысле – количество, множество), а задачи на уравнения первой степени назывались задачами “аха”.

Пример 3. Количество и его четвертая часть дают вместе 15’’ .

Задача сводится к решению уравнения

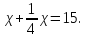
Решается она так. Предположим, что количество равно 4. тогда его четвертая часть равна 1, а количество вместе с четвертой частью (а не 15). Но так как 15 больше 5 в 3 раза, то и количество больше 4 в 3 раза, т.е. равно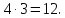

Примененный здесь способ решения в средние века получил название метода ложного положения. При решении использовалась пропорциональная зависимость.

Обращает на себя внимание, что задачи “аха” не были конкретными практическими задачами, они являлись уже элементом отвлеченного математического мышления.

В папирусах можно также найти немногочисленные задачи на арифметическую и геометрическую прогрессии.

В целом уровень египетской математики был довольно низким. математика в древнем Египте еще не была настоящей наукой, а скорее собранием правил и формул, полученных, в основном, опытным путем. Доказательств в явной форме нет. обучение математике было догматическим; при решении задач просто следовали имеющимся образцам. Тем не менее египетская математика оказала значительное влияние на математические знания соседних народов, особенно Греции. Греки считали, что геометрия впервые появилась в Египте.