§ 27. Последующие предшественники интегрального исчисления

К последующим предшественникам интегрального исчисления относятся ученые, работающие во второй половине XVII в. до появления в печати первых работ Лейбница по дифференциальному и интегральному исчислению, -П. Ферма, Б. Паскаль, Д. Валлис и др. Формально все они оставались в рамках метода неделимых, но стремились объяснить, как следует понимать его язык. Вместо сумм неделимых Кавальери они рассматривали или суммы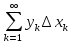(используя бесконечные ряды), или даже интегральные суммы

с конечным числом слагаемых . Предельный переход отчетливо заметен только у Валлиса. В первую очередь, были известны работы. Б.Паскаля и П. Ферма по вычислению площадей и объемов ввиду авторитета, которым пользовались эти ученые в научных кругах, но по-видимому, еще большего внимания, чем это случилось в действительности, заслуживали результаты Валлиса. Приведем примеры из работы « Арифметические исследования» этого английского ученого, опубликованной в 1656 г.

Пример 1. Найти площадь фигуры, ограниченной линиями

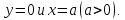
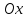Разделим отрезок осинаn равных частей и через точки деления проведем прямые, параллельные оси 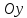(рис. 39).

Тогда на основании основного положения теории неделимых площади фигур ОВС и OABC относятся (приближенно), как суммы неделимых этих фигур, проведенных через точки деления оси :

Последнее выражение при 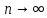стремится к. Валлис, не зная теорем о пределах, догадывается об этом, подаваяn значения 1,2,3,4,5,6. Теперь получаем точную формулу

откуда

Этот результат фактически означает следующее:

Пример 2. Найти площадь фигуры, ограниченной линиями

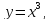
Аналогичным способом Валлис получает, что площадь такой фигуры

,

а это равносильно формуле

Пример 3. Найти площадь фигуры, ограниченной линиями

),

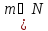Валлис приводит соответствующие формулы без доказательства, пользуясь неполной индукцией:

Для нас она означает следующее:

Найдем еще площадь фигуры OAB:

Пример 4. Вычислить площадь фигуры, ограниченной линиями

(рис. 41).

Валлис проектирует соответствующую фигуру OBC не на ось Ox, а на ось Oy, т.е. заменяет уравнение на уравнениеа отрезокосиOx− на отрезок осиOy. Тогда, по предыдущему (см. пример 3), получаем:

Этот результат равносилен формуле

Наконец, на примерах Валлис обобщает выведенные формулы на степени с любым положительным рациональным показателем.

§ 28. Предшественники дифференциального исчисления

Первым предшественником дифференциального исчисления был Архимед. Однако дифференциальных методов в работах Архимеда было немного, и они не были замечены ни в Греции, ни в средние века, ни, наконец, в XVII в. Поэтому ученые XVII в., решая задачи дифференциального исчисления, вынуждены были начать с нуля. В XVII в. задачами дифференциального исчисления занимались П. Ферма, Б. Паскаль, Ж. Роберваль, Е. Торричелли, И. Барроу и др.

П. Ферма один из первых стал находить экстремумы величин. Этому вопросу посвящена его работа « Метод отыскания наибольших и наименьших значений» (число опубликовано в 1642−1644 гг., а полностью – после смерти автора в 1679 г.). Задачу нахождения экстремума он решает на примерах, но общим методом.

Пример. Данный отрезок 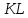рассечь точкой на такие два отрезка, чтобы прямоугольный параллелепипед, построенный на квадратебыл наибольшим.

Положим

(напомним, что это символика Виета – гласными буквами). Тогда объем параллелепипеда

Теперь Ферма дает переменной приращениеи находит новое значение объема:

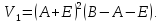
Приравняем (приближенно) эти значения объема:

После сокращения на получим:

В последнем равенстве Ферма полагает 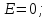после этого будем иметь, по его мнению, точное равенство:

Фактически здесь использовался принцип пренебрежения бесконечно малыми высших порядков: отбрасываются те члены первоначального равенства, которые содержат бесконечно малую во второй или третьей степени. Этот принцип был хорошо известен и широко применялся вXVII в.

Теперь разберемся в выкладках Ферма с точки зрения современного дифференциального исчисления. Положим Тогда

Так как в случае, когда есть многочлен, полагатьравносильно тому, чтостремится к нулю, то последнее равенство можно заменить следующим:

Мы получим необходимый признак экстремума Ферма: в точке экстремума дифференцируемой функции ее производная обращается в нуль. Но его обоснования автор не дал. Нет у него и достаточного признака экстремума.

Метод Ферма решения задач на экстремум пользовался известностью в Западной Европе под названием «метода наибольших и наименьших». Но некоторые ученые указывали на его противоречивость: с одной стороны, автор сокращает равенство на бесконечно малую и, следовательно, считает, чтоа с другой – после этого полагает

Похожим методом Ферма строит касательные к кривым. Он демонстрирует его также только на примерах, но мы рассмотрим сразу общий случай, сохраняя идею автора.

Пусть кривая задана уравнением Положимподкасательная к кривой (рис. 42). Очевидно, построение касательнойк построению подкасательнойт.е. к нахождению точки

Дадим переменной приращениеи положим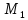𝒬=J

Треугольники (где треугольник− криволинейный) приближенно подобны. Тогда

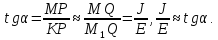
В последнем равенстве положим получаем, по мнению Ферма, точное равенство:

С нашей точки зрения это означает следующее:

где абсцисса точки

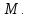
Рассмотрим еще результаты Барроу. Исаак Барроу (1630−1677) окончил университет в Кембридже (Англия) и там же преподавал. Среди его университетских учебников был Ньютон. В 1669−1670 гг. Барроу издал «Лекции по оптике и геометрии». В этих лекциях он, в частности, строит касательные к кривым методом, близким к методу Ферма. Остановимся на двух важных задачах, которые Барроу решает в своих лекциях:

1. как, зная касательную к кривой, найти площадь криволинейной трапеции, находящееся под этой кривой;

2. как, зная площадь криволинейной трапеции, находящейся под кривой, построить касательную к кривой.

По существу, здесь речь идет о взаимной обратности операции дифференцирования и интегрирования, но без современных терминов и символики, а кроме того, в геометрической форме. К тому же у Барроу эти задачи отделены друг от друга большим числом теорем, не сопоставлены между собой и в дальнейшем почти не используются.