§ 26. Первые предшественники интегрального исчисления

Первым предшественником интегрального исчисления был Архимед, греческий ученый III в. до н. э. Ученые XVII в. использовали многие его идеи, но метод исчерпывания, который он применял, стремились упростить. В XVII в. успеха в решении задач по вычислению площадей и объемов добивались те ученые, которые пользовались нестрогими методами, быстрее приводившими к цели.

Одним из первых был немецкий астроном и математик Иоганн Кеплер. В 1615 г. он опубликовал сочинение « Новая стереометрия винных бочек». Название труда связано с тем, что Кеплер наблюдал, как измеряют объем винной бочки австрийские виноделы, пользуясь одним - единственным измерением – по диагонали бочки; затем применялось правила, полученное опытным путем. Кеплер заинтересовался этим правилом и оценил его точность; она оказалась довольно высокой. Но для него решение указанной задачи было лишь поводом для перехода к более серьезным вопросам.

Он выводит формулу площади круга и формулы объемов тел, которые встречались еще у Архимеда, а также большое количество формула объемов, которых у Архимеда нет.

Для вычисления площади круга Кеплер разбивает круг на бесконечное множество секторов, каждый из которых он рассматривает как треугольник с основанием, равным длине 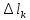соответствующей дуги окружности, и высотой, равной радиусуR .Тогда площадь круга равна

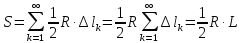
где L− длина окружности.

Рассмотрим еще вывод формулы объема тора – тела, образованного при вращении круга вокруг оси, лежащей в плоскости круга и не имеющей с ним общих точек (рис. 37). Кеплер разбивает тор на бесконечное множество тонких слоев плоскостями, проходящими через ось вращения, и каждый такой слой считает цилиндром с радиусом основании, равным радиусу R вращающегося

круга, и высотой, равной дуге 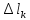окружности,

описанной центром этого круга при вращении.

Тогда объем тора равен

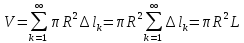
Получилась верная формула, хотя и выведенная, с современной точки зрения, нестрогим путем.

Фактически Кеплер при выводе формул объемов как сумму бесконечного множества бесконечно малых слагаемых. Но вычисление такой суммы он в каждом конкретном случае производит по-разному, так как никаких общих теорем у него нет.

Продолжателем идей Кеплера был итальянский ученый Бонавентура Кавальери (ок. 1596-1647). Он был монахом, но больше всего занимался математикой, а к концу жизни стал профессором математики в Болонье. Кавальери разработал общий метод вычисления площадей и объемов – метод неделимых, и пропаганда этого метода стала для него главным делом жизни. В 1635 г. он издал свой основной труд « Геометрия, развитая новым способом при помощи неделимых непрерывного», а в 1647 г. его предложение « Шесть геометрических этюдов».

В отличие от Кеплера, Кавальери сначала доказывает общие предложения и лишь потом применяет их к вычислению конкретных площадей и объемов.

Для плоской фигуры Кавальери проводит в ней всевозможные отрезки, параллельные некоторой прямой (рис. 38). Эти отрезки и называются неделимыми. Число неделимых бесконечно, и они не имеют толщины.

Аналогично, неделимыми пространственного тела являются куски параллельных плоскостей, где каждый кусок ограничен линией, лежащей на поверхности тела.

Далее он просматривает суммы всех неделимых данной фигуры (или тела)

Они похожи на современные интегральные суммы

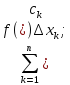
отличия в том, что число слагаемых в сумме неделимых бесконечно, а кроме того, слагаемые не содержат множителей

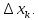
Кавальери не утверждает, что площадь плоской фигуры равна сумме ее неделимых

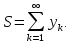
Дело в том, что сумма неделимых состоит из бесконечного множества слагаемых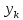, не являющихся бесконечно малыми, а следовательно, есть бесконечно большая величина. Основное положение теории неделимых, которое автор приводит с доказательством, формулируется осторожнее: две фигуры (или два тела) относятся, как суммы их неделимых

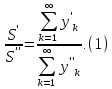Отношение двух бесконечно больших в правой части равенства (1) уже могло быть конечной величиной.

Равенство (1) с современной точки зрения означает, что

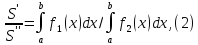
но равенство (2) не равносильно равенству

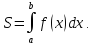
Далее Кавальери фактически доказал, что

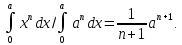
при n=1,2,3 ,а позднее при n=4,5,…9 , распространив полученные формулы по не полной индукции на степенную функцию с любым натуральным показателем.

Из основного положения теории неделимых автор выводит так называемый принцип Кавальери, который в случае объемов тел формулируется следующим образом: если два тела имеют одну и ту же высоту и сечения этих тел плоскостями, проведенными, на одной и той же высоте, равны. то и сами тела равны. Действительно, так как при любом натуральном k не делимые суммы равны: 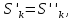то для объемов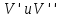этих тел получаем:

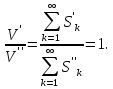
Только теперь, пользуясь доказательными формулами, Кавальери приступает к геометрическим приложениям своего метода: к квадратуре параболы 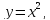спирали Архимеда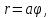к кубатуре пирамиды и многих других тел.

Метод неделимых завоевал известность в Западной Европе, и его применяли многие ученые. Но все же он был слишком громоздок, отчасти потому, что Кавальери не пользовался алгебраической символикой, а свои предложения и их доказательства излагал в словесной форме. Неясным оставался математический смысл понятий неделимого и суммы неделимых. Метод нельзя было применять к вычислению кривых, так как в этом случае неделимой является точка, т.е. безразмерная величина; между тем, решение задач на вычисление длин кривых в ряде случаев вызывалось теоретической или практической необходимостью.