§ 25. Создание основ аналитической геометрии

1.XVII и XVIII века называют Новым временем.

В Западной Европе утверждается капитализм после буржуазных революций, продолжавшихся два с половиной столетия, − от революций в странах Центральной Европы в середине XIX в.

Новое время было и эпохой научной революции. Гелиоцентрическая система строения мира Коперника, законы движения планет Кеплера, динамика Галилея, окончательно разработанная Ньютоном, открытия в оптике (Ньютон и Гук) – вот основные научные открытия в механике, физике и астрономии. Особая роль отводилась механике, которая по мнению ученых того времени, должна была дать полную картину физического строения реального мира. При этом механика не могла обойтись без весьма существенной помощи математики.

Математика получает множество стимулов для своего развития. Великие географические открытия и создание гелиоцентрической системы строения Вселенной оживили занятия – переход от мануфактурной промышленности к фабричной, делается большое количество технических изобретений, среди которых наиболее важным было создание паровой машины. Все это вызвало бурное развитие техники и различных областей механики. В математике первостепенную роль стали играть вопросы прикладного характера, поставленные перед нею техникой и естествознанием. Математик зачастую был одновременно механиком, астрономом, инженером или философом. Новые задачи, возникшие перед математикой, большей частью не могли быть решены старыми средствами, а требовали для своего решения, как это стало вполне ясным лишь в XIX в., идеи переменной величины и аппарата теории пределов.

XVII−XVIII вв. образуют новый, третий период истории математики – период математики переменных величин. Главным приобретением науки этого времени является анализ бесконечно малых, а также тесно связанная с ним аналитическая геометрия. Кроме того, появляются теория вероятностей, проективная геометрия, теория чисел. Создание математического анализа и аналитической геометрии произвело подлинную революцию в математике, так как ввело в нее совершенно новые понятия и методы .

В XVII в. на первый план в математике и вообще в науке выдвигаются передовые в социальном и экономическом отношении страны − Англия, Франция и Голландия. Создаются научные общества и академии, появляются первые научные периодические издания, пока немногочисленные. В условиях, когда периодических изданий почти не было, а издание научных книг было и долгим, и дорогостоящим делом, большую роль в развитии науки играли ученые – распространители информации. Во Франции эту функцию выполнял М. Мерсенн, который вел оживленную переписку с Декартом, Ферма, Галилеем и другими учеными. Благодаря Марсенну научные результаты, полученные, например, Ферма, становились известными, разумеется, не всем ученым, а тем, кто занимался вопросами, близкими к проблематике Ферма, задолго до публикации этих результатов в книгах или статьях.

Обратимся непосредственно к теме параграфа.

Координаты появились еще в древней Греции: географические, астрономические и, главное, те, которые использовались учеными, прежде всего, Аполлонием, при построении теории конических сечений. В последнем случае строилась весьма подробная, систематически изложенная теория («Конические сечения» Аполлония), однако ее крупным недостатком было отсутствие алгебраической символики, что вынуждало автора пользоваться геометрической алгеброй из «Начал» Евклида, а следовательно, стремиться к тому, чтобы в уравнении кривой все члены имели одну и ту же степень (принцип однородности). Ясно, что и доказательства свойств конических сечений получались большей частью сложными и длинными.

Основы аналитической геометрии на плоскости заложили в XVII в. два французских ученых Декарт и Ферма.

2. Пьер Ферма (1601-1665) окончил юридический факультет университета в г. Тулузе на юге Франции, всю жизнь жил в Тулузе, где служил юристом, советником местных органов управления. Имея мало времени для научных занятий, он тем не менее получил первоклассные результаты в дифференциальном и интегральном исчислении, аналитической геометрии, теории чисел и теории вероятностей.

Аналитической геометрии Ферма посвятил небольшое сочинение «Введение в теорию плоских и пространственных мест». Это сочинение стало известным в рукописном виде при содействии Мерсенна с 1636 г., главным образом, во Франции, но опубликовано было, как и большинство работ Ферма по математике, намного позже, после его смерти,

в 1679г.

У Ферма имеется только одна координатная ось − ось абсцисс, точнее, полуось, так как отрицательными координатами он не пользуется; для изображения значений другой переменной он из конца отрезка оси абсцисс проводил отрезки под некоторым постоянным углом к этой оси, вообще говоря, не прямым.

Уравнение прямой, проходящей через начальную точку, Ферма пишет в виде

D на A равно B на E,

т.е. (он пользовался не удобной символикой Виета). Уравнение Ферма преобразует, полагая

и пользуясь далее параллельным сдвигом вдоль оси абсцисс. Он выводит уравнение окружности с центром в начальной точке в виде , а затем приводит к этому виду уравнение:

,

,

где . Фактически и здесь используется преобразование системы координат – идея, которую Ферма широко применял.

Уравнение конических сечений он пишет, выражая их свойства из труда Аполлония на языке алгебры: для параболы 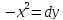или, для эллипса(гдеC – постоянная), для гиперболы для равносторонней гиперболы

3.Рене Декарт (1596 – 1650) происходил из дворянской семьи. Получил хорошее образование в иезуитском колледже. Но в математике был самоучкой, как и ферма. В Париже сблизился с Мерсенном. Затем участвовал в 30-летней войне и в войне с гугенотами. Наконец, Декарт полностью перешел к научным занятиям.

Прежде все он занялся философией. Декарт считал, что знание должно быть основано на разуме, дедуктивных рассуждениях, а не на догмах средневековой схоластики. Этим он вызвал недовольство католической церкви. Тогда Декарт переехал в Голландию и прожил там около двадцати лет, целиком занятый наукой. Впрочем, его философские взгляды вызвали в Голландии и недовольство протестантской церкви. В 1637 г. Декарт издал сочинение « Рассуждение о методе», в котором изложил свою философию.

Его философия была дуалистической: она признавала существование двух самостоятельных субстанций – материи и духа. Но в своих занятиях физикой Декарт показал себя материалистом, причем материалистом механистическим.

К своей главной работе он приложил три отдельных сочинения –«Диоптрика» (оптика), «Метеоры» (физика Земли и атмосферы) и «Геометрия» (аналитическая геометрия). Декарт этими сочинениями стремился показать, как преломляется его философия в конкретных науках. Наибольшую известность получила последняя работа.

В 1649 г. Декарт переехал в Швецию, но через год умер, заболев воспалением легких.

Декарт искал общий метод мышления, который позволил бы быстрее находить истину в различных науках. Поскольку единственной наукой о природе, обладавшей в известной мере систематическим строением, была тогда механика, а ключ к пониманию механики давала математика, то математика стала для Декарта наиболее важным средством для изучения природы. Он стремился разобрать общий дедуктивно-математический метод исследования всех вопросов естествознания. Конкретным орудием наук о природе должна была стать некоторая новая математика, которую он назвал всеобщей.

«Геометрия» состоит из трех книг. Вопросы аналитической геометрии в ней разбросаны без особой системы по всем трем книгам. В этом отношении она уступает сочинению Ферма. Однако, «Геометрия» пользовалась гораздо большей известностью среди ученых. Во-первых, она была напечатана - гораздо раньше, чем работа Ферма. Во-вторых, в ней использовалась более совершенная алгебраическая символика, большая часть которой была придумана самим Декартом (см. § 21, п.4). Главное же – она гораздо богаче идеями и насыщена примерами. В основу «Геометрии» положены две идеи: решение геометрических задач с помощью алгебры и метода координат и понятие переменной величины. «Поворотным пунктом в математике была декартова переменная величина. Благодаря этому в математику вошли движение и тем самым диалектика» - написал Ф. Энгельс в работе «Диалектика природы».

Декарт подобно Ферма, чертил только одну координатную ось с начальной точкой, указывая направления других координат точек. Но иногда он проводил и две координатные оси, правда, располагая их необычным для нас образом. Кроме того, он, и Ферма, почти не употреблял отрицательных координат, что вынуждало его обрывать кривую точками, лежащими на координатных осях (рис.35).

Декарт считал, что в геометрии нужно пользоваться, главным образом, линиями, образованными кинематически, т. е. такими, которые описаны непрерывным движением или несколькими такими последовательными движениями. При записи уравнений линий он делает важный шаг вперед, отказавшись от принципа однородности, которого придерживался Виет и даже Ферма. Например, если нужно было построить отрезок, гдеданный отрезок, то, записав это равенство в виде, Декарт находит отрезок, как четвертый пропорциональный к тем данным отрезкам:; если нужно было построить отрезокприведя последнее равенство к виду, он находиттаким же построением:. Это позволило Декарту установить взаимно однозначное соответствие между алгебраическими углы взяты для уравнениямигде члены многочленаимеют, вообще говоря, разную степень, и изображающими их линиями на плоскости.

Для того чтобы продемонстрировать мощь нового метода решения геометрических задач, Декарт, в частности, решает трудную задачу, сформулированную древнегреческим ученым Паппом: на плоскости даны 2n или 2n-1 прямых, имеет данное отношение к произведению отрезков, проведенных из M под теми же углами к остальным n или прямым:

(рис. 36). (На рисунке указанные в условии определенности прямыми.)

При решении этой задачи Декарт пользуется косоугольными координатами. Ответом является кривая порядка n. Более подробно Декарт рассмотрел случаи Приполучается кривая второго порядка, причем он выяснил, когда получаются эллипс, парабола, гипербола или прямая. Третья книга «Геометрии» посвящена, в основном, алгебре. В частности, в ней вводятся обозначения известных и неизвестных величин, а также обозначения степеней, которыми мы пользуемся и сейчас, формулируются несколько теорем алгебры (см. § 21).

4.Последователи Декарта в XVII в. стремились систематизировать его аналитическую геометрию, рассматривая уравнения прямой, конических сечений, уравнения алгебраических кривых степеней выше второй степени и др. Отметим работу И.Ньютона « Перечисление кривых третьего порядка» (написанную еще в 60-е годы XVII в., но опубликованную лишь в 1704 г.). В ней Ньютон впервые дает классификацию алгебраических кривых по степени соответствующих уравнений. У него система координат (прямоугольных и косоугольных) уже ничем не отличается от современной . Он обобщает на кривые третьего порядка понятия диаметра, оси, центра, вершины и делит кривые третьего порядка на 72 вида, сводя их к четырем основным типам. Предложения о таких кривых Ньютон, как правило, приводит без доказательств. В 1729 г. французский ученый А.Клеро в своей книге « Исследование о кривых двоякой кривизны» распространил аналитическую и дифференциальную геометрию с плоскости на пространство.

Ведущей фигурой здесь выступил знаменитый математик XVIII в. Л. Эйлер. В. 1748 г. он опубликовал большое сочинение «Введение в анализ бесконечных» в двух томах, из которых первый том посвящен введению в анализ, а второй – аналитической геометрии. Рассмотрим прямоугольные и косоугольные координаты точки на плоскости и рассматривается деление алгебраических кривых на порядки в зависимости от степени уравнений. Для изучения таких кривых широко используются формулы преобразования системы координат. Эйлер подробно излагает общую теорию кривых второго порядка, деля эти кривые на типы и приводя их уравнения к каноническим. Он изучает также кривые третьего порядка, деля их на 16 родов, и кривые четвертого порядка (146 родов). Затем автор вводит координаты в пространстве и рассматривает уравнения поверхностей в пространстве, исследует общее уравнение поверхности второго порядка, приводя его к каноническим уравнениям поверхностей. Довольно кратко он рассматривает пространственные кривые, представляя их как пересечения двух поверхностей. В основном Эйлер завершил работу систематизации аналитической геометрии. Некоторые его результаты, относящиеся к пространству, были развиты другими учеными XVIII в.