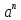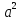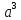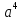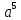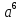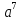§ 24. Составление таблиц логарифмов

В конце XVI – начале XVII вв. резко возрос объем вычислений, которые приходилось проводить ученым. Это было связано прежде всего с потребностями астрономии и тригонометрии, а также финансового и торгового дела, а с развитием анализа бесконечно малых – и с необходимостью решения задач анализа. Дело упиралось в несовершенство вычислительной техники того времени. В частности чувствовалась необходимость в изобретении десятичных дробей. Десятичные дроби впервые ввел один из арабских ученых – ал-Каши еще в XV в., но его открытие осталось незамеченным.

В западной Европе десятичные дроби открыл голландский инженер и математик Симон Стевин. В 1585 г. он издал маленькую, всего в 7 страниц, работу «Десятая», посвященную десятичным дробям. При этом он применял своеобразные обозначения; например, дробь 5,912 он записывал следующим образом:

5 9 1 2

1

2

3

0

Очевидно, здесь в кружках записаны номера разрядов соответствующих цифр.

Несколько позднее десятичные дроби стали записывать привычным для нас способом. При этом для отделения целой части числа от дробной известный немецкий астроном и математик Кеплер ввел запятую, а английский ученый Джон Непер – точку. Точка при записи десятичных дробей и сейчас употребляется в англоязычных странах. Десятичные дроби стали использоваться при составлении тригонометрических таблиц и таблиц логарифмов.

В XVI в. идея логарифма носилась в воздухе. Она выражалась в сопоставлении членов арифметической и геометрической прогрессий. Рассмотрим таблицу значений степени 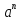(табл. 2).

n	1	2	3	4	5	6	7	…
	a							…

Табл. 2

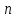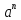Когда показатель пробегает арифметическую прогрессию, степеньпробегает геометрическую прогрессию. С современной точки зренияНесколько ученых заметили, что с помощью таких таблиц можно упрощать вычисления: умножению и делению членов геометрической прогрессии, иными словами, умножение и деление нижней строки можно заменить сложением и вычитанием соответствующих чисел верхней строки; возведению в степень и извлечению корня в геометрической прогрессии отвечают умножение и деление в арифметической прогрессии. Очевидно, это зародыш идеи логарифма; в частности, здесь запрятаны свойства логарифма произведения, частного, степени и корня.

Подобные идеи выражали французский ученый Николь Орем еще в конце XIV в., французский математик Никола Шюке в конце XV в. и особенно немецкий ученый из школы коссистов Михаэль Штифель в середине XVI в.

Стремление расширить таблицы значений степени на случай, когда показательn принимает не только натуральные значения, значительно способствовало формированию в XIV – XVII вв. понятий о степени с нулевым, целым отрицательным и дробным показателем.

На первых порах проблема была в том, какое число взять в качестве основания степени , т.е. в качестве знаменателя геометрической прогрессии. Дело в том, что, например, при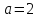и тем более при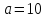эта степень с возрастаниемn растет слишком быстро, что не позволяло включить в геометрическую прогрессию многие числа. Поэтому на первых порах приходилось в качестве 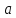брать число, близкое к 1: в этом случае степень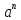с возрастанием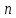изменяется гораздо медленнее.

Первые таблицы логарифмов составили независимо друг от друга английский ученый Д. Непер и швейцарский математик И. Бюрги.

Иост Бюрги был часовым дел мастером в Праге, позднее работал вместе с Кеплером, помогал ему в составлении астрономических таблиц. В 1620 г. он издал сочинение «Таблицы арифметической и геометрической прогрессии».

Бюрги выбрал знаменатель геометрической прогрессии равным 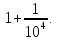Члены геометрической прогрессии он умножал на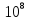, для того, чтобы возможно дольше избегать дробей, а члены арифметической прогрессии – на 10. Получается, что члены арифметической прогрессии имеют вид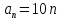, а члены геометрической прогрессии – вид.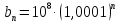

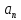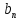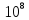Числа не являются логарифмами чисел, но если разделить члены геометрической прогрессии Бюрги на, а члены арифметической прогрессии – на 10, то получатся логарифмы по основанию