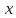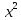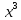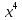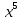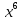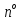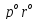§ 21. Создание алгебраической символики

В XV-XVI вв. наибольших успехов ученые Западной Европы достигли в области алгебры. Развитие алгебры в сильной степени тормозилось отсутствием алгебраической символики. Создание символики в XV-XVII вв. означало не только изменение формы выражения для уже известных тождеств и управлений, но и позволило коренным образом преобразовать всю алгебру, а вместе с ней существенно изменило и всю математику. Вспомним, что в XVII в. начинается новый, третий период истории математики.

1. Крупнейшим европейским алгебраистом XV в. был итальянец Лука Пачоли ( ок1445-ок. 1515). Он был монахом и профессором математики в университетах нескольких итальянских городов. Его главный труд – « Сумма (знаний) по арифметике, геометрии, отношениям и пропорциональности» вышел в 1494 г. и написан на итальянском языке, что было тогда редкостью. Это энциклопедия математических знаний того времени.

В арифметической части книги сравнительно немного нового. Зато при решении уравнений Пачоли вводит алгебраическую символику (рис. 33).

Исходный символ	Символическое обозначение Пачоли	Происхождение символа
α	co ce cu ce.ce. ce.cu.	numero (ит.) – число cosa – вещь censo−квадрат cubo censo de censo primo relato−первое отношен. censo de cubo

Рис.33

Кроме того, квадратный корень он обозначал символом 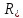(radice-корень) или 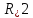, кубический корень –или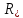cuba, корень четвертой степен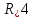и – или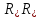. Сложение обозначалось знаком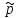(plus), вычитание – знаком 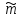(minus).Следовательно, символика Пачоли была синкопированной, так как в ней использовались сокращения соответствующих слов.

Пачоли рассматривает отрицательные числа и правила действий над положительными и отрицательными числами.

Символикой Пачоли широко пользовались итальянские алгебраисты XVI в.

2. Следующий шаг в создании алгебраической символики сделали немецкие ученые XVI в., известные под именем «коссистов». Название объясняется тем, что они именовали алгебру COSS – от итальянского cosa, обозначавшего неизвестное. Крупнейшие коссисты – Видман, Ризе, Рудольф и Штифель.

Так Видман ввел знаки + и −. Ризе и Рудольф вводили следующие обозначения:

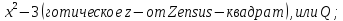
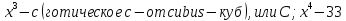и т.д. Свободный член коссисты обозначили знаком ∅.

Самый известный из коссистов – Михаэль Штифель. Это был протестантский пастор, любимым занятием которого было вычисление дат событий, прошлых и будущих, упоминаемых в священных книгах. Например, он предсказал, что 19 октября 1533 г. наступит конец мира. Когда конец мира в этот день не состоялся, Штифель решил заняться математикой всерьез. Он написал две книги «Полная арифметика» (на латинском языке) и «Немецкая арифметика» (на немецком языке). В первой из них он приводит формулу бинома Ньютона для любого натурального показателя в словесной формулировке и таблицу биномиальных коэффициентов, а также рассматривает отрицательные числа и правила действий над положительными и отрицательными числами. Так любое полное квадратное уравнение он записывает в виде, равносильном современной записи 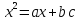любыми по знаку числамиa и b.

Символика коссистов была хорошо известна в Германии.

3. Существенное улучшение в символику внес французский математик Виет.

Франсуа Виет (1540-1603) был юристом и стал советником французского короля. Прославился при дворе тем, что расшифровал переписку испанцев во время войны Франции и Испании за испанское наследство. Написал большое сочинение «Введение в аналитическое искусство», но не успел его завершить.

В уравнениях с буквенными коэффициентами Виет обозначает неизвестные величины гласными буквами: A, E, I,.., а известные − согласными буквами Из знаков действий он употребляет + и −.Так уравнение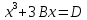он описывает в виде

(aequatur – равно; слова planum и solido означают «площадь» и «тело» и вводились для уравнивания размерности обеих частей уравнения).

Для уравнений с числовыми коэффициентами Виет вводит более простую символику: неизвестное он обозначает через N, квадрат неизвестного – через 𝒬, куб − через C. Например, уравнение 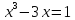он записывает в виде.

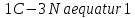Виет сделал первые значительные шаги в построении общей теории алгебраических уравнений. Он известен как один из авторов метода подстановок при решении алгебраических уравнений степени выше второй, изобрел способ приближенного решения алгебраических уравнений. Теорема Виета у него выглядела так: если уравнение 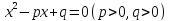имеет корни, то их сумма равнаp, а произведение – q.

Символика Виета широко использовалась не только во Франции, но и в некоторых соседних странах. Но она была еще тяжеловесна.

4. Современную алгебраическую символику ввел французский математик Рене Декарт в его знаменитом сочинении «Геометрия», изданном в 1637 г. Именно он стал впервые обозначать известные величины начальными буквами алфавита a, b, c, …, неизвестные – последними буквами x, y, z. Ему же принадлежат обозначения степеней с натуральными показателями 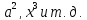Однако современного обозначения степеней с дробными и отрицательными показателями у него нет; их ввел в систематическое употребление И. Ньютон во второй половинеXVII в. Декарт ввел современное обозначение корня; правда, при этом показатель корня он писал не вверху, а под знаком корня перед подкоренным выражением, например, вместо 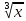он пишет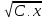. Знак равенства он обозначает символом .

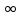Декарт также сформулировал, большей частью доказательства, ряд теорем алгебры:

а) основную теорему алгебры;

б) теорему о том, что корни приведенного кубического уравнения с целыми коэффициентами можно построить циркулем и линейкой тогда и только тогда, когда оно имеет целый корень, т.е. когда оно разлагается на линейное и квадратное с целыми коэффициентами – вопрос, важный, например, для решения задач об удвоении куба и о трисекции угла (см. § 6);

в) если алгебраическое уравнение 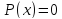имеет корень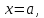то многочислен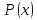делится на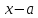и др.

5. Отдельные современные символические обозначения принадлежат следующим ученым.

а) Знак равенства 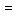ввел английский математик Р. Рекорд в серединеXVI в.

б) Знак умножения 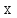впервые встречается у английского математика В. Отреда в серединеXVII в.

в) Знаки умножения и деления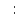ввел немецкий ученый Г. Лейбниц в концеXVII в.

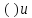
г) Скобки 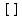изобрели несколько итальянских математиковXVI в.

д) Знаки 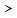иввел английский ученый Т. Гарриот в началеXVII в.

Современная алгебраическая символика завоевывала признание медленно, с трудом. Окончательно она утвердилась в математике Западной Европы лишь в первой половине XVIII в.