§ 18. Математика в арабских странах

В VII в. в Аравии возникла новая религия – ислам, основанная Мухаммедом. Приверженцы этой религии называются мусульманами. Преемники Мухаммеда – халифы принялись покорять неверных и за VII в. завоевали Вавилон, Персию, Египет и весь север Африки. Население этих стран со временем стало считать себя арабами и приверженцами ислама. В VIII – IX вв. арабы проникли на европейский континент и завоевали Испанию и юг Италии, а на востоке – Среднюю Азию, часть Закавказья и Индии. Образовался огромный халифат от Испании на западе до Индии на востоке. Столицей халифата была сначала Дамаск, а затем – новый город Багдад.

Одновременно на территории халифата формируется феодальный строй. Жители халифата занимались земледелием и, следовательно, орошением полей, в Багдаде и других городах ведется большое строительство, развиваются ремесла и торговля. В завоеванных странах халифы обнаружили более высокую культуру и науку, чем в халифате, а поэтому стали вывозить в Багдад ученых, строителей и ремесленников. Арабский язык стал международным языком науки.

К Х в. арабский халифат распадается: завоеванные страны, сохраняя религиозное подчинение Багдаду, во всех других отношениях становятся независимыми. В XI в. арабы были выбиты из Италии, а вот изгнание их из Испании растянулось с Х по XY в.

Сначала наука была сосредоточена в Багдаде, но по мере появления новых арабских государств возникают и новые научные центры. Во многих столицах появляются обсерватории. Широкую известность, в том числе и за пределами арабских стран получили врач Авиценна, или Ибн Сина (Х в.), поэт и одновременно ученый Омар Хайям ( XI – XII вв.), директор Самаркандской обсерватории Улугбек (XV в.). Улугбек был внуком знаменитого среднеазиатского завоевателя Тимура и стал султаном в Самарканде. Но это был странный для того времени султан: он больше был занят наукой и был казнен по тайному приговору церковного суда, члены которого сочли его еретиком.

Математикой, в основном, занимались выходцы из Средней Азии, Персии и Вавилона.

Ученые арабских государств были хорошо знакомы с математикой как Запада, так и Востока, в частности, с индийской математикой. Основные сочинения классиков математики древней Греции: Евклида, Архимеда, Аполлония, Диофанта и др. были переведены на арабский язык. Весьма значительная часть этих сочинений именно поэтому дошла до Западной Европы, когда их стали позднее переводить с арабского на латинский язык.

Арифметика. В Странах ислама применялись два типа нумерации: алфавитная, а следовательно, десятичная непозиционная, и десятичная позиционная, заимствованная у индийцев. В последней применялись цифры, похожие на индийские, с некоторыми отличиями между восточноарабскими и западноарабскими цифрами. Действия над натуральными числами производились на счетной доске, посыпанной песком или пылью, - как в Индии. Из дробей арабские математики знали только обыкновенные дроби, но в астрономии ученые пользовались вавилонскими шестидесятеричными дробями. Дроби большей частью записывали по-индийски: числитель над знаменателем, а целую часть смешанного числа – над числителем. Арифметические задачи решались следующих типов: задачи, возникавшие в торговом деле, при распределении налогов, разделе наследства и др.. При решении использовались пропорциональное деление и тройное правило. Арабы широко пользовались также иррациональными числами.

Алгебра. В алгебре арабские ученые были, в общем, самостоятельны и оригинальны.

Одним из крупнейших арабских математиков был Мухаммед ибн-Муса ал-Хорезми (VIII-IX вв.). Он был узбеком, выходцем из Хорезма, города в Средней Азии, жил и работал в Багдаде. Известен как автор трактата по арифметике, предположительно называвшегося «Книга о сложении и вычитании по исчислению индийцев». По этому сочинению арабы впервые знакомились с индийской десятичной позиционной нумерацией. При переводе его на латинский язык от имени автора образовалось слово «алгоритм», которое первоначально обозначало всю систему десятичной позиционной арифметики.

Но главное сочинение ал-Хорезми посвящено алгебре. Оно носит заглавие « Краткая книга об исчислении ал-джабра и ал-мукабалы». Под «ал-джабром» автор понимает перенос отрицательных членов из одной части уравнения в другую со знаком плюс, а под «ал-мукабалой» - приведение подобных членов в обеих частях уравнения. От слова 2 ал-джабр» произошел современный термин «алгебра».

Алгебраической символики у ал-Хорезми, как и вообще в арабской математике, нет, уравнения читаются словесно. Не были известны и отрицательные уравнения. Он делит эти уравнения на следующие типы:

1)(читается: квадраты равны корням);

2) =c (квадраты равны числу);

3)

4) (квадрат и корни равны числу);

5)

где a,b,c – данные положительные рациональные числа. Для уравнения каждого типа формируется простой алгоритм решения. Обоснование правила дается только x для уравнений четвертого и шестого типов, на примерах, но общим образом. Например, правило решения уравнения 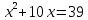доказывается с помощью следующего чертежа (рис. 31).

x

Площадь заштрихованной фигуры равна т.е. 39. Тогда площадь всего большого квадрата равна, с одной стороны,, а с другой - 39 + 25 =64. Получаем:

Фактически это прием выделения полного квадрата в левой части уравнения, только в геометрической форме.

После ал-Хорезми ученые Абу Камил (IX-X вв.) и ал-Кархи (X-XI вв.) изложили решение квадратных уравнений более подробно, в методический обработанном виде, рассмотрели правила тождественных преобразований алгебраических выражений. В частности, у ал-Кархи мы находим суммирование арифметической и геометрической прогрессий, формулы сумм

а также решение трехчленных уравнений.

Ученые арабских стран занялись решением уравнений третьей и четвертой степени. С помощью кубических уравнений они решали задачу о трисекции угла, пришедшую из древней Греции. Постепенно возникла проблема построения общей теории кубических уравнений. С этой проблемой справился Омар Хайям, имя которого упоминалось раньше.

Прежде всего Омар Хайям – знаменитый персидский поэт. Что касается кубических уравнений, то им написан «Трактат о доказательствах задач алджабра». Слово « ал-джабр» он употребляет для названия алгебры и трактует алгебру как самостоятельную науку – науку о решении уравнений. Для решения кубических уравнений он использует геометрию – конические сечения, а име6нно параболу, равностороннюю гиперболу и окружность. В зависимости от решения Хайям делит кубические уравнения на 14 типов. Впрочем, впоследствии оказалось, что его классификация неполна.

Важную роль в арабской математике сыграл ал-Каши ( XIV-XVв..). Главное его сочинение – «Ключ арифметики». Это мастерски написанное руководство по элементарной математике, непревзойденное во всей средневековой литературе по богатству содержания, ясности и четкости изложения.

В этом сочинении, в частности, вводятся, независимо от китайской математики, десятичные дроби. Открытие десятичных дробей не было замечено и в должной мере оценено ни другими арабскими учеными, ни учеными Западной Европы, поэтому европейским математикам позднее пришлось открывать их заново. Сам ал-Каши в другой работе находил число π и записал его десятичной дробью с 17 десятичными знаками.

Из алгебраических сведений в сочинении «Ключ арифметики» отметим извлечение корней любой степени методом Горнера, формулу бинома Ньютона, таблицу биномиальных коэффициентов, треугольник Паскаля, связанный с этим таблицей, и тождество ССна котором основан треугольник, а также различные методы решения уравнений третьей и четвертой степени, главным образом, геометрические.

Геометрия. В геометрии результаты арабских ученых сравнительно скромны. Они знали верные формулы площадей и объемов (мы находим эти формулы уже в работе ал-Хорезми «Краткая книга об исчислении ал-джабра и ал-мукабалы»). Несколько ученых занимались комментированием «Начал» Евклида, при этом особым вниманием пользовалась теория параллельных. Были попытки доказательства пятого постулата. Отдельные ученые занимались вычислением площадей и объемов методами Архимеда, получив здесь некоторые новые результаты в сравнении с Архимедом.

Тригонометрия. Арабские ученые заимствовали элементы тригонометрии у индийцев. Они развивали как прямолинейную, так и сферическую тригонометрию, особенно сферическую, так как именно она в первую очередь важна для астрономии. Некоторые ученые занимались решением прямоугольных треугольников с помощью тригонометрии. Ведущая фигура здесь –Насир ад-Дин ат-Туси ( XIIIв.)Его сочинение «Трактат о полном четырехстороннике» посвящено тригонометрии. В нем впервые тригонометрия рассматривается как самостоятельная наука – наука о решении треугольников; до тех пор сведения по тригонометрии включались в качестве вспомогательного материала в книге по астрономии. Это первое полное изложение всей системы тригонометрии, доведенное до основных случаев решения косоугольных треугольников на плоскости и на сфере. Часть результатов получена самим ат-Туси.

Ученые, занимавшиеся астрономией и тригонометрией, составляли таблицы значений тригонометрических величин, прежде всего синуса. Со временем эти таблицы совершенствовались и уточнялись.

Из изложенного видно, что ученые стран ислама добились наибольших успехов в алгебре и тригонометрии, особенно сферической. Математика арабских стран оказала огромное влияние на развитие математики как на Востоке (в Индии), так и западе – в станах Западной Европы.