§ 17. Математика древней и средневековой Индии

Индия – страна с богатой историей. Первые рабовладельческие государства на территории Индии появились в I тысячелетии до н.э. Возник брахманизм - религия, для которой, в частности, характерно многобожие. В V в. н.э. она сменилась буддизмом, но в VIII в. окончательно победила брахманская религия.

В первых рабовладельческих государствах применялся общий язык – санскрит. Но позднее, когда государства, слабые экономически, раздираемые войнами и внутренними противоречиями, стали дробиться на более мелкие или превращаться в части других, более сильных государств, появилось большое количество народов, говоривших на разных языках, а санскрит сохранился только как единый язык религиозных книг брахманов и единый язык науки.

Индия почти никогда до XVII в. н.э., когда ее завоевали англичане, не была единым государством. Как и Китай, она нередко подвергались иноземным нашествиям. Чаще всего это происходило с северной Индией: ее завоевывали персы. Александр Македонский, скифы и др., а позднее, в средние века – арабы, монголы, Тимур и его потомки.

Индия издавна поддерживала экономические, культурные и научные связи со странами Запада (с Вавилоном, Грецией, Египтом, Византией, позднее – с арабскими странами) и Востока (с Китаем). Наибольшее влияние на индийскую науку оказали греческие ученые.

Арифметика. До VI в. н.э. в различных частях Индии применялись, в общем, письменные десятичные непозиционные нумерации. Первая запись по десятичной позиционной системе счисления появилась в конце VI в. Однако древнейшая запись со знаком нуля относится лишь к IX в. При этом нуль стали называть на санскрите “сунья” (пустое). Позднее арабы перевели этот термин словом “ас-сифр”. Отсюда происходит наше слово “цифра”, которое на латинском языке первоначально означало также нуль.

Обозначения цифр в различных районах Индии применялись разные и менялись со временем. Приведем запись цифр по наиболее употребительной системе – “девангари” (божественное письмо) (рис.28). Она сохранилась до наших дней.

Рис.28

Мы называем наши цифры арабскими. Но сами арабы называли их индийскими и заимствовали у индийцев.

Вычисления индийцы производили на счетной доске, посыпанной песком или пылью. Числа записывались заостренной палочкой.

Сложение, вычитание и, в общем, деление натуральных чисел производились способами, мало отличающимися от современных. Для умножения имелось около десятка способов. Приведем один из них.

Пример. 135 умножить на 12.

Начертим таблицу размерами 2×3 с квадратными клетками и в этих клетках проведем диагонали в одном и том же направлении (рис.29).

Число 135 запишем над таблицей, а число 12 – справа от нее по вертикали.135 умножим на 10 и результат запишем в первой строке таблицы, затем 135 умножим на 2 и произведение запишем во второй строке. Теперь производится сложение по диагоналям. ( Проверьте, например, что цифры внутри справа наклонной полосы – одного и того же разряда, а именно десятки.) Получаем ответ: 1620.

Перейдем к дробям. Индийцы знали только обыкновенные дроби и записывали их способом, мало отличающимся от современного; например, записывалось, как (без дробной черты), а смешанное число 3– как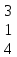. Суммаобозначалась символом, а разность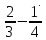– символомили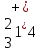

Произведение обозначалось- так же, как сложение, причем по тексту задачи или примера можно было догадаться, какое из двух действий имеется в виду. Частноеобозначалось символом.

В индийских сочинениях рассматриваются многочисленные арифметические задачи на пропорциональное деление, тройное правило ( простое и сложное), правило смешения, простые и сложные проценты и др.

2. Алгебра. Индийские математики создали алгебраическую символику, более развитую, чем у Диофанта.

Неизвестное называлось « йа» ( сокращение термина йават - тават-столько - сколько), второе, третье, четвертое неизвестное - соответственно « как», «ни», «пи» (сокращения слов калака – черный, нилака – голубой, питака – желтый), свободный член в уравнении –«ру» (рупа – целый». Сложение обозначалось знаком «йу», умножение – «гу», деление – «бха», вычитание – точкой над вычитаемым или знаком + справа от него, как в арифметике. Знак равенства отсутствует. Рассмотрим еще обозначения степеней неизвестных:

Эта символика еще не совершенна. Как и у Диофанта, используются сокращения соответствующих слов. Такая символика называется синкопированной (сокращенной, урезанной).

Другие открытия в алгебре, а также в тригонометрии и геометрии, будут рассмотрены в дальнейшем.

2. Рассмотрим работы отдельных индийских ученых по математике

Большей частью сведения по математике включались в сочинения по астрономии. Изложение математики очень лаконично и зачастую не содержит доказательств. Краткость правил порой такова, что понять их без дополнительных пояснений непосвященный читатель не мог, поэтому при обучении учитель объяснял эти правила. Кроме того, ряд сочинений написан в стихах; правила, сформулированные в коротких строках, заучивали наизусть. Преподавание, как и везде в средние века, обращалось скорее к памяти, чем к разуму.

Рассмотрим наиболее известных ученых Индии.

Ариабхата (V-VI вв.) написал сочинение по математике и геометрии, решаются линейные и квадратные уравнения. Для квадратных уравнений применяется верное правило, но находится только один корень. Неопределенное уравнение решается в натуральных числах, в отличие от Диофанта, который неопределенные уравнения решал в положительных рациональных числах.

У Ариабхаты мы находим элементы тригонометрии. Вместо хорды, как у Птолемея. он рассматривает полухорду. У него имеются следующие тригонометрические величины: синус, косинус и разность R−, причем только для острых углов. Синус назывался « ардхаджива» (полутетива); действительно, чертеж, связанный с синусом, напоминает лук с тетивой и стрелой. Позднее синус стали называть сокращенно « джива». Для индийских ученых синус и косинус зависели от радиуса окружности, поэтому вместо тождестваони пользовались тождеством

Брахмагупта (VIIв.) написал большое сочинение по астрономии « Улучшения система Брахмы». В нем две книги из 20 посвящены математике.

В этом сочинении вводятся отрицательные числа истолковываются как имущество и долг.

Квадратное уравнение приводится к стандартному виду 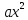=bx+c, где a

положительно, b и c могли быть и отрицательными. Формулируется правило приближенного вычисления квадратных корней.

Брахмагупта решает линейные уравнения первой степени с двумя неизвестными, более основательно, чем Ариабхата, а также уравнения второй степени с двумя неизвестными в целых числах. При этом подробно рассмотрен трудный случай – уравнение −

Итог развитию индийской математики подвел самый крупный ученый Индии Бхаскара (XIIв.). Его главное сочинение – « Венец науки», в четырех частях, две из которых посвящены астрономии, а две другие - математике. Содержание математических книг, в общем, известно из работ предшественников Бхаскары, но все это изложено более обстоятельно, в систематизированном виде. Например, подробно рассматриваются вопросы тригонометрии, приводится таблица синусов для углов через . Подробнее излагаются линейные и квадратные уравнения, решение неопределенных уравнений в целых числах. Приводятся правила вычисления площадей и объемов. Некоторые геометрические теоремы доказываются, но доказательство состоит в том, что приводится чертеж, который сопровождается словом «Смотри!». Таково, например, доказательство формулы площади треугольника. (рис. 30). Аналогично доказываются формула площади круга и теорема Пифагора.

Позднее индийские ученые нашли формулу суммы бесконечно убывающей геометрической прогрессии и разложение арктангенса в степенной ряд; последнее использовалось для уточнения числа π. Были получены разложения синуса и косинуса в степенной ряд.

Подведем итог. Главные открытия индийской математики, оказавшие большое влияние на математику Западной Европы, - создание десятичной позиционной нумерации и тригонометрии. Что касается алгебраической символики, то она не была воспринята учеными других стран, так как в ней использовались сокращения слов чуждого другим народам языка – санскрита.