§15. Древнегреческая математика после Аполлония

Со II в. до н.э. греческие города постепенно клонятся к упадку. Это связано с ослаблением экономики, полунезависимым существованием греческих городов и, главное, с завоеваниями Рима. Рим прежде всего вытеснил греков из их колоний в Южной Италии, затем захватил Сиракузы и Карфаген, в 146 г. До н.э. – всю материковую Грецию, разрушив при этом многие города, позднее – Малую Азию, в I в. до н.э. – Египет и Вавилон. Экономическая и культурная жизнь в греческих городах замерла. Для упадка в математике, кроме внешних причин, были и внутренние: отсутствие алгебраической символики и использование геометрической алгебры, что сильно усложняло доказательства и не давало возможностей для дальнейшего развития математической науки. Исследования I в. до н.э. – I в. н.э. не выходили за пределы проблем, намеченных тремя великими геометрами, - Евклидом, Архимедом и Аполлонием; например, многие ученые занимались комментированием “Начал” Евклида и составлением дополнений к этому сочинению.

Свою роль в упадке греческих городов сыграло и появление христианства. Дело в том, что постепенно христианство превратилось в Риме в господствующую религию, и церковь стала преследовать греческих ученых на том основании, что они являются язычниками. Тем не менее в первые века нашей эры Александрия остается научным и культурным центром древнего мира.

Развитие астрономии. Возникновение тригонометрии

Астрономии уделяли большое внимание многие известные математики, в том числе Евдокс и Архимед. Но были и ученые, занимавшиеся, главным образом, астрономией: Аристарх (III в. до н.э.), Гиппарх (II в. до н.э.), Менелай (I в. н.э.) и др., однако их работы почти не сохранились. Главной фигурой в античной астрономии является Птолемей.

Клавдий Птолемей (I в. н.э.) жил и работал а Александрии. Основной его труд - ”Математическое построение”. Позднее арабы дали этому сочинению другое, арабизированное название - ”Альмагест” (“Величайшая”), и под эти названием оно получило широкую известность в средние века в Западной Европе.

Сочинение Птолемея посвящено астрономии. В нем подробно излагается геоцентрическая система строения мира (позднее она получила название системы Птолемея). В частности, автору нужно было дать объяснения видимому движению Солнца, Луны и планет, солнечным и лунным затмениям и т.д., и современникам Птолемея, да и многим ученым вплоть до XVI в., эти объяснения казались вполне убедительными, хотя и трудными для понимания.

Небольшая часть “Математического построения” посвящена математике. Дело в том, что Птолемею нужно было составить таблицу координат звезд, а для этого потребовалось элементы сферической геометрии и таблица хорд окружности, соответствующих данным дугам окружности, стягиваемым этими хордами (или данным центральным углам). При составлении таблицы хорд автор широко пользуется доказанной им теоремой, которая позднее стала называться теоремой Птолемея: во вписанном в окружность четырехугольнике прямоугольник на диагоналях равен сумме прямоугольников на Противоположных сторонах (рис.25):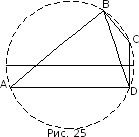

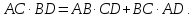(1)

Пусть во вписанном четырехугольнике является диаметром окружности, причем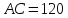(по представлениям Птолемея, радиус Вселенной постоянен; он принимает его равным некоторым 60 единицам). Соединим точки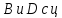ентром окружностии положим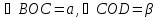(рис.26). Будем считать хорды, противолежащие этим центральным углам, известными:

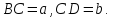
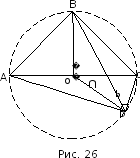
Найдем по этим данным диагональ 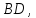т.е. хорду, противоположную углу.

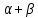Из прямоугольных треугольников

,

.

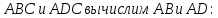
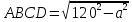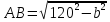Все эти данные нужно подставить в формулу (1):

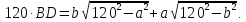
Полученный результат соответствует нашей формуле синуса суммы двух углов, только вместо хорды, противолежащей углу , да еще разделить полухорду на радиус.

Подобным же образом Птолемей находит хорду разности двух углов, хорду двойного и половинного угла.

Пользуясь формулами, выражающими стороны правильного -угольника через радиус описанной окружности при 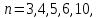он находит хорды, соответствующие центральным углам (впрочем, Птолемей пользуется дугами, которые стягиваются этими хордами) в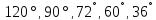. Это дает ему хорды углов

.

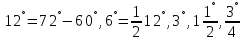Кроме того, он доказывает неравенство

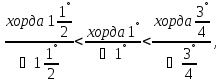
с помощью которого находит хорду 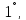а потом и хорду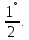

Теперь Птолемей получает хорды углов (дуг) в

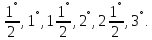
и т.д. вплоть до 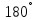. Так была составлена таблица хорд.

Конечно, таблица хорд Птолемея вместе с его правилами – это еще не основы, а начало тригонометрии. Когда в средние века индийские и арабские ученые составляли таблицу синусов, они пользовались таблицей хорд Птолемея.