§ 12. Архимед. Работа Архимеда “ Измерение круга”

В III в до н.э. греческая математика меняет свой характер. Наряду с работами по теоретической математике, характерными для IV в. до н. э., типа “Начал” Евклида, теперь начинают появляться работы по прикладной математике, связанные с вычислением площадей фигур, объемов тел, длин кривых и др. Наиболее ярким представителем этого прикладного направления в математике был Архимед.

1. Архимед Сиракузский (287-2122) родился в городе Сиракузы на острове Сицилия, где существовала греческая колония. Получил неплохое домашнее образование у отца, известного астронома. Несколько лет он провел в Александрии, где пополнил свои знания по математике и механике. Затем Архимед вернулся в Сиракузы и больше не покидал родного города.

Первые научные работы Архимеда относились к механике. Он открыл правило равновесия рычага, законы плавания тел,, изобрел т.н. “ архимедов винт” для подъема воды на поля и т.д.. Но главные его работы относятся к математике. Он написал следующие сочинения по математике: “Измерение круга”, “О спиралях”,”О ширине и цилиндре”, “О квадратуре параболы”, “О коноидах и сфероидах”, “Исчисление песчинок” и др. Почти все они относятся к геометрии. Единственная арифметическая работа –“Исчисление песчинок”. Посвящена она такой проблеме. В то время считалось, что количество песчинок на морском берегу нельзя сосчитать; действительно, в рамках применявшихся тогда ионийской системы счисления этого сделать было нельзя. Архимед изобрел новую систему счисления, которая позволяла сосчитать количество песчинок даже в том случае, если бы песком была заполнена вся Вселенная ( по представлениям того времени, в центре Вселенной находится Земля, а Солнце, планеты и звезды находятся на одном и том же расстоянии от Земли). Впрочем, для практического применения система Архимеда была непригодна.

Архимед по характеру своего творчества близок к Ньютону. Оба занимались одними и теми же науками: механикой, математикой, астрономией. Оба получили первоклассные результаты в этих областях и были знамениты при жизни.

Об Архимеде, как и о Ньютоне, рассказывали различные легенды анекдоты. Говорят, что он однажды воскликнул: “Дайте мне точку опоры и я сдвину Землю!” (Имелось в виду, конечно, использование правила равновесия рычага.) Рассказывают, что царь Сиракуз Гиерон, с которым Архимед был в дружественных отношениях, предложил ему выяснить, не подмешаны ли примеси в только что изготовленную для него золотую корону. Архимед долго думал над этим вопросом, и истина явилась ему в то время, когда он принимал ванну. Архимед выскочил из ванной и с криком “Эврика!” голый побежал по улице.

В 213 г. до н.э. во время очередной войны Рима с Карфагеном и его союзниками римские войска осадили Сиракузы. Римские войска по численности многократно превосходили войско защитников Сиракуз. Только благодаря гению Архимеда, который, не занимая никого официального поста, фактически возглавил инженерную оборону города, Сиракузам удалось продержаться около двух лет. Архимед изобрел катапульты ( метательные машины ), с помощью которых защитники города забрасывали римлян каменными ядрами, и системы блоков и рычагов для подъема ядер на городские стены. Когда римляне попытались штурмовать Сиракузы с моря, мощные краны с городских стен захватывали железными крюками носы римских кораблей, поднимая их вверх и бросали вниз; корабли переворачивались и тонули. Римлянам пришлось отказаться от штурмов города, и они перешли к долговременной осаде. В 212 г. из-за измены кого-то из горожан римские войска ворвались в город. Архимед в это время сидел у себя и чертил на песке, обдумывая очередную теорему. Внезапно перед ним появился солдат, который имел приказ доставить Архимеда к полководцу римлян Марцеллу. Архимед отказался идти до тех пор, пока не закончит доказательство теоремы. Солдат разгневался и убил Архимеда. Марцелл помог родственникам ученого его похоронить. На надгробной плите по желанию Архимеда был изображен шар, вписанный в равносторонний цилиндр (т.е. цилиндр, осевым сечением которого является квадрат), и высечена надпись о том, что отношение объема цилиндра к объему шара равно 3:2,- результат из работы “ О шаре и цилиндре”, которым Архимед гордился и с помощью которого выводил формулу объема шара.

2. Здесь мы рассмотрим сочинение Архимеда “Измерение круга”. Это сравнительно простая работа, посвященная длине окружности и площади круга. В ней изложены три теоремы.

1. Круг равен треугольнику, основание которого есть окружность, а высота – радиус:

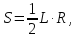
где R - радиус окружности, L – ее длина, S – площадь круга. Доказательство проводится методом исчерпывания, а следовательно, от противного.

2. Круг относится к квадрату на диаметре ( приближенно) как 11:14

,

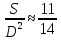где D – диаметр. Доказательство дано с помощью правильных описанных многоугольников при удвоении числа их сторон.

Интересно посмотреть, каким же было здесь для Архимеда число π. Сначала используем точную формулу площади круга:

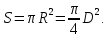
Теперь применим приближенную формулу Архимеда

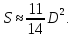
Эти два выражения приравняем. Достаточно приравнять коэффициенты при :

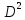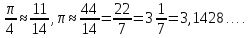
Это хорошее приближение для числа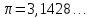. Приближенное значение π, равное 3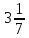, позднее получило название архимедова числа. Оно удобно тем, что здесь используется дробь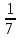с числителем, равным 1, и маленьким знаменателем.

3. Окружность превышает утроенный диаметр меньше чем на 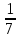и более чем на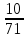диаметра:

Доказательство проводится с помощью правильных вписанных и описанных многоугольников, если число сторон принимает последовательно значение 6, 12, 24, 48, 96.

Выразим из этого неравенства отношение

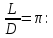
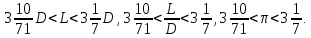
Это первая в истории оценка числа сверху и снизу. Приближенное значение π с избытком, равное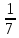 3, мы уже встречали. Приближенное значение π с недостатком, по Архимеду, равно 3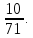Оценим его точность: 3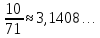. Это также хорошее приближение для π.

В дальнейшем в той же работе автор сужает границы для π, получая еще более точные значения этого числа.