
Binder1
.pdf
|
|
|
Объединяя эти результаты, получим решение неравенства в виде x 0;2 . |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
Ответ: (0; 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Пример 4. Решить уравнение |
|
x 3 2 x 3. |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
Решение. Так как |
x 3 2 |
|
x 3 |
|
|
|
, то уравнение может быть записано так: |
||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
x 3 |
|
x 3. Исходя из того, что |
|
|
x 3 |
|
|
|
x 3, при x 3, |
получим следующие |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3, при x 3, |
|
||||||||||
две системы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x |
|
3 x 3 |
|
|
|
2x |
6 |
x 3; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
а) |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x |
|
|
|
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x 3 x |
3 |
x 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Объединяя эти результаты, получим решение уравнения x 3. |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Ответ: ;3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Пример 5. Доказать неравенство: |
|
4x 1 |
|
|
|
3x 1 |
|
|
|
x |
|
. |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
Решение. Преобразуем левую часть неравенства следующим образом: |
|||||||||||||||||||||||||||||||||||||||||
|
4x 1 |
|
|
|
3x 1 x |
|
|
|
3x 1 |
|
|
|
x |
|
, что и требовалось доказать. |
|
||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
Пример 6. Решить уравнение: |
|
x 1 |
|
x2 |
2x 5. |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
x 1, x 1,
Решение. По определению x 1
x 1, x 1.
Если |
x 1, то x 1 x2 2x 5 x2 x 6 0, откуда |
x |
3, x |
|
2, |
а |
|||
|
|
|
|
|
1, |
2 |
|
|
|
удовлетворяет условиям лишь x 2, т.к. x 3 ;1 . Аналогично, если x 1, |
то |
||||||||
x 1 x2 |
2x 5 x2 3x 4 0, а x 1, x |
2 |
4. Так как |
x |
1 1; |
|
, значит |
||
|
1 |
|
1 |
|
|
|
|
||
решением является лишь x 4. |
|
|
|
|
|
|
|
|
|
Ответ: 2;4 . |
|
|
|
|
|
|
|
|
|
Пример 7. - окрестность числа x0 5 |
при 0,2 записывается (4,8; 5,2). |
||||||||
15
|
|
|
Пример 8. |
окрестность |
числа |
x0 3 |
|
при |
|
0,01 |
имеет вид |
|||||||||||||||||||||||
(-3,01; -2,99). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Пример 9. |
Интервал (1; 1,4) является окрестностью числа |
x0 1,2, а |
|||||||||||||||||||||||||||||
0,2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачи для самостоятельной работы |
|
|
|||||||||||||||||
Решить неравенства: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
10. |
|
2x 1 |
|
|
|
|
3. |
|
Ответ: 2;1 . |
|
|
1 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
11. |
|
5x 3 |
|
2. |
|
Ответ: ; 1 |
|
; |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
5 |
. |
|
||||||||||||||||||||||||||||
12. |
|
4x 1 |
|
|
|
|
|
3. |
|
Ответ: |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
;1 . |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x 3 2 9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
13. |
|
Ответ: 6;0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
14. |
|
|
3x 1 |
|
5 . |
|
Ответ: |
|
|
|
|
|
|
|
|
|
11 |
|
|
9 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
x 2 |
|
|
; |
2 |
|
8 |
; . |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
x 3 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
15. |
|
|
|
|
|
|
|
|
|
2 . |
|
Ответ: |
|
|
|
; |
|
|
|
|
|
|
; |
|
|
. |
|
|||||||
|
|
2x 1 |
|
3 |
|
2 |
|
5 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||
16. |
|
5x 1 |
|
|
|
|
|
x 2 |
|
0 . |
Ответ: |
|
|
3 |
; |
1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
4 |
6 |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
17. |
x2 |
5x 5 2 1. |
|
|
|
|
|
Ответ: 1;2 3;4 . |
||||||||||
18. |
|
|
3 x |
|
2 |
|
|
|
x 1 |
|
. |
|
|
|
|
|
Ответ: ; . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
19. |
Решить уравнение |
|
x |
|
x2 6 |
Ответ: 3;3 . |
||||||||||||
|
|
|||||||||||||||||
20. |
Записать |
- окрестность числа |
x0 , если: |
|||||||||||||||
|
|
а) x0 6, 0,2 ; |
б) |
x0 1, |
0,005. |
|||||||||||||
21. |
Задан интервал, являющийся |
- окрестностью числа x0. В ответе указать |
||||||||||||||||
x0 |
и . |
|
|
а) (0,98; 1,02); |
б) (-0,4; -0,2). |
|||||||||||||
16
§ 3. Комплексные числа. Основные понятия
Упорядоченная пара действительных чисел называется комплексным числом и обозначается z x, y , где x R e z - действительная часть числа z , y Im z мнимая часть числа z.
Число (0,1) называется мнимой единицей и обозначается i =(0,1). Множество
всех комплексных чисел обозначается символом C . |
|
|
|
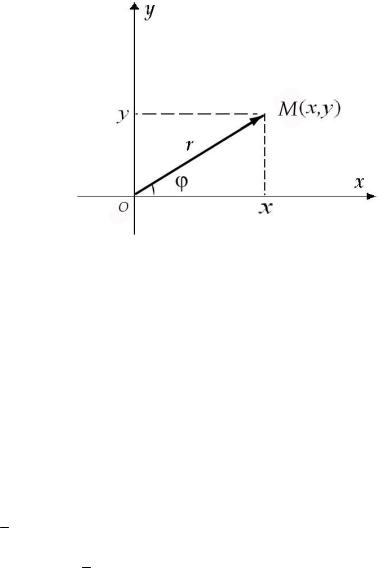
Геометрической интерпретацией комплексного числа |
z=(x,y) на плоскости |
||
|
|
|
|
в прямоугольной декартовой системе координат является |
точка M(x,y) или |
||
|
|
|
|
радиус-вектор этой точки OM (рис. 3) |
|
|
|
Рис. 3.
В этом случае плоскость называется комплексной, ось 0X – действительной осью, а ось 0Y – мнимой осью.
Алгебраическая форма комплексного числа имеет вид z x iy.
Пусть заданы z1 x1 iy1 и z2 x2 iy2 , тогда:
1)z1 z2 x1 x2 и y1 y2 ;
2)z1 z2 x1 x2 i y1 y2 ;
3)z1 z2 x1 iy1 x2 iy2 x1x2 y1 y2 i x1 y2 x2 y1 .
Число z x iy называется сопряженным числом числу z x iy, а их произведение равно z z x iy x iy x2 y2 .
17
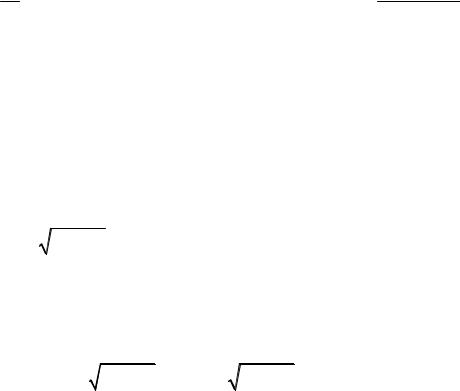
4)z1 z2
|
z1 |
|
|
|
2 |
x1 iy1 |
x2 iy2 |
|
x1x2 y1y2 |
|||||||
|
z |
|||||||||||||||
|
z |
|
|
|
|
2 |
|
x iy |
|
x iy |
|
|
|
x2 |
y2 |
|
|
2 |
z |
2 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
|
2 |
2 |
||||
Заметим, что i2 1,
i3 i2i i,
i4 i2 2 1 2 1.
i y1x2 x1y2 .
x22 y22
Тригонометрическая форма комплексного числа. Длина радиус-вектора OM
(рис.1) |
называется |
модулем |
комплексного |
числа |
и |
обозначается |
|||
|
|
|
x2 y2 .Угол |
|
|
|
|
|
|
r |
z |
|
, образованный |
вектором |
OM с |
осью |
0X называется |
||
аргументом комплексного числа |
z |
и обозначается |
arg z , причем |
||||||
положительным считают угол, измеряемый против часовой стрелки. Учитывая,
что cos |
|
|
|
x |
|
|
|
, sin |
|
y |
, |
получаем |
tg |
y |
. |
Аргумент |
z |
||||||
|
|
x2 y2 |
|
|
x2 y2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||||||
определяется |
|
|
с |
точностью до |
2 k,k Z.Главным |
значением |
arg z принято |
||||||||||||||||
считать , , а множество значений аргумента комплексного числа z |
|
||||||||||||||||||||||
Arg z arg z 2 k,k Z. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
, если x 0, |
|
|
|
|
|
|
|
|
|
|||||||
arctg |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
, если x 0, y 0, |
|
|
|
|
|
|
|
|
||||||
arctg |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
||
arg z |
arctg |
|
|
, если x |
0, y 0, |
|
|
|
|
|
|||||||||||||
|
x |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, если x 0, y 0, |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
, если x 0, y 0. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Иногда главное значение arg z рассматривается из |
0;2 . |
|
|
||||||||||||||||||||
Исходя |
из |
|
того, |
что |
x r cos , y r sin , и, |
подставляя эти значения |
в |
||||||||||||||||
алгебраическую |
форму |
комплексного |
числа, |
получаем z r cos isin , |
|||||||||||||||||||
называемое тригонометрической формой комплексного числа z .
18

Если z1 r1 cos 1 isin 1 и z2 r2 cos 2 isin 2 , то:
1) |
1 |
z |
2 |
|
1 |
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
isin |
|
|
1 |
|
|
2 |
, |
|
|||||||||
z |
|
|
|
r r |
|
cos |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2) |
z1 |
|
|
r1 |
cos |
|
|
|
|
|
isin |
|
|
|
2 |
|
, |
|
|
|
||||||||||||||||||
|
|
r |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
z |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
zn rn cos n isin n |
- эта формула называется формулой Муавра; |
||||||||||||||||||||||||||||||||||||
4) |
n z n |
|
|
|
|
2 k |
|
isin |
2 k |
|
k 0;1;2;...; n 1 . |
|||||||||||||||||||||||||||
r cos |
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
, где |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Показательная форма комплексного числа. |
Используя формулу Эйлера |
|||||||||||||||||||||||||||||||||
ei cos isin , |
получим запись комплексного числа z в показательной форме |
|||||||||||||||||||||||||||||||||||||
z rei , |
где |
r |
|
z |
|
|
- |
|
модуль комплексного числа |
z , а arg z аргумент этого |
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
числа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Пусть |
z |
|
rei 1 |
,z |
2 |
r ei 2 |
, тогда: |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1)z1 z2 r1 r2ei 1 2 ;
2)z1 r1 ei 1 2 ; z2 r2
3) zn rnein ;
4) n z n r ei |
2 k |
n , где k 0;1;2;... n 1 ; |
5) Lnz ln r i 2 k ,k z.
Выражение ln z ln r i называется главным значением логарифма.
Примеры решения задач
Пример 1. Заданы комплексные числа z1 2 3i и z2 3 i.
Найти z1 z2 , z1 z2 , z1 z2 , z1 и изобразить их на комплексной плоскости. z2
Решение. z1 z2 2 3i 3 i 2 3 i 3 1 5 2i; z1 z2 2 3i 3 i 2 3 i 3 1 1 4i;
19
z1 z2 2 3i 3 i 6 9i 2i 3i2 6 3 i 9 2 9 7i;
|
z1 |
2 3i |
|
2 3i 3 i |
3 11i |
0,3 1,1i. |
|
|
|
||||||
|
|
|
3 i |
|
|
9 1 |
|
|
|
||||||
|
z2 |
3 i 3 i |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
z1 , |
|
- число z2. Их |
|
|||
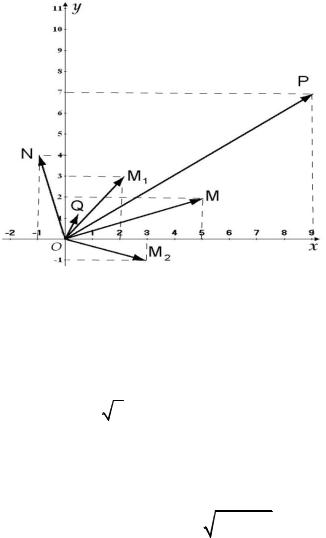
Радиус-вектор |
OM1 определяет |
число |
а OM2 |
сумма |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
OM |
OM1 |
OM2 |
а разность ON OM1 OM |
2. |
|
|
|||||||||
|
|
|
|
|
|
z1 |
|
|
|
|
|
|
|
|
|
Числа z z |
2 |
и |
изображены соответственно радиусами-векторами OP |
и OQ |
|||||||||||
|
|||||||||||||||
|
|
|
1 |
|
z2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(рис. 4).
|
Рис. 4. |
|
|
Пример 2. Заданы комплексные числа: а) z1 3, б) |
z2 3, |
в) z3 2i, |
|
г) z4 2i, д) z5 1 i, |
е) z6 3 i. |
|
|
Изобразить эти числа векторами, представить их в тригонометрической и показательной формах.
Решение. а) z 3 3 0 i, |
т.е. r 32 |
02 |
3, arctg 0 |
arctg0, так |
1 |
|
|
3 |
|
|
|
|
|
|
как радиус-вектор совпадает с направлением |
оси |
OX , то 0. Отсюда |
||
z1 3 cos0 isin 0 3ei0 (рис. 5).
20
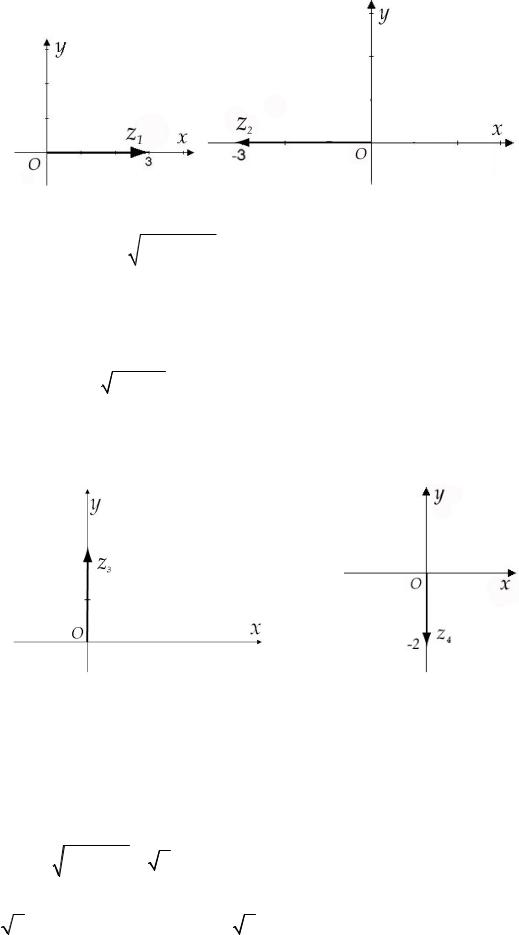
Рис. 5. |
|
|
|
|
|
|
|
|
|
|
|
Рис. 6. |
|
б) z2 3, т.е. |
|
r |
3 2 02 |
3, |
|
arctg |
0 |
arctg0, |
а радиус-вектор |
||||
|
|
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
противоположен |
направлению |
|
|
оси |
|
0X , что |
означает |
и число |
|||||
z2 3 cos isin 3ei |
(рис. 6). |
|
|
|
|
|
|
|
|||||
в) z 2i 0 2i, r 02 22 2, . |
|
|
|
|
|||||||||
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда, z3 2i 2 |
|
|
|
isin |
|
|
|
i |
|
(рис. 7). |
|
|
|
cos |
2 |
2 |
|
2e 2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Рис. 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8. |
||||
г) |
z4 2i 0 2i, находим |
|
r 2, |
|
, т.е. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
z4 |
2i 2 |
|
|
|
|
|
isin |
|
|
|
|
2e |
i |
(рис. 8). |
|
|
|||||
cos |
2 |
|
|
2 |
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
д) z5 1 i,r |
1 |
1 |
2 |
|
|
|
|
|
|
|
1 |
|
arctg 1 |
|
, |
||||||
|
2, arctg |
1 |
|
4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.е. z5 2 |
|
|
|
|
|
isin |
|
|
|
|
|
2e |
i |
|
(рис. 9). |
|
|
||||
cos |
4 |
|
|
4 |
|
4 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
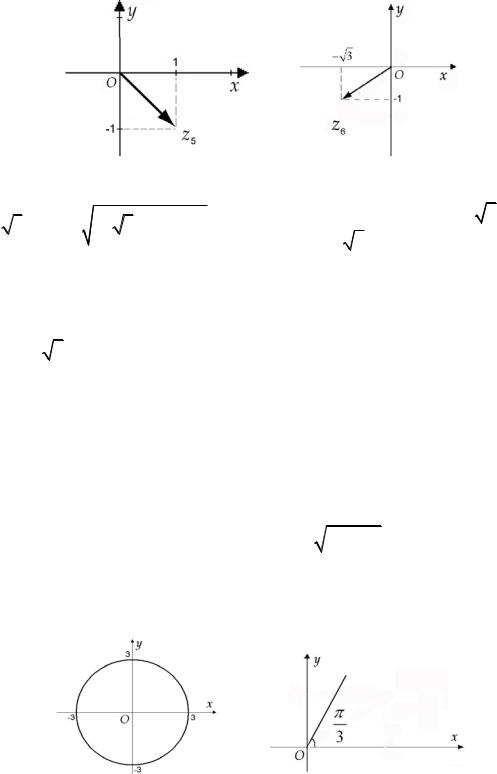
|
|
|
|
|
|
Рис. 9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10. |
|
|
|
|||||||
|
z6 3 i, r |
|
|
3 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
||||||||||||||||||
е) |
|
|
|
|
|
2, |
arctg |
|
|
|
|
|
|
|
arctg |
|
, |
с учетом |
|||||||||||||||||||||||
|
|
|
|
3 |
3 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
формулы (1), тогда |
|
5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
5 |
|
|
|
|
i |
5 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Значит, z6 3 i 2 cos |
|
|
|
|
isin |
|
|
|
|
|
|
2e |
6 |
|
|
(рис. 10). |
|
|
|
||||||||||||||||||||||
|
|
6 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Пример 3. Построить области точек z по условиям: |
|
|
|
|||||||||||||||||||||||||||||||||||
а) |
|
z |
|
3, б)arg z |
, в) |
|
z |
|
2 и |
arg z , |
г) |
|
z i |
|
1, д) Re z 1, |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
е) 0 Imz 2, ж) 1 |
|
z 3 i |
|
2. |
|
|
|
|
|
|
x2 |
y2 . Значит, строим область |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Решение. а) |
|
z |
|
3. Если z x iy, то |
|
z |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
точек, удовлетворяющих условию x2 y2 |
9, |
т.е. окружность с центром в начале |
|||||||||||||||||||||||||||||||||||||||
координат и радиусом 3 (рис. 11). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
Рис. 11. |
Рис. 12 |
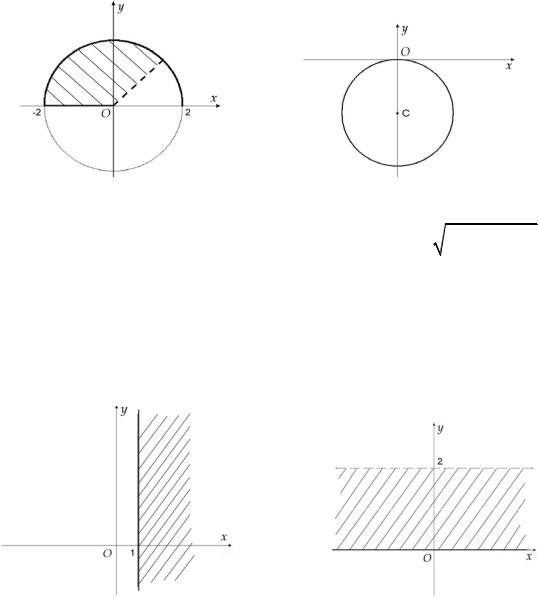
б) arg z |
|
, т.е. |
- это луч, выходящий из начала координат и образующий с |
|||
|
3 |
|
|
|
3 |
|
осью OX угол |
|
(рис. 12). |
|
|||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
22 |
в) |
|
z |
|
2 и |
|
arg z . Строим круг с центром в начале координат и радиусом 2, |
|
|
|||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
а затем лучи |
|
и , получим в качестве искомой области сектор этого |
||||
|
4 |
|
|
|
|
|
круга, ограниченный лучами |
|
и , причем луч |
|
не входит в эту |
||
|
|
|
4 |
|
4 |
|
область, а луч входит (рис. 13).
|
|
|
|
|
Рис. 13. |
|
|
|
|
|
Рис. 14. |
|
|||
г) |
|
z i |
|
1. |
Перепишем условие так: |
|
x iy i |
|
|
|
x i y 1 |
|
|
x2 y 1 2 |
1, т.е. |
|
|
|
|
|
|
||||||||||
|
|
|
|
||||||||||||
указанная область – это окружность с центром в точке C 0; 1 |
и радиусом 1 (рис. |
||||||||||||||
14). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
д) Rez 1 |
или x 1 - это полуплоскость, расположенная правее прямой |
x 1, |
|||||||||||||
включая саму прямую (рис. 15).
|
|
|
|
Рис. 15. |
Рис. 16. |
|
е) 0 ImZ 2 |
|
или 0 y 2 |
- это полоса между прямыми y 0 (ось ОХ) и |
y 2 , |
||
причем y 0 |
входит, а y 2 не входит в указанную область (рис. 16). |
|
||||
ж) 1 |
|
z 3 i |
|
2 |
23 |
|
|
|
|
||||
|
|
|
|
|
|
|

Учитывая, что z 3 i x iy 3 i x 3 i y 1 , тогда
z 3 i |
|
|
x 3 2 y 1 2 |
, условие перепишем так: 1 x 3 2 y 1 2 4 - |
|
это кольцо между окружностями с общим центром в точке C 3; 1 и радиусами 1 и 2 , причем обе окружности входят в указанную область (рис. 17).
Рис. 17
|
Пример 4. Найти 1 i |
3 6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Решение. Запишем 1 i |
3 |
в тригонометрической форме: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
r |
2 |
|
|
3 |
|
|
2 |
2, |
|
|
|
|
|
|
3 |
|
|
|
, |
1 i 3 2 |
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
arctg |
1 |
|
|
3 |
cos |
3 |
|
isin |
3 |
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
По формуле Муавра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 i |
3 |
|
6 |
|
2 |
6 |
cos |
|
|
6 |
|
isin |
|
6 |
64 |
cos 2 isin 2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
64 |
cos0 isin 0 64. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Пример 5. Найти 3 |
|
3 i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Решение. Число |
|
|
|
3 i в тригонометрической форме запишется в виде |
|
|
|||||||||||||||||||||||||||||||||
3 i |
2 |
|
|
|
|
isin |
|
|
|
т.к. r |
|
|
3 |
2 |
|
2 |
|
2, arctg |
1 |
|
|
. |
|
|
|
|
|
|||||||||||||
cos |
6 |
|
6 |
|
, |
|
|
1 |
|
|
|
6 |
Согласно |
|
|
|||||||||||||||||||||||||
|
|
|
|
3 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 k |
|
3 |
3 i 3 2 |
|
6 |
||
|
|||||
cos |
|
||||
|
|
3 |
|||
|
|
|
|
||
|
|
|
|
|
2 k
6
isin |
|
, где k 0;1;2. |
|
3 |
|||
|
|
||
|
|
|
Выпишем все три значения 3 3 i , которые получаем
24
