
Binder1
.pdf«Примеры учат лучше,чем теория» Исаак Нютон
ПРЕДИСЛОВИЕ
Предлагаемое пособие представляет собой задачник-практикум по одной из основных дисциплин высшей математики – математическому анализу и адресовано студентам технических и экономических специальностей всех форм обучения.
Цель пособия – научить студентов самостоятельно решать типовые задачи. Пособие состоит из четырех глав, каждая глава разбита на параграфы. В начале параграфа приводится минимум теоретических сведений, затем подробно разбираются типовые примеры и в конце каждого параграфа содержатся задачи для самостоятельного решения, снабженные ответами. Такая структура параграфов позволяет студентам, имеющим желание учиться, приобрести навыки решения
задач и освоить теоретический материал.
Авторы выражают искреннюю признательность профессору В.А. Головешкину за критические замечания, устранение которых способствовало улучшению пособия.
Все замечания и обнаруженные ошибки и опечатки просьба высылать по e-mail: S._V._V@hotmail.com.
Авторы
5

ГЛАВА I
ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
§ 1. Элементы теории множеств.
Основные понятия
Понятия множества, элемента множества и пустого множества в математике являются первичными, то есть исходными, неопределяемыми. Множества, как
правило, |
обозначают прописными |
буквами A, B,C, X ,Y ,..., |
а |
их элементы |
(объекты множеств) строчными буквами a,b,c, x, y,.... |
|
|
||
То, |
что элемент множества x |
принадлежит множеству |
A , |
записывается |
x A, а то, что x не принадлежит множеству A , записывается x A или x A . Пустое множество обозначается символом .
Множество может быть задано либо перечислением элементов, либо описанием свойств, характеризирующих эти элементы, при этом элементы множества записываются в фигурных скобках.
Пример 1. X a,b,c , т.е. множество X состоит из трех элементов a, b, c .
Пример 2. Запись A x : 0 x 1 означает, что множество A состоит из всех действительных чисел (если нет других условий), удовлетворяющих неравенству 0 x 1.
По числу элементов множества делятся на конечные и бесконечные, а
бесконечные множества бывают счетными и несчетными. |
|
|
|
|
|
||||||||
Множество |
X |
называется |
ограниченным, если существует такое число |
||||||||||
M 0 , что для всех элементов x X выполняется условие |
|
x |
|
M . |
|||||||||
|
|
||||||||||||
Множество |
X |
называется ограниченным сверху (снизу), |
если существует |
||||||||||
такое число M , |
что для всех |
элементов x X |
имеет место неравенство |
||||||||||
x M (или x M ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
Множество |
X называется |
неограниченным, |
если |
|
|
|
для |
любого M 0 |
|||||
существует такой элемент x0 X , что |
|
x0 |
|
M . |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
6 |
|
|
|
|
|
|
||||
Множество A называется подмножеством множества B , если каждый
элемент множества A является элементом множества |
B |
и обозначается A B |
или B A. |
|
|
Пример 3. A - множество студентов потока, |
B – |
множество студентов |
группы этого потока, тогда B A.
Множества A и B называют равными или совпадающими, если B A иA B , т.е. состоят из одних и тех же элементов и пишут A B .
Объединением (суммой) множеств A и B (обозначениеA B ) называется множество, состоящее из элементов, принадлежащих хотя бы одному из множеств A или B , т.е. A B x : x A или x B .
Пример 4. A 2,5,7 , B 3,5,6 , тогда A B 2,3,5,6,7 .
Пример 5. A 2,5,7 , B 2,5,7,8,9 , тогда A B B 2,5,7,8,9 , т.к. A B .
Пересечением (произведением) множеств A и B (обозначениеA B )
называется множество, все элементы которого являются как элементами множестваA , так и элементами множестваB , т.е. A B x : x A и x B .
Пример 6. A 2,3,4,7,9 , B 1,3,4,5,6,8 , тогда A B 3,4 .
Пример 7. A 2,3,4 , B 1,2,3,4,5 , тогдаA B A 2,3,4 , т.к. A B .
Пример 8. A 2,4,6,8 , B 1,3,5,7,9 , тогда A B .
Разностью множеств A и B (обозначение A \ B ) называется множество тех и только тех элементов множества A , которые не принадлежат множеству B , т.е.
A \ B x : x A и x B .
Пример 9. A 2,3,4,5 , B 4,5,6,7 , тогдаA \ B 2,3 .
Подмножество A называется дополнением подмножества A из множества B , если оно содержит элементы основного множества кроме элементов подмножества A , т.е. A A B, A A и A B \ A.
Пример 10. A 2,4,6 , B 1,2,3,4,5,6 . Тогда A B и A B \ A 1,3,5 .
7
Один из способов построения множества состоит в рассмотрении множеств упорядоченных пар чисел a,b . Упорядоченной называется пара чисел (а,b), где определен порядок расположения этих чисел, т.е. первым числом является а, а вторым – b. Например, пара (2;5) отлична от пары (5;2). Упорядоченные пары действительных чисел известны из школьной программы как координаты точек плоскости.
Прямым произведением множеств A и B называется множество,
состоящее из всех тех и только тех упорядоченных пар a,b , в которых a A, b B . Прямое произведение двух множеств обозначается через A B .
Таким образом, элементом прямого произведения множеств A B служит упорядоченная совокупность двух элементов, необязательно различных, элемент a считается первым элементом, b – вторым.
Пример 11. Если в десятилетней школе имеется по три класса каждого года обучения, то обозначения всех классов может быть представлено как прямое
произведение двух множеств A B , где |
A 1,2,3,4,5,6,7,8,9,10 , B а,б,в . |
|||||||||||||||||
Пример 12. Пусть A 1,2,3 , B a,1 . Тогда прямое произведение двух |
||||||||||||||||||
множеств A и B равно A B |
|
1,a |
|
|
|
|
2,a |
|
, |
|
|
|
3,a |
|
, |
|
|
. |
|
|
, 1,1 , |
|
|
|
2,1 , |
|
|
|
3,1 |
||||||||
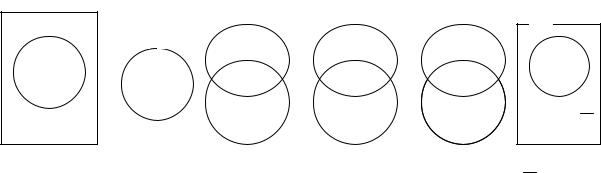
Для иллюстрации операций над множествами используют диаграммы ЭйлераВенна:
|
А В |
|
|
|
В |
|
В |
В |
В |
|
|
|
|
|
|||
В |
|
|
|
|
А |
А |
|
А |
А |
А |
A |
В А |
А = В |
А В |
А В |
А \ В |
A = В \ А |
Рис .1. Диаграммы Эйлера-Венна.
8

Для сокращения записей употребляют следующие логические символы, , … - это некоторые предложения, утверждения, высказывания. Запись означает отрицание утверждения , т.е. не ;
- квантор всеобщности, читается как каждый, любой, всякий;
- квантор существования, читается, как существует, найдется;
=> - символ импликации. Запись => означает, что из утверждения следует утверждение ; <=> - символ эквивалентности (равносильности). Запись <=> означает
утверждение эквивалентно утверждению ; : - означает «имеет место», «так, что».
Примеры решения задач
Описать следующие множества перечислением: Пример 13. Множество A x Z : x3 2x2 x 2 0 .
Решение. Рассмотрим уравнение x3 2x2 x 2 0 . Разложив левую часть на множители, получим:
x3 x2 x2 x 2x 2 x2 x 1 x x 1 2 x 1 x 1 x2 x 2
x 1 x 1 x 2 |
0 x1 1, x2 |
1, x3 |
2 . |
Так |
как |
все корни уравнения |
||
являются целыми |
числами, то множество |
A |
может |
быть записано так: |
||||
A 1,1,2 . |
|
|
|
|
|
|
|
|
Ответ: A 1,1,2 . |
|
|
|
|
|
|
|
|
|
|
Z : |
1 |
2 |
x |
|
|
|
Пример14. Множество A x |
2 |
|
3 . |
|
|
|||
|
|
|
|
|
|
|
|
|
Решение. Сначала решим неравенство 12 2x 3 1 x log2 3 .
Так как нужно рассмотреть только целые решения, то A 1,0,1 .
Ответ: A 1,0,1 .
9

Пример 15. |
|
A x R : cos2 2x 1 и 0 x 2 . |
|
|
||||||||||||
Решение. |
|
|
|
|
Решаем |
|
тригонометрическое |
|
уравнение: |
|||||||
cos2 2x 1 cos2x 1 |
2x k или |
|
x |
|
k |
, где |
k Z . |
Выбираем |
||||||||
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
значения x 0;2 и запишем |
|
|
3 |
|
|
|
|
|
||||||||
A |
, , |
|
,2 |
. |
|
|
|
|||||||||
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: A |
|
, |
, |
|
|
,2 . |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Установить какая из двух записей верна:
Пример 16. {1, 3} {1, 3, {1, 3, 5}} или {1, 3} {1, 3, {1, 3, 5}} . Ответ: {1, 3} {1, 3, {1, 3, 5}}.
Пример 17. {2, 5} {2, 5, {2, 5}} или {2, 5} {2, 5, {2, 5}}.
Ответ: обе записи верны.
Задачи для самостоятельной работы
В задачах 18-25 множества описать перечислением всех элементов
18. |
A |
|
x Z : x2 |
|
|
|
Ответ: {1, 2}. |
|
3x 2 0 . |
||||||
19. |
A |
x Z : x3 |
5x2 |
6x |
|
Ответ: {0, 2, 3}. |
|
|
0 . |
||||||
20.A x N : x 1x 2 .
21.A x N : x2 x 12 0 .
22.A x N : log0,5 1x 2 .
23.A x Z : 13 3x 4 .
|
|
3 |
|
|
|
|
|
|
|
||
24. |
A x R :sin 2x |
|
и 0 |
x 2 . |
|
2 |
|||||
|
|
|
|
||
|
|
|
|
|
Ответ: {1}.
Ответ: {1, 2, 3}.
Ответ: {1, 2, 3}.
Ответ: {-1, 0, 1}.
Ответ: , , 7 , 4 .
6 3 6 3
10
|
|
4x |
|
1 и 0 x |
|
Ответ: { /4, /2}. |
||
25. A x R : tg |
4 |
|
2 |
. |
||||
|
|
|
|
|
|
|
||
26. Описать перечислением всех элементов множества A B, A B, A \ B, B \ A ,
если A |
|
x R : x2 |
|
B |
|
x R : x2 5x 6 |
|
|
2x 8 0 , |
|
0 . |
||||
Ответ: |
A B 4,2,3 , A B 2 , A \ B 4 , B \ |
A 3 . |
|||||
27.Пусть А = [0; 3), B = (1; 5]. Найти множества А В, А В, А \ В, В \ А.
Ответ: А В = [0; 5], А В= (1; 3), А \ В= [0; 1], В \ А= [3; 5].
28.Доказать, что А В = В верно тогда и только тогда, когда В А.
Пусть В = [0; 2]. Найти дополнения следующих множеств до множества В:
29. |
A = {0; 2}. |
Ответ: |
A |
= (0; 2). |
||||
30. |
A = [1; 1,5) . |
Ответ: |
|
|
= [0; 1) [1,5; 2]. |
|||
A |
||||||||
31. |
A = (1/2; 2/3). |
Ответ: |
|
|
= [0; 1/2] [2/3; 2]. |
|||
A |
||||||||
32. |
A = {1} [3/2; 2]. |
Ответ: |
|
= [0; 1) (1; 3/2). |
||||
A |
||||||||
§ 2. Действительные числа. Числовая ось.
Абсолютная величина действительного числа. Основные понятия
Числовые множества – это множества, элементами которых являются числа. Примеры числовых множеств:
1, 2, 3... ,n,... - множество натуральных чисел;
0 0,1,2,3,...,n,... - множество целых неотрицательных чисел;
...n,..., 3, 2, 1,0,1,2,3,...,n,... - множество целых чисел;
mn :m Z ,n - множество рациональных чисел;
x : x - множество действительных чисел. Эти множества связаны между собой соотношениями: 0 .
Любое рациональное число выражается либо конечной десятичной дробью, либо бесконечной, но периодической десятичной дробью, так числа
11

15 0,2 или 23 = 0,666 … = 0,(6) являются рациональными числами.
Иррациональное число выражается бесконечной непериодической дробью:
2 1,4142356... .
Каждое действительное число изображается точкой числовой оси и, наоборот, каждой точке числовой оси соответствует единственное действительное число, т.е. устанавливается взаимно-однозначное соответствие между точками числовой оси и действительными числами.
Обозначения некоторых числовых множеств:
a,b x: a x b - интервал (открытый промежуток);
a,b x : a x b - отрезок (замкнутый промежуток);
a,b x :a x b и a,b x :a x b - полуоткрытые интервалы.
Интервалы могут быть и бесконечными, т.е. |
, a , a, , , . |
Промежуток – общее название для интервала, отрезка и полуинтервала. |
|
Абсолютной величиной (или модулем) действительного |
числа a называется |
неотрицательное действительное число, удовлетворяющее условиям:
a, еслиа 0, a a, еслиа 0.
Из определения вытекает, что a 0,a a , a a , a a . Свойства абсолютной величины:
1) x a, a 0 a x a;
x a,
2)x a, a 0
x a;
3)x y x y ;
4)x y x y ;
5)x y x y ;
6)xy  xy
xy , y 0.
, y 0.
12
Окрестностью точки на числовой оси называется любой интервал a,b , содержащий эту точку.
Проколотой окрестностью точки на числовой оси называется окрестность
точки без самой точки. |
|
|
|
|
- окрестностью точки |
x0 |
называется окрестность |
x0 |
, x0 , |
симметричная относительно точки |
x0 , |
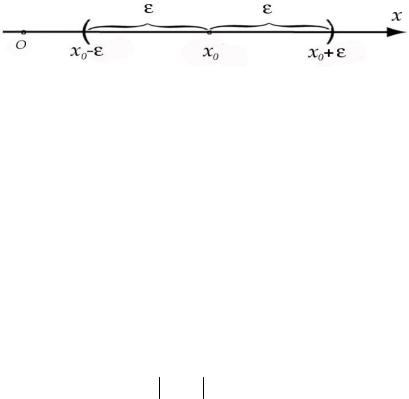
при 0. Изображение |
- |
окрестности |
точки x0 приводится на рисунке 2. |
|
|
|
|
Рис. 2 Исходя из свойств абсолютной величины действительного числа,
неравенство |
|
x |
|
|
|
перепишется x , |
то есть точка |
попадает в - |
||
|
|
|||||||||
окрестность нуля. |
|
|
|
|
|
|
||||
Неравенство |
|
x x0 |
|
означает, что |
x0 x x0 , |
то есть точка x |
||||
|
|
|||||||||
попадает в - окрестность точки x0 .
Примеры решения задач
Пример 1. Решить неравенство 5x 3 2.
Решение. |
По первому свойству абсолютной величины действительного |
||||
числа |
|
5x 3 |
|
2 |
2 5x 3 2. К каждой части этого неравенства прибавим по |
|
|
||||
3 и получим 1 5x 5 , откуда |
1 |
x |
1. |
|
|
|
|||||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Ответ |
5 |
;1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Решить неравенство |
|
|
3x |
|
1 |
|
1. |
||||
|
|
|
|||||||||
|
|
2x 1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
13

Решение. Упростим выражение под знаком модуля и неравенство
|
x 1 |
|
|
||
перепишем в виде: |
|
.Используя второе свойство абсолютных величин |
|||
2x 1 |
|||||
|
|
|
|||
действительного числа, получим
|
|
|
x 1 |
1, |
|
x 1 |
1 0 |
|||
|
|
|
|
|||||||
x 1 |
|
2x 1 |
|
|
2x 1 |
|
|
|||
1 |
|
|
|
|
||||||
|
|
|
|
|
||||||
2x 1 |
|
x 1 |
1. |
|
x 1 |
1 |
0 |
|||
|
|
|
|
|
|
|
|
|||
|
|
2x 1 |
2x 1 |
|||||||
|
|
|
|
|
|
|
||||
2 x 0
2x 1
3x 0
2x 1
Решая эти неравенства методом интервалов, получим |
|
0; |
1 |
|
|
1 |
;2 |
|
|||||||
x |
2 |
|
|
2 |
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0; |
1 |
|
|
1 |
;2 |
|
|
|
|
|
|
|
|
|
Ответ: |
2 |
|
|
2 |
. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 3. Решить неравенство: |
|
|
2x 1 |
|
|
|
x 1 |
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x 1, при x 1 |
|
|
|
|
|
|
|
||||||||
Решение. По определению |
|
|
2x 1 |
|
|
2 |
а это означает, что вся |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x 1,при x |
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
числовая ось будет разбита на следующие интервалы |
|
|
1 |
|
|
1 |
|
||||||||||||||||||||||||||||||||||||||||||||
; 1 ; 1; |
2 |
|
и |
2 |
; , |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где нужно рассматривать данное неравенство. Итак: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
а) если x ; 1 , то |
|
2x 1 |
|
|
|
|
|
x 1 |
|
|
|
2x 1 x 1 x 2 x 2, а это не |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
входит в рассматриваемый интервал; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
б) если |
x |
|
|
|
1 |
|
|
2x 1 |
|
|
|
|
x 1 |
|
2x |
1 x 1 3x 0 x 0, |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
1; |
2 |
, то |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. x |
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) если |
|
|
|
1 |
|
|
|
то |
|
2x 1 |
|
|
|
x 1 |
|
2x |
1 x 1 x 2, откуда |
следует, |
что |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
x |
2 |
; |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
;2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
решением являются |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
x |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
