
Binder1
.pdf
Вычислить пределы используя второй замечательный предел:
1. |
lim |
x 1 |
2 x 1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
3x2 |
|
|
|
|
|
|
|
|
2 x 1 |
|||||
2. |
lim |
|
|
|
|
5 |
|
|
3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
x |
|
|
3x |
2x |
1 |
|
|||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
3x 4 |
|
|
x 1 |
|
|
|
|
|
|||||||
3. |
lim |
|
|
|
3 |
|
|
|
|
|
|||||||||
|
|
3x 2 |
|
|
|
|
|
|
|
|
|
|
|||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4. |
lim |
|
|
3x 4 |
x 1 |
|
|
|
|||||||||||
|
|
6x 1 |
|
|
|
|
|
|
|||||||||||
x |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 2x |
|
|
3x 1 |
|
|
|
|||||||||
5. |
lim |
|
|
|
4 |
|
|
|
|
|
|||||||||
|
|
5 2x |
|
|
|
|
|
|
|
|
|
||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||
11. |
lim |
|
x2 |
2x 1 |
x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
4x |
2 |
|
|||||||||||
|
x x |
|
|
||||||||||||||||
12. lim 1 2x |
2 |
|
ctg2 x |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
13. |
lim |
ln 1 3x |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
x 0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||
14. |
lim |
ln x 2 ln 2 |
|
||||||||||||||||
|
|
||||||||||||||||||
|
x 0 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||
15. |
lim |
x a x c |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x x b |
|
|
|
|
|
|
|
|||||||||||
Ответ: e4 .
Ответ: e 94 .
Ответ: e 23 .
Ответ: 0.
Ответ: e 32 .
Ответ: e2 .
Ответ: e2 .
Ответ: 3 .
Ответ: 12 .
Ответ: ea b .
1
6. lim 2 cosx sin2 x
x 0
1
7. lim x x 2 x 2 2
|
1 3x |
x 1 |
|
4 |
|
||
8. lim |
|
||
x |
5 3x |
||
9. lim 2 sin x 3tg2 x
x
2
3x2
10. lim 1 sin2 x ctg 4
x 0
|
|
|
|
x 3 |
|
|
1 |
|
|
|
|
sin |
x 3 |
||||
16. lim |
|
2 |
e |
4 |
|
|
|
|
|
2 |
|||||||
|
|
|||||||
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. lim cos x ctg5x2
x 0
1
18. lim tgx 4 x
x
4
1
19. lim 1 sin2 x x 2
x
Ответ: e .
Ответ: e .
1
Ответ: e3 .
3
Ответ: e2 .
4
Ответ: e3 .
Ответ: e 12 .
Ответ: e 101 .
Ответ: e .
Ответ: 1e .
95
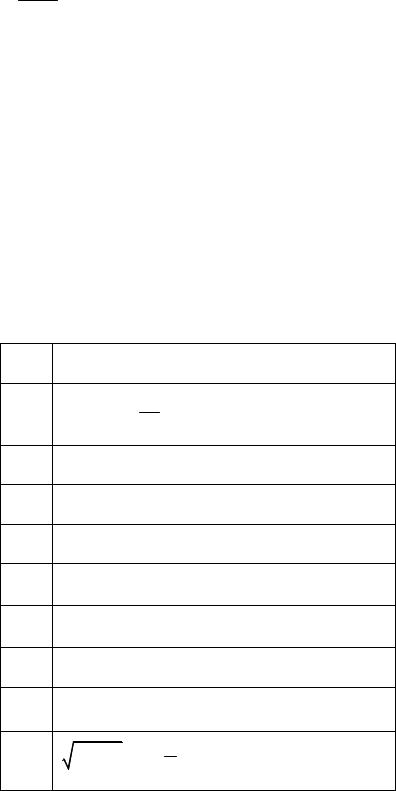
Бесконечно малые функции
Определение 1.
Пусть (x) и (x) - две бесконечно малые функции при x a.
1. Функция (x) называется бесконечно малой более высокого порядка при x a ,
чем (x) , если limx a ((xx)) 0.
Принято обозначение o( ) при x a ( равно «o малое» от при x a ).
2. Функции |
(x) и (x) называются бесконечно малыми одного порядка при |
|||
x a , если предельное значение функции |
(x) |
в точке а существует и отлично |
||
(x) |
||||
от нуля: lim |
(x) |
c 0. |
|
|
|
|
|
||
x a |
(x) |
|
|
|
3. Функции (x) и (x) называются эквивалентными бесконечно малыми при
(x)
xa , если предельное значение функции (x) в точке а равно единице.
При x 0 имеют место следующие асимптотические формулы:
1.sin x x o x
2.cos x 1 x22 o x2
3.tgx x o x
4.arcsin x x o x
5.arctgx x o x
6.ex 1 x o x
7.ax 1 x ln a o x
8.ln 1 x x o x
9.1 x n 1 nx o x
10.n 1 x 1 nx o x
96

|
Пример 1. Верно ли равенство (x) o(x2 ) |
при x 0 , если: |
|
|
|
||||||||||||||||||||||||||||
а) (x) 1 cos 2x ; б) (x) x3 ; в) (x) tg2 x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а) 1 cos 2x o x2 , так как |
lim |
1 cos 2x |
lim |
2 sin 2 x |
|
|
|
|
sin x |
2 |
|||||||||||||||||||||||
|
|
x |
2 |
|
|
|
x |
2 |
|
|
2 lim |
x |
|
2. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|||||||
Функции 1 cos 2x и x2 |
- бесконечно малые одного порядка в точке x 0 . |
||||||||||||||||||||||||||||||||
б) |
x3 |
o(x2 ) |
|
lim |
x3 |
lim x 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
, так как x 0 |
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x 2 |
|
|
|||
|
|
|
|
|
|
|
tg 2 x |
|
|
|
sin x |
2 |
|
|
1 |
|
|
|
lim |
x |
|
|
|
|
|||||||||
|
|
|
x o x |
|
, так как |
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
||||||||||||
в) tg |
2 |
2 |
lim |
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
||||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|||||||||||||||||||
|
|
x 0 |
x |
|
|
x 0 |
|
x |
|
|
|
cos |
x |
|
|
lim cos |
x |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
Функции tg2 x и x2 - эквивалентные бесконечно малые в точке x 0 . |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
sin x x2 x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Пример 2. Вычислить lim |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
3x x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Запишем асимптотические разложения числителя и знаменателя при x 0 .
Пользуясь асимптотической формулой для синуса и определения символа «o малое», получаем:
sin x x2 x3 x o(x) x2 x3 x o(x) , 3x x4 3x o(x).
|
|
sin x x2 x3 |
|
x o(x) |
|
1 |
o(x) |
|||||
|
|
|
|
x |
|
|||||||
Таким образом |
lim |
|
lim |
|
|
|
lim |
|
|
|
|
|
3x x4 |
3x |
o(x) |
|
|
o(x) |
|||||||
x 0 |
|
x 0 |
x 0 |
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
x |
|||
Пример 3. Вычислить lim |
3 x3 |
2x4 |
. |
|
|
|
|
|
|
|||
ln(1 |
2x) |
|
|
|
|
|
|
|||||
|
|
x 0 |
|
|
|
|
|
|
|
|||
|
1 lim |
o(x) |
|
|
1 |
|
x |
||||
|
x 0 |
||||
|
|
|
|
3 . |
|
3 lim |
o x |
||||
|
x |
|
|||
|
x 0 |
|
|||
Решение. Найдем асимптотическое разложение числителя, используя формулу
(1 x) 1 x o(x) :
3 x3 2x4 x 1 2x 13 x |
1 |
2 x o(x) |
x 2 x2 o(x2 ) x o(x). |
|
|
|
3 |
|
3 |
|
|
|
||
Здесь мы воспользовались тем, что x o(x) o(x2 ) , 23 x2 o(x2 ) o(x).
Пользуясь также асимптотическим разложением логарифма ln(1 2x) 2x o(x) , находим:
97

|
3 x3 2x4 |
|
x o x |
|
|
1 |
o(x) |
|
|
1 . |
||||
lim |
lim |
lim |
|
x |
|
|
|
|||||||
ln(1 2x) |
|
|
|
|
o(x) |
|
||||||||
x 0 |
x 0 |
2x o(x) |
x 0 |
2 |
|
|
|
2 |
||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|||
|
Пример 4. Вычислить lim |
ex2 cos x |
. |
|
|
|
|
|||||||
|
x |
2 |
|
|
|
|
|
|
||||||
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|||
Решение. Используя асимптотическую формулу 6 при y x2 и формулу 2 для косинуса, получаем:
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
x |
2 |
|
|
|
3x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
o(x |
2 |
|
|
|
o(x |
2 |
|
o(x |
2 |
) |
|
||||
lim e |
x2 |
cos x |
|
|
|
|
|
|
) 1 |
2 |
|
) |
2 |
|
|
||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|||||||||
|
x2 |
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
x2 |
|
|
||||||||
x 0 |
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|||||
|
|
3 |
|
|
2 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
o(x |
|
3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x 0 |
|
x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Здесь мы воспользовались тем, что o( ) o( ) o( ).
1
Пример 5. Вычислить limx 0 (cos x) sin 2 x .
Решение. Данный предел является неопределенностью типа 1 .
lncosx
Запишем cos x 12 в виде e sin2 x .
sin x
|
|
1 |
lim ln cos x |
|
Тогда |
lim |
cos x |
|
ex 0 sin2 x . |
sin2 x |
||||
|
x 0 |
|
|
|
Для вычисления предела в показателе экспоненты воспользуемся асимптотическими разложениями для функций ln cos x и (sin x)2 при x 0 :
(sin x)2 x o(x) 2 |
x2 2x o(x) o(x) 2 |
x2 o(x2 ) o(x2 ) |
|
|||||||||||||||||||||
x2 |
o(x2 ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
2 |
|
|
|
|
x2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
o(x ) |
|
|
|
|
o(x ). |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ln cos x ln 1 |
2 |
|
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При получении первого из этих равенств мы также учли, что o(x) n |
o(xn ) |
|||||||||||||||||||||||
n N , |
x o(x) o(x2 ) , o(x2 ) o(x2 ) o(x2 ) , c o(x) o(x) c 0. |
|
||||||||||||||||||||||
Таким образом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ln cos x |
|
|
|
|
x2 |
o(x |
2 |
) |
|
|
1 |
|
|
1 |
|
||||||||
lim |
lim |
|
2 |
|
|
|
, а исходный предел равен e |
|
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
|
||||||||
|
sin |
x |
|
x |
2 |
o(x |
2 |
) |
|
2 |
|
|||||||||||||
x 0 |
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|||||||||||
98

|
|
|
|
Задачи для самостоятельной работы |
|
Вычислить пределы, используя приведенные в таблице 1 асимптотики |
|||
простейших функций: |
|
|||
1. lim |
|
sin 5x |
. |
Ответ: 5 . |
|
|
|||
x 0 ln 1 3x |
|
3 |
||
2. |
lim 1 cos 2x . |
|
|
|
|
|
|
|
|||||||
|
x 0 1 cos |
x |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||
3. |
lim |
|
ln cos x |
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||||||||
|
x 0 |
|
4 1 x2 1 |
|
|
|
|
|
|
|
|||||
4. |
lim |
|
sin 3x arcsin2 x arctgx2 |
||||||||||||
|
|
|
|
|
|
3x |
|
. |
|||||||
|
x 0 |
|
|
|
|
|
|
|
|
||||||
5. |
lim |
|
5tgx x2 x3 |
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
5x4 |
||||
|
x 0 sin 2x 2sin2 x |
|
|||||||||||||
6. |
lim |
ln 1 tg4x |
. |
|
|
|
|
||||||||
|
|
|
|
|
|||||||||||
|
x 0 |
|
esin 2x 1 |
|
|
|
|
|
|
|
|||||
7. |
lim |
|
etg3x 1 |
|
|
|
|
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x 0 ln 1 sin 2x |
|
|
|
|||||||||||
8. |
lim |
|
sin 5x |
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x 0 x4 x2 x |
|
|
|
|
|
|
|
|||||||
9. |
lim |
arcsin x 1 |
. |
|
|
|
|||||||||
|
|
|
|
||||||||||||
|
x 1 |
|
x2 5x 4 |
|
|
|
|
|
|
|
|||||
ln 1 2x 3x2 4x3 10. lim .
x 0 ln 1 x 2x2 x3
Ответ: 36.
Ответ: 2 .
Ответ: 1.
Ответ: 2,5.
Ответ: 2.
Ответ: 1,5.
Ответ: 5.
Ответ: 13 .
Ответ: 2 .
99

ГЛАВА III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
§1. Вычисление производных с использованием таблицы
иосновные формулы дифференцирования. Производная обратной функции
1.Определение производной. Пусть функция y f x определена в некоторой
окрестности точки x . |
|
|
10. Приращением функции y f x в точке |
x , |
соответствующим приращению |
аргумента x , называется функция аргумента x |
|
|
y f x x f x . |
(1) |
|
20. Отношение приращения y функции |
в |
точке x к соответствующему |
приращению аргумента x x 0 называется разностным отношением
|
y |
f |
x x f x |
. |
|
||
|
|
|
|||||
|
x |
|
x |
|
|
|
|
30. Производной функции y f x в точке x |
называется предел при |
||||||
разностного отношения (если он существует): |
|
|
|
||||
dy |
y ' f ' x lim |
y |
lim |
f x x f x |
|
||
x |
|
x |
|||||
dx |
x 0 |
x 0 |
|
||||
Операция нахождения производной называется дифференцированием.
2.Производные простейших элементарных функций. (Таблица)
1)(x )' x 1 ( - любое число);
2)(sin x)' cos x ;
3)(cos x)' sin x ;
4)(tgx)' cos12 x ;
5)(ctgx)' sin12 x ;
(2)
x 0
(3)
6) (arcsin x)' |
1 |
; |
|
1 x2 |
|||
|
|
100

7) (arccos x)' |
|
|
|
|
1 |
|
; |
|
|
||||||||
|
1 x2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
8) |
(arctgx)' |
|
|
1 |
|
|
; |
|
|
|
|
|
|||||
1 |
x2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
9) |
(arcctgx)' |
|
|
1 |
|
|
; |
|
|
|
|||||||
1 |
x2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
10) |
(ax )' ax ln a , в частности, ex ' ex ; |
|
|
||||||||||||||
11) |
(loga x)' |
|
1 |
|
|
|
( a 0, a 1; x 0 ), в частности, ln x ' |
1 |
; |
||||||||
x ln a |
x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
12)(shx)' chx ;
13)(chx)' shx ;
14)(thx)' ch12 x ;
15)(cthx)' sh12 x .
Здесь |
sh x, ch x, th x, cth x - гиперболические функции, которые определяются |
||
следующими формулами: |
|||
sh x |
ex e x |
- гиперболический синус; |
|
2 |
|||
|
|
||
ch x |
ex e x |
- гиперболический косинус «цепная линия»; |
|
2 |
|||
|
|
||
th x |
sh x |
|
ex e x |
||||
ch x |
ex e x |
||||||
|
|
|
|||||
cth x |
ch x |
|
ex e x |
||||
sh x |
ex e x |
||||||
|
|
|
|
||||
-гиперболический тангенс;
-гиперболический котангенс.
3. Основные правила нахождения производной.
Если каждая из функций u u x и v v x дифференцируема в точке x , а c,c1 и c2 - постоянные величины, то
1) c1u c2v ' c1u ' c2v ',
101
2) |
uv ' u 'v v 'u , |
|
(4) |
|||||
3) |
u |
' |
u 'v v 'u |
v x 0 |
|
|||
|
|
|
|
|||||
v2 |
||||||||
|
v |
|
|
|
||||
4)c ' 0, cu ' cu '.
4.Производная обратной функции.
Теорема: Если функция y f x строго монотонна и непрерывна в некоторой окрестности точки x , имеет производную в точке x и f ' x 0 , то существует обратная функция x f 1 y , которая определена в некоторой окрестности точки y f x и имеет производную в точке y , причем
|
x'y |
1 |
(5) |
|
yx' |
||
|
|
|
|
|
Примеры решения задач |
||
Пример 1. Пользуясь определением производной, найти производную |
|||
функции y x2 |
в точке x 1. |
|
|
Решение. Найдем приращение функции y x2 в точке x 1, соответствующее приращению аргумента x :
y f 1 x f 1 1 x 2 1 2 x x 2 .
Составляем разностное отношение
xy 2 x .
По определению
y ' 1 lim |
y |
|
lim |
2 x 2 . |
x 0 |
x |
|
x 0 |
|
Пример 2. Пользуясь определением найти производную функции y sin x . Решение. Фиксируем x и составляем разностное отношение:
|
|
|
|
2sin |
x |
|
x |
||
y |
|
sin x x sin x |
|
2 |
cos x |
2 |
|
||
|
|
|
|
|
. |
||||
x |
x |
|
|
x |
|
|
|||
|
|
|
|
|
|
|
|||
102
Для вычисления производной функции y sin x в точке x надо найти предел:
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||
|
y |
|
|
|
|
|
|
|
x |
sin |
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
lim |
|
|
|
lim |
cos x |
|
|
|
|
|
|
. |
|
|
(1) |
||||
x |
|
2 |
|
x |
|
|
|
|
|||||||||||
x 0 |
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как функция y cos x является непрерывной x , то |
|||||||||||||||||||
|
|
|
|
x |
cos x . |
|
|
|
|
|
|
|
|
|
(2) |
||||
lim cos x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Далее, согласно первому замечательному пределу |
|||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
sin |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim |
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
(3) |
||||
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С учетом (2) – (3) из (1) следует: |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||
|
y |
|
|
|
|
|
|
|
x |
|
|
sin |
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||
lim |
|
|
lim |
cos x |
|
|
|
lim |
|
cos x, |
|||||||||
x |
2 |
|
x |
|
|||||||||||||||
x 0 |
|
x 0 |
|
|
|
x 0 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.е. sin x ' cos x . |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Пример |
|
3. |
Используя |
определение |
вычислить производную функции |
|||||||||||||
y loga x 0 a 1 .
Решение. Фиксируем x и составим разностное отношение, считая x x 0 :
y |
|
loga x x loga x |
|
1 |
|
|
x |
|
1 |
|
x |
|
|
x |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
loga 1 |
|
|
|
|
loga 1 |
|
|
|||||||
x |
|
|
|
|
x |
|
x |
x |
x |
x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
loga 1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Согласно второму замечательному пределу |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
x |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
103

при любом фиксированном x 0 . Тогда, с учетом |
непрерывности функции |
||||
y loga x в точке x e получаем: |
|
||||
loga x ' |
loga e |
|
1 |
. |
|
|
x ln a |
|
|||
|
x |
|
|
||
Пример 4. Используя правило дифференцирования обратной функции, |
|||||
вычислить производную функции y arcsin x . |
|
||||
Функция y arcsin x является обратной для функции |
x sin y , определенной на |
||||
интервале 2 y 2 .
Пользуясь правилом дифференцирования обратной функции, получаем
yx' |
1 |
|
1 |
|
1 |
|
|
1 |
|
, |
||||
|
cos y |
1 sin2 y |
|
|
||||||||||
|
x'y |
|
|
|
|
1 x2 |
|
|||||||
где учтено, что cos y 0 на |
|
|
|
, |
|
|
|
|||||||
|
2 |
2 |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, arcsin x ' |
|
|
|
1 |
|
|
|
x 1, 1 . |
||||||
|
1 x2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример 5. Вычислить производную показательной функции y ax 0 a 1 . |
|||||||||||||
Решение. |
Показательная функция |
y ax определена на бесконечной прямой и |
||||||||||||
является обратной для логарифмической функции x loga y , определенной на прямой y 0 .
Согласно теореме о производной обратной функции справедлива формула
ax |
' |
|
1 |
|
|
|
|
1 |
x |
|
' |
|
|
|
|||
|
|
loga |
y y |
|
1 |
|||
|
|
|
|
|
loga e |
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
y |
|
|
|
y |
|
ax ln a . |
|
1 |
|
||
|
|
|
|
|
|
|
|
||
|
ln a |
|
||
Итак, ax ' ax ln a |
x . |
Пример 6. Вычислите производную функции y xsinlnxx .
Решение. Пользуясь правилами дифференцирования произведения и частного и таблицей производных, получаем
104
