Binder1

Найти наименьшее и наибольшее значение функций на указанных отрезках (30-34):

30. y 2x3 9x2 12x 2 на отрезке 1;3 .

Ответ: y 2 2 - наименьшее значение, y 3 7 - наибольшее значение.

31. y x4 8x2 3 на 2;2 .

34. y x2 4 на 6;8 .

Ответ: y 2 y 2 0 - наименьшее значение, y 8 60 - наибольшее значение.

35. Найти наименьшее значение функции y lnxx .

Ответ: y e e .

36. Найти наибольшее значение функции y x1 ln x .

Ответ: y e 4 e .

37. Доказать, что из всех прямоугольников, имеющих данную площадь a2 , квадрат имеет наименьший периметр.

155

38. Сумма двух неотрицательных чисел x y 6 . Найти наибольшее значение x5 y .

Ответ: 3125.

39. Из трех досок одинаковой ширины сколачивается желоб. При каком угле наклона боковых стенок площадь поперечного сечения желоба будет наибольшей?

Ответ: 3 .

40. Требуется изготовить закрытый цилиндрический бак объемом V . Какими должны быть его размеры, чтобы на его изготовление ушло наименьшее количество материала?

Ответ: R 3 2V , H 2R .

41. На гиперболе x2 y2 1 найти точку, ближайшую к точке 3;0 . 2

Ответ: 2;1 и 2; 1 .

§ 4. Вогнутость, выпуклость функции и точки перегиба. Асимптоты графика функции.

Исследование функции и построение графика функции. Основные понятия

Функция y f x называется выпуклой (вогнутой) на интервале a,b , если ее график расположен ниже (выше) любой своей касательной на этом интервале.

интервале выпуклая, если f '' x 0, то функция – вогнутая.

Точкой перегиба называется такая точка графика, в которой существует касательная, и в окрестности которой график функции лежит по разные стороны касательной, т.е. точка перегиба отделяет выпуклую часть графика от вогнутой.

156

Достаточное условие существования перегиба. Если вторая производная непрерывной функции y f x меняет знак при переходе через критическую точку x0 , то эта точка будет точкой перегиба графика функции.

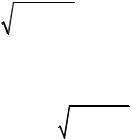
Асимптотой графика функции y f x называется прямая, обладающая тем свойством, что расстояние от переменной точки на графике до этой прямой стремится к нулю при неограниченном удалении этой точки по графику от начала координат.

Асимптоты могут быть вертикальными, горизонтальными и наклонными. Вертикальные асимптоты – это прямые параллельные оси ОY. Пусть при

асимптотой.

157

Для полного исследования функции и построения ее графика может быть предложена следующая схема:

1.Найти область определения функции. Определить точки разрыва функции, выяснить их характер и найти интервалы непрерывности функции.

2.Проверить является ли функция четной, нечетной, периодической.

3.Найти точки пересечения графика функции с осями координат, интервалы знакопостоянства.

4.Найти асимптоты графика функции.

5.Вычислить первую производную функции. Найти экстремумы функции

ипромежутки ее возрастания и убывания (интервалы монотонности).

6.Вычислить вторую производную функции. Найти точки перегиба и интервалы выпуклости и вогнутости графика функции.

7.Контрольные точки, т.е. уточнение значений функции в отдельных, вызывающих сомнение, точках.

8.По результатам исследования построить график функции.

При решении конкретной задачи отдельные этапы этой схемы могут быть расширены, другие же могут оказаться излишними или невыполнимыми.

Указанную схему следует рассматривать как сугубо примерную. В частности, эскиз графика рекомендуется набрасывать уже после нахождения асимптот (если они имеются) и, во всяком случае, до нахождения точек перегиба. Однако следует помнить, что основными ориентирами при построении графика функции являются точки кривой, соответствующие экстремальным значениям функции, точки перегиба, асимптоты.

Примеры решения задач

Пример 1. Найти сумму абсцисс точек перегиба графика функции y x5 5x4 203 x3 3x 3.

Решение. Найдем производные: y ' 5x4 20x3 20x2 3, y '' 20x3 60x2 40x 20x x2 3x 2 20x x 1 x 2 .

158

Из того, что y '' 0 при x1 0, x2 1, x3 2 и по знаку второй производной определим промежутки выпуклости и вогнутости графика функции. Оформим это в виде следующей таблицы:

Из таблицы видим, что вторая производная меняет знак при переходе через каждую критическую точку, поэтому все эти точки являются точками перегиба графика функции. Сумма их абсцисс равна 0 1 2 3 .

Ответ: 3.

Пример 2. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции y 3 5 x 2 7 .

Решение. Находим производные:

Вторая производная не обращается в нуль ни в одной точке из области определения, а при x 2 она не существует. Так как функция всюду определена, то x 2 - критическая точка. Составим таблицу:

Точка 2;3 - точка перегиба.

159

Пример 3. Найти уравнение асимптоты к графику функции

160

Уравнение наклонной асимптоты при x y x . Таким образом, график функции y x arctgx имеет две различные наклонные асимптоты:

y x при x ,т.е. правую и y x при x , т.е. левую.

Пример 5. Методами дифференциального исчисления провести полное исследование функции и построить ее график:

y 1 x3x2 .

Решение.

Найдем эти точки: 1 x2 0 x 1.

Следовательно, областью определения данной функции является вся

Установим характер разрыва функции в этих точках, вычисляя

161

Y совпали, то есть график функции проходит через начало координат.

Функция может изменить свой знак лишь при переходе через такие точки, в которых она равна нулю или имеет точку разрыва. Чтобы определить знак функции в любом интервале знакопостоянства, достаточно вычислить ее значение в любой

Следовательно, исследуемая функция положительна в интервале (0;1). Аналогично исследуются знаки функции в остальных интервалах. Результаты удобно свести в таблицу.

4) Односторонние пределы функции при x 1 бесконечны, значит, прямые x 1 являются вертикальными асимптотами.

Ищем наклонные асимптоты:

Уравнение наклонной асимптоты имеет вид y x .

162

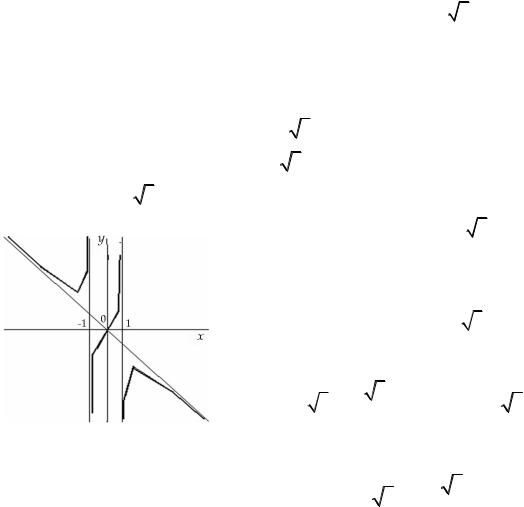
С этого момента на черновике можно начинать строить схему графика. Нанесем точки пересечения с осями координат, асимптоты и поведение функций около асимптот (рис. 42).

Найдем производную функции:

Рис. 42.

Определим интервалы знакопостоянства производной, они же интервалы возрастания и убывания функции.

Интервалы знакопостоянства производной определяются по той же схеме, что и

интервалов. Как и ранее определяем знак производной в каждом интервале. По знаку производной делаем вывод о характере поведения функции в интервале (возрастание или убывание). Результаты удобно свести в таблицу. В таблице знакуказывает на возрастание функции, знак - на убывание.

163

Точками экстремума могут быть только те точки, в которых производная или равна нулю или не существует, т.е. x 1, x 0 , x 3 . В точкахx 1, x 1 функция не определена, а значит, они не могут быть точками экстремума.

При переходе через точку x 0 знак производной не изменяется, а значит, она также не является точкой экстремума.

При переходе через точку x 3 производная меняет свой знак с минуса на

С учетом проведенного исследования уже может быть построен схематичный график (рис. 43).

6)Находим вторую производную:

Находим нули и точки разрыва второй производной, интервалы выпуклости и вогнутости функции.

Вторая производная равна нулю только в одной точке x 0 , имеет точку разрыва в точках x 1.

Как и в предыдущем случае определяем интервалы знакопостоянства, и по знаку второй производной делаем вывод о выпуклости или вогнутости функции.

164