Ovru-all

числу станів з даною енергією. Ламана лінія символізує випадкове блукання в просторі конфігурацій при послідовних змінах однієї з координат, що характеризують мікростан системи, згідно з вищеназваними алгоритмами. Ця ламана найчастіше проходить через найвигідніші з ентропійно-енергетичної точки зору макростани (не дуже велика енергія і велика кількість мікростанів з такою енергією – мінімальній енергії відповідає тільки один мікростан й відповідно нульова ентропія). При цьому більшість конфігурацій макроскопічної системи взагалі не реалізується. Тому середні значення фізичних величин можна обчислити з використанням лише тих конфігурацій, які були реалізовані в результаті випадкового блукання в процесі моделювання. Чим довше відбувається це блукання, тобто чим більше воно захопило конфігурацій (або, як зазвичай кажуть, чим краще набрана статистика), тим точніше будуть обчислення.

1.2.3. Алгоритм Метрополіса й алгоритм термостата

Метод Метрополіса був сформульований в його роботі з розрахунку рівняння стану рідини, що складається з твердих дисків [8]. Сутність методу полягає в генерації набору послідовних конфігурацій системи. На кожному кроці цього процесу за наявною попередньою конфігурацією будується наступна, що відрізняється від попередньої зміною одного зі ступенів вільності. Нова конфігурація може бути прийнята або не прийнята в ансамбль у відповідності до процедури статистичного випробування. Якщо за результатом статистичного випробування нова конфігурація відкинута, то в ансамбль на даному кроці ще раз включається попередня конфігурація. Таким чином, в залежності від важливості, вага даної конфігурації в ансамблі може зростати.

Визначивши спосіб блукання фазовим простором системи, необхідно задати імовірності переходу між двома конфігураціями на даному кроці блукання. При цьому треба виходити з того міркування, що в граничному випадку великого числа блукань система переходить у рівноважний стан. Це означає, що середнє від будь-якої фізичної величини A за Марковим часом обчислюється за формулою

N

<A>N=(1/N) ∑ A(ti ) . (1.13)

i=1

де ti – i-й момент (крок) часу, в який зроблено вимірювання величини A, в граничному випадку великого числа N вимірювань має пере-

21

ваного стану, а при «гарячому» (спіни в початковій конфігурації спрямовані випадковим чином) – до невпорядкованого.

Застосування алгоритму Метрополіса до ансамблю систем, які складаються з двох спінів та термостату, призводить до зміни кіль-

костей систем у можливих конфігураціях N−−, N−↓, N↓− і N↓↓ у напрямку їх рівноважних значень, що відповідають канонічному роз-

поділу: N−↓/N−−=N−↓/N↓↓=N↓−/N−−=N↓−/N↓↓=ехр(–2J).

Згідно з алгоритмом Метрополіса, імовірності переходів

р(−−→−↓)=р(−−→↓−)=р(↓↓→−↓)=р (↓↓→↓−)=ехр(–2J); (1.15) р (−↓→−−)=р (−↓→↓↓)=р (↓−→−−)=р (↓−→↓↓)=1. (1.16)

Зміна числа систем N−↓ за один Марковів крок за рахунок переходів −↓→−− та −−→−↓ складатиме

N−↓=n−↓→−−–n−−→−↓=N−−(N−↓/N−−–exp(–2J)). (1.17)

Якщо, наприклад, число систем N−↓ більше рівноважного значення (більше відношення N−↓/N−−), то частіше відбуватимуться переходи −↓→−−, тобто число систем N−↓ буде зменшуватись, доки відношення N−↓/N−− не відповідатиме Гіббсовим вагам ( N−↓=0). Якщо ж відно-

шення N−↓/N−− менше рівноважного, буде більше переходів −−→−↓, що призведе ансамбль до правильних співвідношень між кількостями систем.

Практично, при чисельному моделюванні ми зазвичай маємо один Марковів ланцюг. Зазначений ансамбль систем можна замінити досить довгими «часовими» відрізками цього ланцюга. Середнє від будь-якої величини за ансамблем таких відрізків і є середнє за Марковим часом. Цей доказ легко переноситься на будь-яку іншу систему з дискретними або безперервними ступенями вільності.

У алгоритмі термостату [9] на кожному кроці часу Маркова один зі ступенів вільності приводиться у теплову рівновагу із зовнішнім «термостатом», що має певну температуру Т, при цьому враховується взаємодія з іншими (фіксованими на даному кроці) ступенями вільності. Внаслідок багаторазового повторення такої процедури для всіх ступенів вільності за досить довгий час Маркова настає повна термодинамічна рівновага всієї системи з термостатом. Наприклад, в моделі Ізінга на кожному кроці положення чергового спіна обирається з імовірністю, що визначається лише температурою термостата і конфігурацією сусідніх спінів. Нормовані імовірності станів з енер-

23

ви. В цьому разі за кожним із напрямків у гратці перший і останній ступені вільності в даному ряді взаємодіють так, неначе вони сусіди. Таким чином, за кожним з напрямків гратка замикається в кільце (вона утворює тор відповідної розмірності).

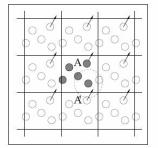
Як можна бачити з рис. 1.3,а, атом А0 взаємодіє не тільки з атомом А з основної області, що розглядається, а й з уявним атомом А’, зміщеним відносно А на період ідентичності. Якщо ж атом А знаходиться в лівій нижній чверті, його образ А’ визначається зсувом на період за двома напрямками (рис. 1.3,б)

Рис. 1.3. Схема взаємодій приграничного атома.

У разі, коли частинки можуть переміщуватися, зазвичай використовують наступні періодичні граничні умови. Якщо в результаті зміни координат частинка А виходить за межі кубічної області через певну грань, то через протилежну грань буде введена частинка, А’, котра зветься "образом". При цьому введена частинка буде займати в об'ємі куба місцеположення, координати якого обчислюють за формулою:

де і - декартовий індекс (і=1,2,3), хА – координата частинки після зсуву, х'А – координата "образу", L – лінійний розмір комірки. Таким же чином перетворюються інші координати. У результаті замість частинки вводиться її образ з тим самим номером. Загальна кількість частинок в системі при цьому не змінюється. Введення "образу" продемонстровано на рис. 1.4. Таким чином, кожна частинка після зсуву опиняється в основній кубічній комірці із частинок, оточеній комірками з "образів". Це компенсує вплив границь при обчисленні енергії взаємодії.

25

Перевагою періодичних граничних умов є те, що всі ступені вільності стають рівноправними. Область МК моделювання "вбудовується" у середовище, при цьому усуваються небажані поверхні i створюється квазінескінченний об’єм, який дозволяє розглядати основну комірку як елемент нескінченної системи. Проте періодичні крайові умови можуть наводити (і дійсно наводять) значний додатковий порядок у конденсованих системах. Періодичні граничні умови є доцільними, якщо в певному напрямку модельної схеми можна виявити період повної ідентичності, що дозволяє імітувати нескінченну протяжність речовини (кристала) в розглянутому напрямку. У разі багатофазних систем їх застосовують у напрямках, де немає міжфазних меж. Треба також мати на увазі, що поява кристалічного зародку поблизу періодичної межі миттєво ініціює його ріст з протилежного боку.

Рис. 1.4. Пересування частинки та її образів при застосуванні

періодичних граничних умов,

у сферу обрізання включаються як частинки з основної комірки, так і їхні образи.

Наразі, коли персональні комп’ютери дозволяють моделювати системи у сотні тисяч атомів, є змога зовсім не застосовувати періодичні умови, а розглядати системи з вільними поверхнями, або застосовувати періодичні умови тільки за одним або двома напрямками. Системи з відкритою поверхнею краще відповідають реальним системам у разі вивчення фазових переходів. При досить великих розмірах системи вплив меж на значення екстенсивних (тобто тих, що залежать від розміру системи) фізичних величин незначний, оскільки частка поверхневих атомів мала. У багатьох випадках вибір правильних крайових умов може стати вирішальним для усього експерименту.

26

1.2.5. Вибір потенціалу взаємодії атомів

Питання ви6оpу потенціалу взаємодії є суттєвим при моделюванні атомної структури речовини. Вибір потенціалу має залежати від типу зв'язків в конкретній речовині, фізичних уявлень про природу взаємодії частинок у ній.

Потенціали обчислюють у різні способи. Теоретичні потенціали, розраховані за законами квантової механіки, враховують розподіли густини зарядів (електронної густини) [10]. Емпіричні потенціали розраховують на основі експериментальних даних щодо дифракційних досліджень структури речовини (структурного фактору, парної функції радіального розподілу атомів) [11]. Ті та інші потенціали корегують, аби результати моделювання відображали фізичні властивості відповідної речовини, такі як: пружні сталі, температурну залежність коефіцієнту розширення, температуру плавлення, теплоємність. Задовольнити всі ці вимоги вдається далеко не завжди. І твердження про те, що потенціал відноситься саме до цієї речовини, не завжди є обґрунтованим. Особливу цінність мають дослідження, які виражають загальні закономірності тих чи інших фізичних процесів, так що неточності потенціалів не змінюють характер процесів, що відбуваються.

Залежно від природи речовини, що моделюється, використовують парні, тричастинкові та багаточастинкові потенціали. У випадку останніх потенціальна енергія системи є функцією не тільки відстаней до атомів, що оточують розглядуваний атом, а й від їх координат (кутів, які вони утворюють з розглядуваним атомом). У разі парних потенціалів враховуються тільки відстані між атомами. Результат їх застосування відповідає дійсності, якщо енергія взаємодії двох частинок не залежить від розташування інших частинок. Така ситуація має місце для простих рідин та аморфних речовин, для різних станів металів. Тричастинкові потенціали застосовують до описів систем з ковалентними зв’язками. Багаточастинкові потенціали корисні для описів більш складних систем, наприклад, твердих тіл з дефектами структури. У найпростішому випадку взаємодія частинок може бути парною. При цьому енергія взаємодії системи:

де ri – координата i-ї частинки, rij – відстань між i-ю та j-ю частинками.

27